Il rovesciamento della prassi

S'è creduto di danzare sulle spoglie del determinismo di Laplace. Ma il caso è un concetto del tutto negativo, vuoto, e dunque spoglio di interesse scientifico. Il determinismo, invece, è un oggetto di affascinante ricchezza, per quanti sappiano esaminarlo (René Thom, Basta con il caso, taccia il rumore).

Il lettore attento che, scorrendo il testo di Bordiga Teoria e azione nella dottrina marxista del 1951, giunga alla sintetica spiegazione dello schema sulla successione delle forme di produzione, non mancherà di stupirsi alla lettura di quelle poche righe. Due schemi sono messi a confronto: quello che rappresenta la concezione gradualistica delle variazioni storiche, a forma sinusoidale continua, e quello della concezione rivoluzionaria che invece rappresenta i rapporti di produzione come fasi spezzate (vedi figura più avanti). La differenza fra i due schemi viene così spiegata:

"La prima curva o curva degli opportunisti (...) è una curva continua che in tutti i punti 'ammette una tangente', ossia praticamente procede per variazioni impercettibili di intensità e di direzione. La seconda curva, con cui si è voluta dare una immagine semplificatrice della tanto deprecata 'teoria delle catastrofi', presenta ad ogni epoca delle punte che in geometria si chiamano 'cuspidi' o 'punti singolari'. In tali punti la continuità geometrica, e dunque la gradualità storica, sparisce, la curva 'non ha tangente' o, anche, 'ammette tutte le tangenti' − come nella settimana che Lenin non volle lasciar passare".

Il commento di questo passo richiederebbe ben più spazio di quanto qui ci sia concesso, ma ci accontenteremo dell'essenziale. "Teoria delle catastrofi" oggi evoca unicamente il lavoro di René Thom che va sotto quel nome e che in realtà l'autore ha chiamato, con espressione meno giornalistica e assai significativa, Stabilità strutturale e morfogenesi. Nel 1951 non potevano essere conosciuti neanche gli stadi iniziali di tale lavoro e tantomeno il nome dato alla teoria, che è successivo alla sua pubblicazione (1972; in italiano sarà pubblicato da Einaudi solo nel 1980).

Bordiga si riferisce quindi alla "tanto deprecata" teoria del catastrofismo rivoluzionario, che risale a Marx ed Engels, ma che è mutuata da Hegel, il quale studiò dal punto di vista filosofico il passaggio repentino delle forme o degli stati in fisica. Il mutamento continuo della temperatura dell'acqua è un mutamento quantitativo che non cambia la natura dell'acqua, perché essa conserva le sue proprietà non misurabili, cioè le sue qualità. Ma l'acqua ad un certo punto diventa ghiaccio o vapore. Se ci si attiene all'apparenza del fenomeno, il mutamento qualitativo, che è un salto, una rottura di continuità, non sembra avere relazione con il mutamento quantitativo. Invece, conclude Hegel, la relazione c'è (oggi diremmo che gli atomi sono sempre gli stessi). Marx utilizza l'argomento per dimostrare il salto qualitativo dal denaro, esistente da millenni, al valore-Capitale, fenomeno recente, e cita direttamente Hegel. Engels riprende il discorso nell' Antidühring (Il Capitale, libro I, cap. IX. Antidühring, Prima sezione cap. XXII).

Il lettore stupito si è già tranquillizzato dopo essersi dato questa prima spiegazione, quando subito dopo l'inciso deve ricredersi: c'è effettivamente la descrizione, ridotta all'osso, della teoria delle catastrofi di Thom. Per quanto la coincidenza sembri sensazionale, essa è invece del tutto "normale": Bordiga non è un "vate" che anticipa di oltre vent'anni la scoperta, ma un utilizzatore di scoperte borghesi a fine rivoluzionario. La definizione coincide perché in ogni caso la scelta delle parole non poteva essere vasta più di tanto. Ma coincide anche il succo della teoria perché essa scaturisce da scoperte che "erano nell'aria" e che Thom riuscì a formalizzare. Bordiga doveva conoscere gli antecedenti della teoria delle catastrofi perché risalgono ai primi trent'anni del secolo e, tra gli altri, troviamo all'origine del percorso anche Poincaré, ispiratore di Thom.

La moderna teoria delle catastrofi è per noi interessante perché mette in discussione una volta di più il dualismo tra quantitativo e qualitativo e in fondo si colloca positivamente nel grande filone della nostra teoria della conoscenza. Inoltre è perfettamente inserita nei "sistemi" deterministici, quindi è uno strumento in più per combattere le teorie del dubbio e dell'indeterminato. Infine, è in grado di descrivere una classe di fenomeni molto ampia: praticamente qualunque transizione discontinua che si verifichi in un sistema che sia composto da due o più stati stabili. In senso dinamico essa spiega un sistema che possa seguire più di un percorso stabile di trasformazione. Un esempio un po' rozzo ma efficace può essere quello di una biglia che si muove su un piano (stato stabile) e finisce per cadere (catastrofe) su un altro. La catastrofe propriamente detta è quindi il passaggio repentino da uno stato all'altro o da un percorso all'altro (anche un asse che si spezza sotto un peso crescente è una catastrofe). Si incomincia a capire che la questione ha molta attinenza con la struttura dei cambiamenti sociali: da una situazione stabile, cambiamenti continui e impercettibili portano alla rottura discontinua, al salto rivoluzionario in un'altra forma sociale.

I sistemi viventi, che sono i più restii a lasciarsi formalizzare e sono visibilmente non-statici, si possono anche definire in "equilibrio dinamico", frase che a prima vista sembra una contraddizione. In effetti, sia gli organismi individuali che la società di individui, assorbono e trasformano continuamente energia. Nessuno stato all'interno di tali sistemi può essere stabile, ma l'insieme degli stati resiste straordinariamente alle perturbazioni perché ogni stato interagisce con l'altro annullando gli effetti a cascata di eventi singolari. Il diagramma delle successive forme di produzione (cuspidi, vedi figura) ideato da Bordiga offre la visione d'insieme delle successive transizioni di stato, ma la visione "fine" del processo non è spiegata. Tale spiegazione dettagliata compare nel diagramma del "rovesciamento della prassi" (vedi più avanti), anche qui posto in relazione ad altri diagrammi che schematizzano le varie concezioni opportunistiche. Per evidenziare quanto sia aderente lo schema di Bordiga alle moderne formalizzazioni della complessità − teoria delle catastrofi, matematica del caos, frattali, biforcazioni ecc. − metteremo a confronto due procedimenti in antitesi, il primo di Ilya Prigogine (indeterminista), il secondo di René Thom (determinista).

Nell'esempio di Prigogine alla figura (a), per un dato valore (l ') del parametro di controllo l , il sistema può assumere, alla biforcazione B, tre diversi stati stazionari: C, E, D. Due di questi sono stabili, mentre uno è instabile. Al variare del parametro di controllo l possiamo seguire a piacere il percorso A,B,C sulla figura. Al contrario, al variare di X, fermo rimanendo il parametro di controllo l , si giunge al punto D. In ogni caso, lo stato che si raggiunge dipende dalla precedente storia del sistema. Questo tipo di determinismo è stato provato sia in colture biologiche, sia in concentrazioni chimiche. Prigogine osserva:

"Finora la storia era stata adoperata, normalmente, per l'interpretazione dei fenomeni biologici o sociali. Che essa possa giocare lo stesso importante ruolo in elementari processi chimici, è piuttosto sorprendente" (Ilya Prigogine e Isabelle Stengers, La nuova alleanza, Cap. quinto, 6: "Biforcazioni e rotture di simmetria", Einaudi 1981).

Ma nella figura (b) Prigogine osserva che ora il diagramma di biforcazione, a differenza del precedente, presenta due soluzioni simmetriche e stabili

"Dove andrà il sistema quando arriva al punto di biforcazione?" si chiede. "C'è qui una scelta fra due possibilità (...) come farà il sistema a scegliere fra destra e sinistra? Siamo di fronte ad un elemento irriducibilmente casuale".

Ogni sistema, aggiunge l'autore, posto di fronte a biforcazioni multiple (a cascata) in cui è indecidibile la "scelta" (e già avremmo da dire sul termine) fra diversi possibili futuri, rappresenta una transizione al caos. Dalla commistione fra caos e necessità, in presenza di piccole perturbazioni del sistema, può nascere un nuovo ordine. Questa è la stessa conclusione a cui giunge Jacques Monod nel suo celebre saggio Il caso e la necessità (Arnoldo Mondadori, 1970. Su questo saggio è disponibile una nostra critica: "Comment Mr. Monod terrasse la dialectique", Programme communiste n. 58, aprile 1973).

Nella teoria di René Thom, il punto di partenza per la rappresentazione della "catastrofe" più semplice, assomiglia molto ad un diagramma di biforcazione in cui uno degli assi è il solito fattore di controllo e l'altro è il comportamento generale del sistema verso un "massimo" o un "minimo".

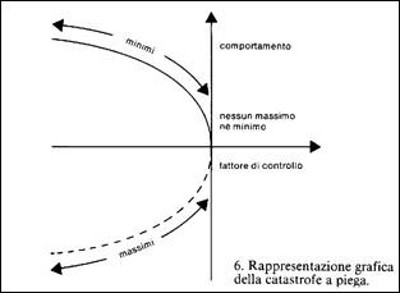
Il comportamento qualitativo di tale sistema è molto semplice. Per certi valori del fattore di controllo esistono sia massimi che minimi e il sistema è stabile con una attrazione verso i minimi. Ad un valore critico del fattore di controllo il sistema assume un equilibrio incerto, mentre al di là del valore critico diventa completamente instabile. Questo modello contiene troppo poca informazione per essere esplicativo di fatti reali, ma serve per capire il meccanismo della teoria: tutto dipende dal fattore di controllo. Thom aggiunse che quello degli indeterministi è un trucco volgare, perché nessun sistema presenta tratti isolati corrispondenti a un diagramma di biforcazione perfettamente simmetrico. Ogni "storia" dei singoli percorsi possibili è in relazione con l'universo delle storie adiacenti; e il fatto stesso che l'indecidibilità venga risolta con una ricerca statistica dei risultati dimostra che vi è una regolarità statistica, quindi un substrato deterministico. Nella dinamica dei fatti sociali la "teoria delle catastrofi" come la intendeva Bordiga ha più fattori di controllo (lo vedremo fra poco), ma il semplice diagramma di biforcazione simmetrica ad un solo fattore di controllo è sufficiente per fare alcune considerazioni in rapporto alla teoria marxista del partito.

Thom, criticando Prigogine, non escluse affatto che la dinamica dei sistemi complessi contenesse dei punti singolari che conducono alle biforcazioni; o, se la biforcazione è impercorribile, alla "catastrofe". Solo che

"Il gioco intellettuale dei teorici del caos dall'ordine e dell'ordine dal caos, cioè del caso e della necessità, è consistito nel cancellare mentalmente l'ambiente dinamico globale - sempre deducibile da un esame sufficientemente completo della base su cui il sistema si sviluppa - a vantaggio della piccola perturbazione scatenante cui segue il crollo della stabilità imperfetta del sistema verso un equilibrio di energia inferiore. L'artificio sta nel far credere che l'evoluzione successiva, dagli effetti spettacolari, sia effettivamente creata dalla 'fluttuazione' scatenante. (...) Un esame sufficientemente completo della base su cui il sistema si sviluppa permette di prevedere a priori i possibili esiti della biforcazione, che preesiste alla fluttuazione scatenante. Spetta a quest'ultima il ruolo di innescare il processo ed eventualmente di determinare, con una scelta apparentemente arbitraria, fra tutti gli esiti possibili l'ulteriore evoluzione. Ma certo non la crea".

Ci scusiamo con l'autore per aver modificato un pochino il linguaggio eccessivamente tecnico a favore di chi legge. Nella dinamica rivoluzionaria formalizzata da Bordiga con lo schema del rovesciamento della prassi, abbiamo: 1) una analisi della base su cui il sistema si sviluppa in cui si individuano 2) quattro "parametri di controllo" la cui dinamica porta 3) a una biforcazione indecidibile (continuazione del capitalismo o rovina di tutte le classi) per cui si presentano tutte le tangenti o nessuna tangente sulla cuspide (la settimana che Lenin non volle lasciar passare) e quindi 4) si rovescia la prassi perché il partito, prodotto della storia, ne diventa fattore soggettivo, rappresentando la "volontà".

Nella teoria delle catastrofi di Bordiga i quattro parametri di controllo (vedi figura) sono rappresentati in uno schema a due dimensioni, mentre nella teoria di Thom sarebbero rappresentati in quello che viene chiamato "grafico di catastrofe a farfalla" che si svolge in uno spazio a più dimensioni. Lo schema di Bordiga dimostra che, in prossimità della biforcazione, nella polemica tra Prigogine e Thom, ebbe ragione Thom: l'ambiente, l'universo delle determinazioni da cui nessun atomo sociale può sottrarsi, essendo polarizzato dalla convergenza di interessi che contrappongono non più individui ma blocchi interi della società, classi, porta lo strumento partito a scegliere. E qui il termine non ha più quel senso di "libero arbitrio" che Prigogine assegna ai fenomeni dinamici. Non sappiamo se Thom fosse anticomunista come tutti i suoi colleghi dediti alla scienza pagata dalle università borghesi, ma il cervello sociale ha il sopravvento su quello individuale del ricercatore, e questo è un duraturo insegnamento proprio di Bordiga. Del resto proprio Thom registrò il fenomeno quasi con le stesse parole di Bordiga:

"Molte acquisizioni della scienza sono indubbiamente vere, ma il loro interesse è debole, quasi nullo. Il vero problema è rintracciare la fonte dell'interesse. In alcuni casi si tratta di una fonte sociologica locale: un risultato è interessante semplicemente perché il finanziatore della ricerca ha sottoposto allo scienziato un problema che questi ha tutto l'interesse di risolvere, se non altro per fare carriera".

Ma vi sono alcuni casi in cui la ricerca rientra nel bisogno di conoscenza globale, che è il vero scopo, quello che serve per "decifrare il mondo, renderlo intelligibile"; allora l'interesse non è più venale, perché "svelare una struttura soggiacente che renda i fenomeni intelligibili" significa adottare quel metodo dell'astrazione che, dedotto da Hegel, Marx ha potentemente mutuato e rovesciato, e che Bordiga rivendica in ogni sua riunione, in ogni suo scritto sui problemi della conoscenza. Sostituire un visibile complesso con un invisibile semplice (astratto) non è problema di interpretazione della realtà, ma di rivelazione della realtà.

L'impresa di rivelare la struttura soggiacente della società capitalistica, che contiene in sé tutti gli invarianti delle precedenti società, sembrerebbe un compito impossibile al pari dell'impresa di ordinare in qualche schema l'infinità dei movimenti e dei cambiamenti propri dell'intero mondo che ci circonda. Bordiga ha letto Leibnitz e la sua "legge di continuità" (1687) che prevede un certo ordine nelle domande per avere un ordine nelle risposte; ha studiato certamente i risultati delle ricerche di Poincaré e seguito il dibattito sulla stabilità del sistema solare (P. es. Duhem, 1914), da cui si ricava che il problema delle perturbazioni che portano alle "catastrofi" in fondo è il problema della validità del determinismo.

La fatidica domanda cui rispondere è: se un sistema dinamico subìsce perturbazioni continue e tende matematicamente ad ampliarle fino a che piccole variazioni iniziali producono grandi cambiamenti finali, come mai, praticamente, la maggior parte delle forme (compreso il capitalismo) rivela una robustezza insospettata rispetto alle piccole perturbazioni? Per rispondere secondo il linguaggio "catastrofista" diremo: esiste una stabilità strutturale insensibile a singoli elementi critici, ma nello stesso tempo essa è messa in discussione da perturbazioni che, in fasi del tutto determinate, possono portare a rotture discontinue. La comprensione dei fenomeni è resa possibile dalla loro riduzione tramite processi di astrazione.

La teoria delle catastrofi ha provocato adesioni e critiche, ma una cosa ha dimostrato: l'impresa, un tempo disperata, di dare spiegazione al numero infinito di forme e comportamenti si dimostra fattibile dato che, sottoponendo tali forme e comportamenti ad alcuni vincoli, alla fine se ne trova un numero finito di tipi, secondo Thom e i suoi allievi soltanto sette.

Nello schema di Bordiga è anche spiegata la genesi di teorie borghesi che avanzano parallelamente al marxismo ed in ritardo rispetto ad esso. Le determinazioni che salgono dalle spinte fisiologiche elementari dell'individuo verso l'attività cosciente dell'organizzazione, si invertono: l'attività cosciente dell'organizzazione determina il comportamento delle classi e l'azione degli individui, mentre l'influenza rivoluzionaria neutralizza l'influenza conservatrice e consente il salto sociale. Prima che succeda questo salto, è inevitabile che i bisogni reali della produzione e della ricerca producano molte di queste capitolazioni ideologiche borghesi di fronte al marxismo.

Poiché ogni schema di catastrofe (dei sette tipi possibili) deve rispondere al "vincolo di Leibniz" sopra ricordato, la ricerca intorno alla discontinuità nei sistemi dinamici non può assumere la discontinuità stessa come dato della dinamica. I ricercatori che hanno lavorato sulla ricchezza potenziale della teoria di Thom hanno osservato che il concetto di "spiegazione" implicito nella teoria è rilevante anche sotto il profilo della tecnica matematica perché la pone nel grande filone classico della ricerca sul "continuo". Se questa interpretazione è corretta, e se Bordiga fosse vissuto abbastanza per venirne a conoscenza, tutto ciò gli sarebbe piaciuto assai. Scrive infatti nel 1956 a proposito della teoria della relatività (sottolineatura nel testo):

"Sostituito il tempo locale al tempo universale si può riscrivere la meccanica con formule nuove, ma sugli stessi principii di Galileo, di Newton, di d'Alembert, con le stesse equazioni canoniche... [Einstein] lascia ferma l'ipotesi di Cartesio e di Leibniz, ossia tutto misura con grandezze variabili gradualmente, dunque continue, applicando quindi il calcolo infinitesimale e i sistemi di coordinate [anche se] chiede tuttavia alle matematiche nuovi apparati" (Relatività e determinismo cit.).

Questa rivendicazione di una "scienza del continuo" è importante perché contribuisce ad avvicinare la scienza alla concezione unitaria dell'universo che è propria del marxismo. Einstein, aggiunge Bordiga, scrive "alla fine, la identità monistica e materialistica tra materia e pensiero". Come farebbe chiunque si trovasse a marciare sulla nostra stessa strada.

La concezione teorica "catastrofica" marxista espressa dallo schema del rovesciamento della prassi disegnato da Bordiga unisce in un rapporto dialettico il "substrato", cioè l'ambiente economico materiale che è l'arena delle relazioni umane, con gli effetti dell'ideologia e del "pensiero". L'azione del partito politico, che è sovrastruttura, diventa, al punto di catastrofe, forza materiale che provoca un cambiamento qualitativo di "stato".

"Il rapporto dialettico sta nel fatto che in tanto il partito rivoluzionario è un fattore cosciente e volontario degli eventi, in quanto è anche un risultato di essi e del conflitto che essi contengono fra antiche forme di produzione e nuove forze produttive. Tale funzione teorica ed attiva del partito cadrebbe però se si troncassero i suoi legami materiali con l'apporto dell'ambiente sociale, della primordiale, materiale e fisica lotta di classe" (Teoria e azione nella dottrina marxista cit.).

Alla luce di queste citazioni risulta più chiara una celebre quanto perentoria affermazione di Bordiga: le rivoluzioni e i partiti non si fanno, si dirigono (in "Partito e azione di classe", Rassegna comunista, 1921).

Un divulgatore scientifico che ha redatto un saggio sulla teoria delle catastrofi, pur non badando al rapporto dialettico fra il partito e l'ambiente che lo rende "prodotto e fattore di storia", è colpito dall'atteggiamento di Lenin nell'Ottobre, quando si presentò "la settimana da non lasciar passare". Tale autore registra a suo modo, un po' ingenuamente, la forza sovvertitrice del rovesciamento della prassi operato dal partito bolscevico:

"Durante gli eventi che condussero alla rivoluzione russa, si dice che Lenin fosse molto attento alla tempestività delle mosse dei bolscevichi per giungere al potere. Nelle circostanze adatte, disse, basterà una piccola 'spinta' per provocare una transizione che in un altro momento richiederebbe uno sforzo molto maggiore" (A. Woodstock e M. Davis, La teoria delle catastrofi, Garzanti 1982).

Eravamo partiti da una considerazione di Bordiga sullo stesso fatto: è interessante ritrovarla in un libro sulla teoria matematica delle catastrofi.

Rivista n. 19