3. La scienza della rivoluzione

Tre formule per l'invarianza

Abbiamo già visto che nella riunione di Milano del 7 settembre 1952 compare un sottotitolo con la parola invarianza tra virgolette. Questa forma grafica sarebbe ingiustificata se non si volesse dare un significato particolare al testo, come si trattasse di una citazione, un riferimento a questioni conosciute. In effetti il termine invariante è utilizzato in molte discipline scientifiche anche se in accezioni un po' diverse.

Una definizione possibile è: "Proprietà di sistema chimico-fisico in equilibrio che si ha quando non è possibile far variare alcuno dei parametri che lo caratterizzano senza alterare tale equilibrio".[1]

In senso stretto Bordiga, nel testo citato, usa il termine in questa prima accezione: non è possibile variare una parte che compone il tutto senza che l'intera costruzione crolli. Questo vale anche nel tempo, perciò il marxismo è invariante dato che nasce da fattori che sono sempre gli stessi finché esisterà la società divisa in classi (invarianza storica).

Un'altra definizione, più strutturata, è la seguente:

"Proprietà di una legge, sistema, corpo, figura, di restare immutati sebbene varino degli stessi valori le grandezze in essi contenute. Proprietà essenziale sia per la formulazione delle leggi razionali (in matematica) sia per la formulazione delle leggi naturali (in fisica), che sarebbero altrimenti del tutto improponibili"[2].

In questa seconda definizione, che comprende la precedente, abbiamo la descrizione di un importante elemento della topologia, la possibilità cioè di utilizzare lo stesso approccio matematico al variare della forma, variare che così, entro limiti dati e conosciuti, si rivela soltanto apparente dal punto di vista della teoria.

Marx affronta il problema in una sorta di analisi topologica sociale quando, nell'introduzione a Per la critica dell'economia politica parla delle categorie sociali invarianti, come il possesso, che rimane tale attraverso le varie forme di produzione, anche se trapassa in proprietà la quale, a sua volta, trapassa in proprietà capitalistica.

"Le categorie semplici", dice Marx, "sono espressione di rapporti in cui può essersi realizzato il concreto non sviluppato, senza aver ancora posto il rapporto o la relazione più complessa che è espressa mentalmente nella categoria più concreta; mentre il concreto più sviluppato conserva quella stessa categoria come un rapporto subordinato"[3].

Un mezzo universale di scambio è esistito prima che comparisse il denaro vero e proprio, lingotti di metallo, pelli di animale, animali in carne ed ossa (pecus, bestiame minuto, diventa pecunia), sale ecc. Ma il denaro propriamente detto percorre la sua parabola storica prendendo le forme di capitale mercantile, capitale industriale, profitto, salario, capitale azionario, capitale finanziario, infine segno di valore astratto registrato nelle memorie dei computer che registrano e compensano le transazioni senza che si muova denaro reale.

Una categoria semplice può esistere ben prima della sua forma sviluppata, ma essa è completamente rivelata soltanto quando si presenta come invariante all'interno di detta forma sviluppata, nel contesto sociale più complesso, più maturo. Per questo noi oggi diciamo che il marxismo si svela con maggiore potenza nella critica del capitalismo ultramaturo, proprio mentre il coro borghese e opportunista lo dà per morto.

La matematica scopre nella seconda metà del secolo scorso le proprietà invarianti delle figure geometriche sottoposte a determinate classi di trasformazioni (moti rigidi, compressioni, distensioni ecc.). Tali proprietà sono così strettamente connesse alla forma delle figure prese in esame che, sorprendentemente, esse persistono anche quando le figure sono assoggettate a deformazioni del tutto arbitrarie.

Senza saperlo, l'umanità aveva scoperto molti secoli prima, empiricamente, il concetto di invariante. I grandi maestri del Rinascimento che studiavano la prospettiva, cercando le leggi che governavano la trasposizione del mondo tridimensionale sulla tela bidimensionale senza perdere il senso della forma originaria, facevano un'operazione matematica con mezzi empirici. Quando Leonardo o Dürer studiarono la prospettiva cercando di proiettare l'immagine reale sulla tela, si accorsero subito che, se il centro di proiezione era il loro occhio, la struttura del dipinto, gli angoli e le misure delle cose si alteravano in proporzione della posizione relativa delle cose stesse tra loro e con l'occhio osservante. Nonostante queste variazioni, anche notevoli, non si perdeva la struttura geometrica dell'originale. Dovettero passare alcuni secoli perché si scoprisse che esistevano "proprietà geometriche invarianti rispetto alla proiezione o ai gruppi di trasformazione", ma soprattutto si dovette passare attraverso la rivoluzione borghese che, dando vita alla Scuola Politecnica di Parigi, gettò le basi per un salto scientifico.

Bordiga registra lucidamente questo percorso nella citata riunione di Milano sottolineando che la sovrastruttura ideologica e scientifica "non si forma dal quotidiano affluire di grani di sapere, ma appare nello squarcio di un violento scontro, e guida la classe che esprime, in una forma sostanzialmente monolitica e stabile (...) la successiva rivoluzione storica"[4].

D'altra parte, trasportando il concetto di "invarianza" nel campo sociale, oltre a demolire il dualismo implicito nella precedente separazione tra campi diversi, il marxismo introduce una dinamica che rifiuta la trasformazione del risultato acquisito in "rivelazione, mito, idealismo": l'invarianza intesa dinamicamente è la scienza di un mondo in movimento e, in ambito scientifico, ogni variazione deve poter essere descritta formalmente a partire dai dati conosciuti, altrimenti tutta la costruzione cade.

Il marxismo rimane perciò invariante anche se variano coerentemente "le grandezze in esso contenute" come affermato nella seconda definizione di dizionario citata. Detto in altri termini, l'invarianza non è garantita dalla sola conservazione della dottrina, che diventerebbe religione, ma dalla elaborazione del suo contenuto in un corpo teorico che si perfeziona al limite fino alla prossima rivoluzione. Ciò non significa che occorre correggere la teoria secondo i capricci della contingenza, operazione che stravolgerebbe la teoria stessa, ma che occorre conservare il suo contenuto in uno spostamento al gradino superiore.

Il concetto della necessità di conservazione dell'invariante e nello stesso tempo di elaborazione verso una migliore disposizione degli strumenti teorici, Bordiga lo esprime chiamando i militanti rivoluzionari ad un lavoro teorico che non è affatto di routine ideologica sulle bibbie marxiste, come amano ripetere gli avversari, ma vero lavoro pratico, che si basa su di una struttura organizzativa, sulla stampa, sul contatto con la classe operaia, su frequenti riunioni di lavoro che permettono l'osmosi fra centro e periferia e viceversa, sul mantenimento di una fede anticapitalistica riverberata soprattutto dalla stampa.

Per Bordiga non ha senso l'obiezione secondo cui il lavoro su testi "invarianti" si riduce ad un circolo vizioso di ripetizione. Nessun testo è perfetto, irrevocabile e immodificabile. Non si modifica il testo, naturalmente, ma i materiali in esso contenuti, come quelli contenuti in tutti i testi, materiali che "sono in continua elaborazione e destinati a pervenire ad una forma sempre migliore e più completa (...) È solo nello sviluppo in questa direzione del lavoro (...) che noi attendiamo il dilatarsi quantitativo delle nostre file e delle spontanee adesioni (...) che ne faranno un giorno una forza sociale più grande"[5].

Il concetto di invarianza come fin qui descritto spiega perfettamente la posizione di Bordiga, altrimenti incomprensibile, come succede alla maggior parte dei suoi frettolosi lettori. Non c'è affatto contraddizione fra l'affermata monoliticità della teoria e la sua elaborazione in forme più articolate. Non c'è contraddizione fra l'invito a ripetere e l'invito a lavorare per portare la teoria ad un livello superiore di compiutezza.

C'è una terza possibile definizione di "invariante". Ogni procedimento scientifico porta l'uomo, nel suo sforzo di comprendere il mondo che lo circonda, a non limitarsi ad osservarlo per ottenere i dati che gli servono al fine di controllarlo e prevederne il comportamento. Tra l'osservazione e la prevedibilità occorre introdurre il calcolo, qualsiasi tipo di calcolo. L'osservazione sulla realtà fisica offre soltanto un cumulo di dati, ma l'osservazione sui dati offre la possibilità di intravvedere delle strutture ordinate. Quando una struttura è individuata, è possibile sostituire una complicata sequenza di eventi con una formula abbreviata, il cui contenuto informativo sia identico o molto approssimato alla realtà.

Se la formula è ripetibile in tutte le occasioni sulla stessa classe di fenomeni e ci permette di prevedere gli eventi anche in condizioni nuove, abbiamo individuato una legge. Questo procedimento, che la scienza borghese riteneva applicabile solo a fenomeni "newtoniani" e non a fenomeni complessi quali la dinamica dei fluidi, l'economia e la dinamica sociale, da un paio di decenni viene invece applicato ai fenomeni sempre più complessi. Questo fatto è di importanza enorme nella dimostrazione che di fronte al marxismo la borghesia è costretta a capitolare.

Ecco una terza definizione che mettiamo direttamente in relazione con la già citata nota di Bordiga scritta mezzo secolo prima:

"La parola invariante descrive un processo comune a tutte le scienze matematiche e più in generale fisiche e naturali. In questa nozione è racchiusa a priori l'idea di matematizzare la realtà, ovvero di trasformare problemi qualitativi in problemi quantitativi e quindi costruire formalismi astratti e il calcolo su di essi"[6].

La nota di Bordiga agli Elementi dell'economia marxista del 1929 (vedi primo capitolo) serve per spiegare al lettore quanto sia importante indagare i fenomeni qualitativi in modo da trarne informazioni per un calcolo quantitativo, l'unico che ci permette di fare scienza. Tutta la società umana, a partire dall'economia, è riducibile a dati quantitativi e ciò ci permette sia di comprenderne la realtà, sia di prevederne il percorso, quindi di stabilire la transitorietà del modo di produzione attuale, capitalistico.

Il principio di induzione completa: n+1

"Henry Poincaré, ha potuto mostrare che anche in questa verità si nasconde una convenzione, ossia un arbitrio, alla fine. Già Leibnitz aveva cercato di dimostrare il teorema 2 + 2 = 4. Ma non era che una 'verificazione'. Tutte le nozioni di aritmetica elementare non sono dimostrabili che ammettendo per buono il 'principio di ricorrenza', cioè che se si possono fare date operazioni su n, si potranno fare su n + 1. Occorre inoltre avere definito questo famoso uno in modo che sia proprio quello al principio degli aggettivi numerali, e quando lo affibbio al numero n con quel segno più. Quando poi affibbio tutti quegli uni ad enti concreti, per dati sviluppi e calcoli, devo ritenere che siano tutti identici nelle condizioni reali di ambiente... forse è più facile definire la Divinità che l'unità, di cui ci serviamo mille e mille volte al giorno; ed è in fondo Pacelli che cammina sul sicuro; sul comodo".[7]

Poincaré doveva piacere non poco a Bordiga perché aveva espresso i suoi stessi concetti a proposito della logica. Aveva ad esempio criticato in modo molto acceso Russel il quale intendeva dimostrare che si può ridurre la matematica a logica. La logica, dice Poincaré, è scienza astratta e formale; può essere utile per sistematizzare la conoscenza a proposito della matematica, ma è assolutamente ininfluente sullo sviluppo della matematica come scienza. L'aritmetica e l'analisi sono scienze induttive e quindi rientrano nel "principio di ricorrenza", chiamato anche da Poincaré "principio di induzione completa".

Essendo il progresso della matematica induttivo, cioè basandosi sulle conoscenze del tutto nuove che esso stesso provoca nel suo corso, non può essere continuo, per ciò stesso non c'entra con la logica che presuppone sempre il sillogismo se - allora. Solo il modo di ragionare matematico ci permette di compiere il salto qualitativo dal finito all'infinito: una volta che il nostro cervello ha imparato a compiere una certa operazione e la può ripetere più volte con lo stesso risultato, esso è in grado di reiterarla all'infinito, sia materialmente che idealmente. Ma allora questo modo di ragionare si può chiamare assioma, mentre quello di Russel non è che un postulato. Gli assiomi sono dimostrativi, mentre i postulati sono semplici ipotesi. Per dimostrare la propria tesi, Russel interpreta i suoi postulati come assiomi e ciò è sbagliato.

Poincaré ritiene che la possibilità di concepire un concetto come quello di "classe di trasformazioni" sia una facoltà a priori del cervello, la manifestazione esteriore di un certo suo modo di funzionare. Per quanto ci sia un po' di linguaggio kantiano, in questo apriorismo si riconosce la presenza degli invarianti. Sappiamo che Poincaré era "filosoficamente" vicino a Felix Klein e sappiamo che Klein è il padre della teoria degli invarianti. Peano era con entrambi al Congresso di Genova dove si sviluppò la polemica contro Russel nel 1904, Bordiga aveva 15 anni e non si interessava ancora di politica.

Ma quando incominciò a studiare il problema dello sviluppo delle forme di produzione attraverso le "catastrofi" rivoluzionarie, doveva avere presente quel tipo di riflessioni. La sua battaglia "giovanile", che inizia e si conclude nel 1911-12, è già condotta sulla base di una solida teoria. Il quadro teorico della battaglia di sessant'anni non cambierà più:

"Per la descrizione del comunismo e del suo avvento non occorre a noi altro materiale di quello predisposto da Marx nel 1858, un secolo addietro, ossia la serie dei modi produttivi che parte dal primitivo comunismo tribale ed è già pervenuta a darci saggi storici maturamente sviluppati del modo moderno: mercato - capitale - salario. Non abbiamo razzi e missili truffaldini da aggiungere a quelle 'armi convenzionali' della lotta di classe, in dottrina già ben affilate in quel 1858. Da allora non diciamo che la storia si è fermata, ma che ha continuato a discendere nel pattume della fogna borghese, e da allora come partito, e si adonti chi vuole, sappiamo tutto".[8]

Così inizia un passo del 1958 in cui ci si riferisce alla serie di Marx in cui compaiono gli invarianti storici entro i modi successivi di produzione, possesso, proprietà, proprietà capitalistica ecc.

Il concetto di Poincaré sulla convenzionalità delle notazioni simboliche viene utilizzato per una serie finita e non per una ricorrenza infinita; con questo si dimostra che effettivamente l'opportunista trova più fecondo definire la Divinità che non l'unità, dato che introduce per comodo suo delle mezze unità di transizione che non c'entrano con la serie.

"Questo nostro centrale teorema contiene lo sbugiardamento di tutte le menzogne revisioniste che circolano. È facile enunciarlo, sempre a fine non di esaurire lo sterminato tema, ma di chiarificarne e rinvigorirne la duramente raggiunta presentazione.

Lo diremo, a rabbia dei chiaccheroni 'a soggetto', in modo schematico. Se le forme o modi sociali col capitalismo sono state n, in tutto esse sono n + 1. La nostra rivoluzione non è una delle tante, ma è quella di domani; la nostra forma è la prossima forma".[9]

La serie dei modi di produzione non è progressiva all'infinito, 1-2-3-4 ecc. che sarebbe come dire n+1, n+2, n+3, n+4 ecc. Tale serie è tripartita in grandissime epoche dell'umanità che sono: comunismo primitivo; epoca delle società proprietarie; comunismo sviluppato.

Applicando gli invarianti alle forme di produzione troviamo che le tre epoche rappresentano degli "insiemi" che sono sovrapponibili solo a coppie: il comunismo primitivo ha in comune con il comunismo sviluppato solo il fatto di non conoscere la proprietà, ma il comunismo sviluppato conosce la produzione di surplus che invece è conosciuta solo dall'epoca intermedia. D'altra parte sembrerebbe che le due prime epoche non abbiano nulla in comune, mentre sono abbinate dialetticamente da Marx per il fatto di rappresentare, insieme, l'intera preistoria umana ("l'avvento del comunismo rappresenta la fine della preistoria umana").

La formulazione che interessa Bordiga è quindi quella che stacca la rivoluzione comunista dalle forme precedenti. Per questo l'insieme delle forme proprietarie e sfruttatrici con il comunismo primitivo, la preistoria umana, è rappresentato unitariamente dal simbolo "n". Per questo il segno "+" non può che rappresentare la fine della serie (il secondo assioma di Peano afferma che il segno "+" messo dopo un numero produce un numero). Ma nel corso di questo libro abbiamo visto che Marx comprende nel capitalismo sviluppato tutti gli invarianti dei modi di produzione precedenti, quindi n è il modo di produzione che determina tutti gli altri, li contiene.

"Il comunismo diverrebbe in teoria la forma n + 2, se comparisse una forma di più che sia già post-capitalismo e non sia ancora comunismo; comunismo con tutti quei precisi caratteri che abbiamo sviscerati partendo dai caratteri differenziali tra il capitalismo che intorno ci appesta e le forme a cui esso è seguito. Se così fosse, non sarebbe giunto un secolo e più fa il momento storico per fondare il sistema invariante della rivoluzione, come dottrina, come partito, come combattimento".[10]

Dire n + 2 significa già, nella nostra notazione simbolica e in realtà, essere anticomunisti. Chiunque infatti sostenga che esiste la possibilità di un trapasso graduale da una forma di produzione all'altra attraverso aggiustamenti delle forme precedenti non è comunista ed è automaticamente schierato contro i grandi avvenimenti storici che preparano il salto qualitativo da un tipo di società all'altro.

Se quindi neghiamo la possibilità di una forma n + 1 non comunista è perché neghiamo nel tempo stesso l'aberrazione staliniana che sia socialismo la sopravvivenza di capitale, del salario e lo scambio secondo valore. La Russia staliniana era a tutti gli effetti dentro n e non se ne toglieva solo per il nome che Baffone e tutti i suoi seguaci le davano.

E di fronte al nostro schema non se la cavano meglio i trotzkisti che di fronte al fenomeno russo abbandonano n ma chiamano n + 1 l'ibrido del tutto fantastico dello "Stato operaio degenerato", quella dominazione della burocrazia che non sarebbe più capitalismo e non è ancora socialismo. Peano aveva ragione e Bordiga lo dimostra: con lo schema si sbugiardano i pasticcioni contaballe, perché al di là delle belle parole i grandi nemici staliniani e trotzkisti devono per forza giungere alla formula comune n + 2 per il comunismo. Essendo fallita la rivoluzione in Occidente, la rivoluzione russa ha dovuto abortire i compiti di doppia rivoluzione e limitarsi ad essere una rivoluzione antifeudale n -1.

Facciamo un passo necessario. Se chiamiamo N (maiuscolo) l'insieme delle forme successive di produzione fino al capitalismo sviluppato, possiamo dire che la rivoluzione russa è stata una delle n-sime (minuscolo) formazioni sociali determinate da N.

Oggi è facile constatarlo guardando al capitalismo esplosivo, crudele e arraffone della Russia contemporanea, vero sottoprodotto di N, ma i meno giovani ricordano perfettamente cosa significava per uno staliniano anni '50 il paradiso sovietico. Mancando la scienza che sostiene la fede rivoluzionaria, la fede soltanto diventa allucinazione e la professione di "comunismo" assume la stessa natura delle psicosi collettive attorno alle apparizioni della Madonna. Eppure il nostro schema non teme smentite.

Applichiamo il principio di ricorrenza:

N sia il modo di produzione che determina n formazioni sociali.

N è vero per n = 1 (poniamo l'Inghilterra).

Se è vero per l'Inghilterra (cioè per 1), è vero per 2 (poniamo la Francia).

Quindi è vero per 2

Se è vero per 2, è vero anche per 3.

Quindi è vero per 3, e così di seguito finché N coinvolge tutte le forme comunitarie in tutte le aree del mondo e dà luogo a tutte le n forme sociali specifiche.

La similitudine esiste solo tra N e N + 1; entrambe sono per la prima volta nella storia degli invarianti alla scala universale. Il passaggio da N a N + 1 è irreversibile: non vi potrà essere ritorno né a N né a N - 1. Con il comunismo, la preistoria dell'umanità è davvero lasciata alle spalle per sempre.[11]

La tragedia dello stalinismo coinvolse anche le file di quei rivoluzionari che stalinisti non erano ma non riuscivano a capire l'importanza dei trapassi storici da un modo di produzione all'altro e guardavano alle rivoluzioni nazionali sottovalutandone l'importanza dato che, dicevano, nella nostra epoca solo la rivoluzione proletaria deve far convergere tutta la nostra attenzione. Lo stalinismo commise la follia di legare le rivoluzioni nazionali dei popoli non bianchi agli interessi imperialistici dello Stato russo e, nella competizione con l'imperialismo americano, la lotta per la libertà, per la democrazia e contro le basi americane divennero lo scopo principale di tutti i partiti "comunisti" del mondo. Bordiga chiamò indifferentismo l'atteggiamento di chi sottovalutava per reazione la lotta "democratica" dei popoli coloniali o ex coloniali.

"La stessa follia si ravvisa nel negare carattere di trapasso rivoluzionario alla rivoluzione nazional-liberale dei popoli di colore, per condannarli da un tribunale di fantasia alla immobilità e passività fino a che non possano spiccare lo stalinistico salto da n - 1 ad n + 1 improvvisando dal nulla la lotta di classe tra imprenditori capitalisti e proletari, ovvero facendosi iniettare dall'esterno una volontarista attuazione di socialismo, a cui non si può credere senza passare nel gregge di Stalin.

È indiscutibile che fin dall'apparire del modo storico di produzione borghese in vaste parti del mondo, essendo una delle caratteristiche della forma capitalista il passaggio dall'obbiettivo interno, mercato nazionale (che vuol dire indipendenza nazionale, Stato nazionale borghese), all'obbiettivo esterno del mercato mondiale, termine essenziale in Marx, il moto generale si accelera grandemente e gli scarti di tempo nei passaggi tra forme sociali in diverse zone geografiche divengono minori. La rivoluzione borghese del 1848 in Europa, che ebbe alleata la classe operaia rimbalzò in pochi mesi dall'una all'altra delle grandi capitali, e questo è esempio classico del tracciato marxista. Da allora la borghesizzazione e industrializzazione del mondo procede a ritmo invincibile. Quindi quella che abbiamo sempre chiamata doppia rivoluzione, e che ora diremo rapido passaggio da n - 1 ad n, e poi da n ad n + 1, si presenta come un'eventualità storica fortemente probabile, come si era presentata per la Russia. Ma la sua condizione era internazionale, ossia la rivoluzione politica e la trasformazione sociale nei paesi di capitalismo già maturo, come passaggio da capitalismo a socialismo.

La dottrina della sinistra ha provato che la rivoluzione russa, mancate e tradite le rivoluzioni occidentali (da n a n + 1) si è dovuta ridurre ad una pura rivoluzione capitalista (da n - 1 a n). Ma indubbiamente gli effetti del fallimento - più che tradimento di persone - stalinistico sono lì. Non essendo storicamente da attendersi rivoluzioni comuniste vere in Occidente e per ora nemmeno in Russia, in quanto non si vedono partiti organizzati per la presa del potere e sul giusto programma rivoluzionario, gli altri paesi ancora pre-capitalistici non ci possono dare rivoluzioni doppie, come si poteva sperare per la Russia, nel periodo fecondo per l'Europa del primo dopoguerra".[12]

Il rovesciamento della prassi

S'è creduto di danzare sulle spoglie del determinismo di Laplace. Ma il caso è un concetto del tutto negativo, vuoto, e dunque spoglio di interesse scientifico. Il determinismo, invece, è un oggetto di affascinante ricchezza, per quanti sappiano esaminarlo (René Thom, Basta con il caso, taccia il rumore).

Il lettore attento che, scorrendo il testo di Bordiga Teoria e azione nella dottrina marxista del 1951, giunga alla sintetica spiegazione dello schema sulla successione delle forme di produzione, non mancherà di stupirsi alla lettura di quelle poche righe. Due schemi sono messi a confronto: quello che rappresenta la concezione gradualistica delle variazioni storiche, a forma sinusoidale continua, e quello della concezione rivoluzionaria che invece rappresenta i rapporti di produzione come fasi spezzate (vedi figura più avanti). La differenza fra i due schemi viene così spiegata:

"La prima curva o curva degli opportunisti (...) è una curva continua che in tutti i punti 'ammette una tangente', ossia praticamente procede per variazioni impercettibili di intensità e di direzione. La seconda curva, con cui si è voluta dare una immagine semplificatrice della tanto deprecata 'teoria delle catastrofi', presenta ad ogni epoca delle punte che in geometria si chiamano 'cuspidi' o 'punti singolari'. In tali punti la continuità geometrica, e dunque la gradualità storica, sparisce, la curva 'non ha tangente' o, anche, 'ammette tutte le tangenti' - come nella settimana che Lenin non volle lasciar passare".

Il commento di questo passo richiederebbe ben più spazio di quanto qui ci sia concesso, ma ci accontenteremo dell'essenziale. "Teoria delle catastrofi" oggi evoca unicamente il lavoro di René Thom che va sotto quel nome e che in realtà l'autore ha chiamato, con espressione meno giornalistica e assai significativa, Stabilità strutturale e morfogenesi. Nel 1951 non potevano essere conosciuti neanche gli stadi iniziali di tale lavoro e tantomeno il nome dato alla teoria, che è successivo alla sua pubblicazione (1972; in italiano sarà pubblicato da Einaudi solo nel 1980).

Bordiga si riferisce quindi alla "tanto deprecata" teoria del catastrofismo rivoluzionario, che risale a Marx ed Engels, ma che è mutuata da Hegel, il quale studiò dal punto di vista filosofico il passaggio repentino delle forme o degli stati in fisica. Il mutamento continuo della temperatura dell'acqua è un mutamento quantitativo che non cambia la natura dell'acqua, perché essa conserva le sue proprietà non misurabili, cioè le sue qualità. Ma l'acqua ad un certo punto diventa ghiaccio o vapore. Se ci si attiene all'apparenza del fenomeno, il mutamento qualitativo, che è un salto, una rottura di continuità, non sembra avere relazione con il mutamento quantitativo. Invece, conclude Hegel, la relazione c'è (oggi diremmo che gli atomi sono sempre gli stessi). Marx utilizza l'argomento per dimostrare il salto qualitativo dal denaro, esistente da millenni, al valore-Capitale, fenomeno recente, e cita direttamente Hegel. Engels riprende il discorso nell' Antidühring (Il Capitale, libro I, cap. IX. Antidühring, Prima sezione cap. XXII).

Il lettore stupito si è già tranquillizzato dopo essersi dato questa prima spiegazione, quando subito dopo l'inciso deve ricredersi: c'è effettivamente la descrizione, ridotta all'osso, della teoria delle catastrofi di Thom. Per quanto la coincidenza sembri sensazionale, essa è invece del tutto "normale": Bordiga non è un "vate" che anticipa di oltre vent'anni la scoperta, ma un utilizzatore di scoperte borghesi a fine rivoluzionario. La definizione coincide perché in ogni caso la scelta delle parole non poteva essere vasta più di tanto. Ma coincide anche il succo della teoria perché essa scaturisce da scoperte che "erano nell'aria" e che Thom riuscì a formalizzare. Bordiga doveva conoscere gli antecedenti della teoria delle catastrofi perché risalgono ai primi trent'anni del secolo e, tra gli altri, troviamo all'origine del percorso anche Poincaré, ispiratore di Thom.

La moderna teoria delle catastrofi è per noi interessante perché mette in discussione una volta di più il dualismo tra quantitativo e qualitativo e in fondo si colloca positivamente nel grande filone della nostra teoria della conoscenza. Inoltre è perfettamente inserita nei "sistemi" deterministici, quindi è uno strumento in più per combattere le teorie del dubbio e dell'indeterminato. Infine, è in grado di descrivere una classe di fenomeni molto ampia: praticamente qualunque transizione discontinua che si verifichi in un sistema che sia composto da due o più stati stabili. In senso dinamico essa spiega un sistema che possa seguire più di un percorso stabile di trasformazione. Un esempio un po' rozzo ma efficace può essere quello di una biglia che si muove su un piano (stato stabile) e finisce per cadere (catastrofe) su un altro. La catastrofe propriamente detta è quindi il passaggio repentino da uno stato all'altro o da un percorso all'altro (anche un asse che si spezza sotto un peso crescente è una catastrofe). Si incomincia a capire che la questione ha molta attinenza con la struttura dei cambiamenti sociali: da una situazione stabile, cambiamenti continui e impercettibili portano alla rottura discontinua, al salto rivoluzionario in un'altra forma sociale.

I sistemi viventi, che sono i più restii a lasciarsi formalizzare e sono visibilmente non-statici, si possono anche definire in "equilibrio dinamico", frase che a prima vista sembra una contraddizione. In effetti, sia gli organismi individuali che la società di individui, assorbono e trasformano continuamente energia. Nessuno stato all'interno di tali sistemi può essere stabile, ma l'insieme degli stati resiste straordinariamente alle perturbazioni perché ogni stato interagisce con l'altro annullando gli effetti a cascata di eventi singolari.

Figura 1

Il diagramma delle successive forme di produzione (cuspidi, vedi figura 1) ideato da Bordiga offre la visione d'insieme delle successive transizioni di stato, ma la visione "fine" del processo non è spiegata. Tale spiegazione dettagliata compare nel diagramma del "rovesciamento della prassi" (vedi più avanti), anche qui posto in relazione ad altri diagrammi che schematizzano le varie concezioni opportunistiche. Per evidenziare quanto sia aderente lo schema di Bordiga alle moderne formalizzazioni della complessità - teoria delle catastrofi, matematica del caos, frattali, biforcazioni ecc. - metteremo a confronto due procedimenti in antitesi, il primo di Ilya Prigogine (indeterminista), il secondo di René Thom (determinista).

Figura 2

Nell'esempio di Prigogine alla figura 2 (a), per un dato valore (l') del parametro di controllo l, il sistema può assumere, alla biforcazione B, tre diversi stati stazionari: C, E, D. Due di questi sono stabili, mentre uno è instabile. Al variare del parametro di controllo l possiamo seguire a piacere il percorso A,B,C sulla figura. Al contrario, al variare di X, fermo rimanendo il parametro di controllo l, si giunge al punto D. In ogni caso, lo stato che si raggiunge dipende dalla precedente storia del sistema. Questo tipo di determinismo è stato provato sia in colture biologiche, sia in concentrazioni chimiche. Prigogine osserva:

"Finora la storia era stata adoperata, normalmente, per l'interpretazione dei fenomeni biologici o sociali. Che essa possa giocare lo stesso importante ruolo in elementari processi chimici, è piuttosto sorprendente" (Ilya Prigogine e Isabelle Stengers, La nuova alleanza, Cap. quinto, 6: "Biforcazioni e rotture di simmetria", Einaudi 1981).

Ma nella figura 2 (b) Prigogine osserva che ora il diagramma di biforcazione, a differenza del precedente, presenta due soluzioni simmetriche e stabili

"Dove andrà il sistema quando arriva al punto di biforcazione?" si chiede. "C'è qui una scelta fra due possibilità (...) come farà il sistema a scegliere fra destra e sinistra? Siamo di fronte ad un elemento irriducibilmente casuale".

Ogni sistema, aggiunge l'autore, posto di fronte a biforcazioni multiple (a cascata) in cui è indecidibile la "scelta" (e già avremmo da dire sul termine) fra diversi possibili futuri, rappresenta una transizione al caos. Dalla commistione fra caos e necessità, in presenza di piccole perturbazioni del sistema, può nascere un nuovo ordine. Questa è la stessa conclusione a cui giunge Jacques Monod nel suo celebre saggio Il caso e la necessità (Arnoldo Mondadori, 1970. Su questo saggio è disponibile una nostra critica: "Comment Mr. Monod terrasse la dialectique", Programme communiste n. 58, aprile 1973).

Nella teoria di René Thom, il punto di partenza per la rappresentazione della "catastrofe" più semplice, assomiglia molto ad un diagramma di biforcazione in cui uno degli assi è il solito fattore di controllo e l'altro è il comportamento generale del sistema verso un "massimo" o un "minimo".

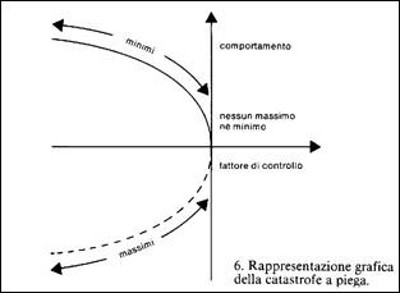Figura 3

Il comportamento qualitativo di tale sistema è molto semplice. Per certi valori del fattore di controllo esistono sia massimi che minimi e il sistema è stabile con una attrazione verso i minimi. Ad un valore critico del fattore di controllo il sistema assume un equilibrio incerto, mentre al di là del valore critico diventa completamente instabile. Questo modello contiene troppo poca informazione per essere esplicativo di fatti reali, ma serve per capire il meccanismo della teoria: tutto dipende dal fattore di controllo. Thom aggiunse che quello degli indeterministi è un trucco volgare, perché nessun sistema presenta tratti isolati corrispondenti a un diagramma di biforcazione perfettamente simmetrico (figura 3). Ogni "storia" dei singoli percorsi possibili è in relazione con l'universo delle storie adiacenti; e il fatto stesso che l'indecidibilità venga risolta con una ricerca statistica dei risultati dimostra che vi è una regolarità statistica, quindi un substrato deterministico. Nella dinamica dei fatti sociali la "teoria delle catastrofi" come la intendeva Bordiga ha più fattori di controllo (lo vedremo fra poco), ma il semplice diagramma di biforcazione simme0siderazioni in rapporto alla teoria marxista del partito.

Thom, criticando Prigogine, non escluse affatto che la dinamica dei sistemi complessi contenesse dei punti singolari che conducono alle biforcazioni; o, se la biforcazione è impercorribile, alla "catastrofe". Solo che

"Il gioco intellettuale dei teorici del caos dall'ordine e dell'ordine dal caos, cioè del caso e della necessità, è consistito nel cancellare mentalmente l'ambiente dinamico globale - sempre deducibile da un esame sufficientemente completo della base su cui il sistema si sviluppa - a vantaggio della piccola perturbazione scatenante cui segue il crollo della stabilità imperfetta del sistema verso un equilibrio di energia inferiore. L'artificio sta nel far credere che l'evoluzione successiva, dagli effetti spettacolari, sia effettivamente creata dalla 'fluttuazione' scatenante. (...) Un esame sufficientemente completo della base su cui il sistema si sviluppa permette di prevedere a priori i possibili esiti della biforcazione, che preesiste alla fluttuazione scatenante. Spetta a quest'ultima il ruolo di innescare il processo ed eventualmente di determinare, con una scelta apparentemente arbitraria, fra tutti gli esiti possibili l'ulteriore evoluzione. Ma certo non la crea".

Ci scusiamo con l'autore per aver modificato un pochino il linguaggio eccessivamente tecnico a favore di chi legge. Nella dinamica rivoluzionaria formalizzata da Bordiga con lo schema del rovesciamento della prassi, abbiamo: 1) una analisi della base su cui il sistema si sviluppa in cui si individuano 2) quattro "parametri di controllo" la cui dinamica porta 3) a una biforcazione indecidibile (continuazione del capitalismo o rovina di tutte le classi) per cui si presentano tutte le tangenti o nessuna tangente sulla cuspide (la settimana che Lenin non volle lasciar passare) e quindi 4) si rovescia la prassi perché il partito, prodotto della storia, ne diventa fattore soggettivo, rappresentando la "volontà".

Figura 4

Nella teoria delle catastrofi di Bordiga i quattro parametri di controllo (vedi figura 4) sono rappresentati in uno schema a due dimensioni, mentre nella teoria di Thom sarebbero rappresentati in quello che viene chiamato "grafico di catastrofe a farfalla" che si svolge in uno spazio a più dimensioni. Lo schema di Bordiga dimostra che, in prossimità della biforcazione, nella polemica tra Prigogine e Thom, ebbe ragione Thom: l'ambiente, l'universo delle determinazioni da cui nessun atomo sociale può sottrarsi, essendo polarizzato dalla convergenza di interessi che contrappongono non più individui ma blocchi interi della società, classi, porta lo strumento partito a scegliere. E qui il termine non ha più quel senso di "libero arbitrio" che Prigogine assegna ai fenomeni dinamici. Non sappiamo se Thom fosse anticomunista come tutti i suoi colleghi dediti alla scienza pagata dalle università borghesi, ma il cervello sociale ha il sopravvento su quello individuale del ricercatore, e questo è un duraturo insegnamento proprio di Bordiga. Del resto proprio Thom registrò il fenomeno quasi con le stesse parole di Bordiga:

"Molte acquisizioni della scienza sono indubbiamente vere, ma il loro interesse è debole, quasi nullo. Il vero problema è rintracciare la fonte dell'interesse. In alcuni casi si tratta di una fonte sociologica locale: un risultato è interessante semplicemente perché il finanziatore della ricerca ha sottoposto allo scienziato un problema che questi ha tutto l'interesse di risolvere, se non altro per fare carriera".

Ma vi sono alcuni casi in cui la ricerca rientra nel bisogno di conoscenza globale, che è il vero scopo, quello che serve per "decifrare il mondo, renderlo intelligibile"; allora l'interesse non è più venale, perché "svelare una struttura soggiacente che renda i fenomeni intelligibili" significa adottare quel metodo dell'astrazione che, dedotto da Hegel, Marx ha potentemente mutuato e rovesciato, e che Bordiga rivendica in ogni sua riunione, in ogni suo scritto sui problemi della conoscenza. Sostituire un visibile complesso con un invisibile semplice (astratto) non è problema di interpretazione della realtà, ma di rivelazione della realtà.

L'impresa di rivelare la struttura soggiacente della società capitalistica, che contiene in sé tutti gli invarianti delle precedenti società, sembrerebbe un compito impossibile al pari dell'impresa di ordinare in qualche schema l'infinità dei movimenti e dei cambiamenti propri dell'intero mondo che ci circonda. Bordiga ha letto Leibnitz e la sua "legge di continuità" (1687) che prevede un certo ordine nelle domande per avere un ordine nelle risposte; ha studiato certamente i risultati delle ricerche di Poincaré e seguito il dibattito sulla stabilità del sistema solare (P. es. Duhem, 1914), da cui si ricava che il problema delle perturbazioni che portano alle "catastrofi" in fondo è il problema della validità del determinismo.

La fatidica domanda cui rispondere è: se un sistema dinamico subisce perturbazioni continue e tende matematicamente ad ampliarle fino a che piccole variazioni iniziali producono grandi cambiamenti finali, come mai, praticamente, la maggior parte delle forme (compreso il capitalismo) rivela una robustezza insospettata rispetto alle piccole perturbazioni? Per rispondere secondo il linguaggio "catastrofista" diremo: esiste una stabilità strutturale insensibile a singoli elementi critici, ma nello stesso tempo essa è messa in discussione da perturbazioni che, in fasi del tutto determinate, possono portare a rotture discontinue. La comprensione dei fenomeni è resa possibile dalla loro riduzione tramite processi di astrazione.

La teoria delle catastrofi ha provocato adesioni e critiche, ma una cosa ha dimostrato: l'impresa, un tempo disperata, di dare spiegazione al numero infinito di forme e comportamenti si dimostra fattibile dato che, sottoponendo tali forme e comportamenti ad alcuni vincoli, alla fine se ne trova un numero finito di tipi, secondo Thom e i suoi allievi soltanto sette.

Nello schema di Bordiga è anche spiegata la genesi di teorie borghesi che avanzano parallelamente al marxismo ed in ritardo rispetto ad esso. Le determinazioni che salgono dalle spinte fisiologiche elementari dell'individuo verso l'attività cosciente dell'organizzazione, si invertono: l'attività cosciente dell'organizzazione determina il comportamento delle classi e l'azione degli individui, mentre l'influenza rivoluzionaria neutralizza l'influenza conservatrice e consente il salto sociale. Prima che succeda questo salto, è inevitabile che i bisogni reali della produzione e della ricerca producano molte di queste capitolazioni ideologiche borghesi di fronte al marxismo.

Poiché ogni schema di catastrofe (dei sette tipi possibili) deve rispondere al "vincolo di Leibniz" sopra ricordato, la ricerca intorno alla discontinuità nei sistemi dinamici non può assumere la discontinuità stessa come dato della dinamica. I ricercatori che hanno lavorato sulla ricchezza potenziale della teoria di Thom hanno osservato che il concetto di "spiegazione" implicito nella teoria è rilevante anche sotto il profilo della tecnica matematica perché la pone nel grande filone classico della ricerca sul "continuo". Se questa interpretazione è corretta, e se Bordiga fosse vissuto abbastanza per venirne a conoscenza, tutto ciò gli sarebbe piaciuto assai. Scrive infatti nel 1956 a proposito della teoria della relatività (sottolineatura nel testo):

"Sostituito il tempo locale al tempo universale si può riscrivere la meccanica con formule nuove, ma sugli stessi principii di Galileo, di Newton, di d'Alembert, con le stesse equazioni canoniche... [Einstein] lascia ferma l'ipotesi di Cartesio e di Leibniz, ossia tutto misura con grandezze variabili gradualmente, dunque continue, applicando quindi il calcolo infinitesimale e i sistemi di coordinate [anche se] chiede tuttavia alle matematiche nuovi apparati" (Relatività e determinismo cit.).

Questa rivendicazione di una "scienza del continuo" è importante perché contribuisce ad avvicinare la scienza alla concezione unitaria dell'universo che è propria del marxismo. Einstein, aggiunge Bordiga, scrive "alla fine, la identità monistica e materialistica tra materia e pensiero". Come farebbe chiunque si trovasse a marciare sulla nostra stessa strada.

La concezione teorica "catastrofica" marxista espressa dallo schema del rovesciamento della prassi disegnato da Bordiga unisce in un rapporto dialettico il "substrato", cioè l'ambiente economico materiale che è l'arena delle relazioni umane, con gli effetti dell'ideologia e del "pensiero". L'azione del partito politico, che è sovrastruttura, diventa, al punto di catastrofe, forza materiale che provoca un cambiamento qualitativo di "stato".

"Il rapporto dialettico sta nel fatto che in tanto il partito rivoluzionario è un fattore cosciente e volontario degli eventi, in quanto è anche un risultato di essi e del conflitto che essi contengono fra antiche forme di produzione e nuove forze produttive. Tale funzione teorica ed attiva del partito cadrebbe però se si troncassero i suoi legami materiali con l'apporto dell'ambiente sociale, della primordiale, materiale e fisica lotta di classe" (Teoria e azione nella dottrina marxista cit.).

Alla luce di queste citazioni risulta più chiara una celebre quanto perentoria affermazione di Bordiga: le rivoluzioni e i partiti non si fanno, si dirigono (in "Partito e azione di classe", Rassegna comunista, 1921).

Un divulgatore scientifico che ha redatto un saggio sulla teoria delle catastrofi, pur non badando al rapporto dialettico fra il partito e l'ambiente che lo rende "prodotto e fattore di storia", è colpito dall'atteggiamento di Lenin nell'Ottobre, quando si presentò "la settimana da non lasciar passare". Tale autore registra a suo modo, un po' ingenuamente, la forza sovvertitrice del rovesciamento della prassi operato dal partito bolscevico:

"Durante gli eventi che condussero alla rivoluzione russa, si dice che Lenin fosse molto attento alla tempestività delle mosse dei bolscevichi per giungere al potere. Nelle circostanze adatte, disse, basterà una piccola 'spinta' per provocare una transizione che in un altro momento richiederebbe uno sforzo molto maggiore" (A. Woodstock e M. Davis, La teoria delle catastrofi, Garzanti 1982).

Eravamo partiti da una considerazione di Bordiga sullo stesso fatto: è interessante ritrovarla in un libro sulla teoria matematica delle catastrofi.

Note

[1] Dizionario Zingarelli.

[2] Dizionario Italiano Ragionato.

[3] Marx, Per la critica dell'economia politica, Editori riuniti, Roma 1968.

[4] Riunione di Milano del 7 sett. 1950, in Per l'organica sistemazione dei principii comunisti, cit.

[5] Tesi di Napoli, raccolte nel volume In difesa della continuità del programma comunista cit.

[6] Enciclopedia Einaudi, voce Invariante.

[7] Chiesa e fede, individuo e ragione, classe e teoria, 1950. Nel testo dallo stesso titolo ed. Quad. Int.

[8] La dottrina dei modi di produzione valida per tutte le razze umane, in "Il programma comunista", n. 3 del 1958. Ora in Ed. Quad. Int., stesso titolo.

[9] Ibid.

[10] Ibid.

[11] Dobbiamo questo sviluppo dello schema ai compagni di Berlino.

[12] La dottrina ecc., cit.

La passione e l'algebra
Amadeo Bordiga e la scienza della rivoluzione

Quaderni di n+1.

Scritto per i giovani lettori che non conoscono la storia della Sinistra, cancellata dalla memoria per opera congiunta dello stalinismo e della storiografia borghese.

Indice del volume

La passione e l'algebra