Capitolo III. Teoria della rendita
Scopo fondamentale di questo capitolo è la formulazione matematica delle leggi che regolano il processo di valorizzazione nelle sfere di produzione soggette al meccanismo della rendita. Per prima cosa prenderemo in esame le basi materiali su cui si fondano la rendita assoluta e differenziale nell'ambito della società capitalistica. Successivamente, verrà studiato il meccanismo di progressiva formazione della rendita differenziale nel corso del processo di accumulazione. I risultati di questa analisi costituiranno il punto di partenza per lo studio dei cicli di secondo e terzo ordine, che verrà portato avanti nel capitolo successivo.
3.1 - Rendita assoluta
Le teoria dell'equilibrio del meccanismo di riproduzione, sviluppata nel paragrafo 1.3, si fonda sull'assunto che il plusvalore venga accumulato nella stessa sfera in cui è stato prodotto (eq. 1.23). In altri termini, si suppone che in condizioni di equilibrio non avvengano trasferimenti di capitale da una sfera produttiva all'altra. Anche a prescindere dai meccanismi del credito, questa ipotesi appare plausibile solo nel caso in cui la redditività del capitale, ovvero il saggio del profitto, si mantenga costante passando da un nodo all'altro del sistema riproduttivo. In alternativa, l'equilibrio potrebbe essere mantenuto solo grazie a qualche meccanismo che ostacola la migrazione dei capitali. In effetti, nulla vieta che parte del plusvalore prodotto in una sfera possa essere trasformato in capitale addizionale in una sfera produttiva diversa, se le condizioni generali del mercato lo richiedono e non esistono vincoli al trasferimento di capitali da un ramo d'industria all'altro.
Il saggio del profitto τi relativo ad una singola sfera produttiva dipende, come abbiamo visto nel capitolo I, dai parametri Si ed Ωi associati a quel nodo del meccanismo di riproduzione. Questa grandezza, in quanto rappresenta il rapporto tra la massa di plusvalore prodotta (P) ed il costo dei fattori produttivi (C + V), definisce il "grado di redditività" del capitale impiegato in una sfera produttiva. Per gran parte dei rami d'industria la giornata lavorativa ed il salario hanno approssimativamente la stessa grandezza, ed il lavoro umano si presenta come lavoro semplice, per cui il saggio del plusvalore è un parametro globale che dipende essenzialmente dal grado di sviluppo delle forze produttive. Chiameremo questa grandezza saggio generale del plusvalore. In questo caso il saggio del profitto varia da una sfera all'altra solo a causa della diversa composizione organica dei capitali impiegati. Esso sarà tanto maggiore quanto minore risulta essere il rapporto tra parte costante e parte variabile del capitale. Tuttavia, in queste condizioni l'equilibrio non può essere mantenuto, in quanto la frazione del plusvalore complessivo della società destinata a trasformarsi in capitale addizionale verrà ripartita tra le diverse sfere produttive in base al criterio della migliore redditività, dunque in misura maggiore laddove il saggio del profitto risulta essere più elevato. Ora, un afflusso eccessivo di capitali in una sfera caratterizzata da un elevato saggio del profitto genera inevitabilmente un inasprimento della concorrenza, che a sua volta determina, attraverso la diminuzione dei prezzi, una progressiva diminuzione del saggio del profitto. Viceversa, un eventuale svuotamento relativo di capitali in una sfera produttiva a basso saggio del profitto determina un difetto di offerta per quel tipo di merci ed un conseguente aumento dei prezzi. Inevitabilmente ciò si traduce in un aumento del saggio di profitto di questa sfera. In questo modo il meccanismo di riproduzione raggiunge uno stato di equilibrio nell'ambito del quale τi = τ per ogni ramo d'industria libero da vincoli. La grandezza τ che si viene a formare viene detta saggio medio del profitto e determina una ripartizione uniforme del plusvalore complessivo della società tra le diverse sfere di produzione, indipendentemente dalle proporzioni in cui è stato prodotto e incorporato nelle loro produzioni. Esso viene in effetti suddiviso in proporzione alla grandezza del capitale anticipato in ogni singola sfera, in modo che i capitalisti che in essa operano ottengono un profitto medio dato da:
 (3.1)
(3.1)Questo risultato, il quale può essere ottenuto, ripetiamo, in regime di libera concorrenza e a condizione che i capitali possano liberamente migrare da una sfera all'altra, richiede però che le merci vengano vendute a prezzi che in generale non rispecchieranno il contenuto di valore dei singoli prodotti. Questi prezzi vengono detti prezzi di produzione e forniscono, oltre al capitale anticipato, un profitto medio uguale per capitali di uguale grandezza, indipendentemente dalla loro composizione organica. Inoltre, in base a quanto detto precedentemente, si deduce che il prezzo di produzione di una merce sarà sempre superiore al valore di mercato quando la composizione organica del capitale operante in questa sfera supera la composizione organica media. Viceversa, esso sarà sempre inferiore al valore quando la composizione organica è inferiore alla composizione media.
Da quanto detto appare chiaro che l'equilibrio del meccanismo di riproduzione costituisce una condizione limite. Questa condizione viene continuamente raggiunta attraverso il meccanismo di livellamento dei valori ai prezzi di produzione e mediante la formazione di un saggio medio del profitto, per essere poi nuovamente spezzata dai mutamenti tecnici che periodicamente sconvolgono la struttura del processo produttivo nella maggior parte delle sfere del sistema di riproduzione.
Queste considerazioni ci portano a concludere che, in condizioni di equilibrio di mercato, la coincidenza tra prezzo e valore può verificarsi solo in tre casi: 1) quando la composizione organica di una sfera produttiva coincide con la composizione organica media, in altri termini quando si verifica la condizione Ωi = Ω; 2) nel caso del capitale complessivo della società e 3) quando esiste un vincolo all'introduzione di capitali in una particolare sfera produttiva. Mentre le prime due situazioni sono abbastanza ovvie, in quanto il prezzo (ovvero la somma dei prezzi) coincide qui con un prezzo di produzione che a sua volta eguaglia il valore, la terza ci apre la strada verso una serie di fenomeni il cui studio è di primaria importanza per la teoria marxista. Essa implica che il processo di formazione di un saggio medio del profitto non determina un corrispondente livellamento dei valori delle merci ai prezzi di produzione quando si pone un ostacolo alla libera migrazione dei capitali. Se prescindiamo dalle situazioni di monopolio vero e proprio, peraltro rare e limitate nel tempo, l'unico fattore che può porsi come ostacolo all'accumulazione di capitale in sfere caratterizzate da una composizione organica inferiore alla media, dunque da un elevato saggio del profitto, è costituito dalla proprietà privata della terra, in altri termini dalla proprietà fondiaria.
Oltre al lavoro ed ai mezzi di lavoro, la terra costituisce il terzo elemento fondamentale del processo produttivo per molte sfere di produzione, in primo luogo per l'agricoltura ma anche nel caso dell'industria mineraria ed in generale per tutte le materie prime. La proprietà fondiaria si pone qui come una forza estranea che limita l'investimento di capitale, imponendo delle condizioni che totalmente o in parte escludono il livellamento dei valori ai prezzi di produzione, quindi la trasformazione del plusvalore in profitto medio. Infatti, qualsiasi investimento di capitale che richieda l'uso di un terreno privato può essere effettuato solo dopo che quest'ultimo sia stato preso in affitto da parte di un capitalista, il quale pagherà al proprietario terriero una somma di denaro che viene detta rendita fondiaria, sia che si tratti di terreni coltivabili, sia nel caso di terreni edificabili, boschi, miniere, etc. Questa rendita viene sempre pagata per l'uso del terreno in sé, indipendentemente dal fatto che si trovi allo stato naturale oppure abbia già subìto dei miglioramenti in seguito alla coltivazione. Essa inoltre non può rientrare nei costi di produzione in quanto, al pari dell'acqua, del vento e di altre risorse naturali, la terra non costituisce il prodotto di alcuna sfera produttiva, per cui non vi è incorporato lavoro umano, dunque un valore. E tuttavia nella società borghese anche la terra appare come merce, e le si attribuisce un prezzo come se si trattasse di un prodotto del lavoro. Ciò è possibile in quanto, come ogni altro reddito monetario, la rendita può essere "capitalizzata", ovvero essere considerata come l'interesse di un capitale immaginario che assume qui la forma irrazionale di un "prezzo" della terra, pur essendo questa, ripetiamo, priva di valore. Se il saggio dell'interesse è, poniamo, pari al 5%, allora una rendita fondiaria annua di 10000 $ può essere considerata equivalente all'interesse di un capitale pari a 200000 $, il quale rappresenta così il "prezzo" di quel terreno. Ora, la tendenza storica del saggio del profitto a diminuire implica una altrettanto tendenziale diminuzione del saggio dell'interesse. Ma se il saggio d'interesse diminuisce dal 5 al 4% allora, usando le cifre dell'esempio precedente, una rendita annua di 10000 $ rappresenta ora l'interesse di un capitale maggiore, pari a 10000/0.04 = 250000 $. Pertanto, indipendentemente dai movimenti della rendita, il "prezzo" della terra è destinato storicamente a salire.
In definitiva, dunque, l'esistenza della proprietà privata terriera determina un ostacolo al livellamento del saggio del profitto in quanto impone alla classe dei capitalisti il pagamento di una rendita fondiaria che, non potendo rientrare nei costi di produzione, dunque nel prezzo di costo della merce, deve avere origine nel plusvalore stesso, ovvero deve costituirne una frazione. Di conseguenza quest'ultimo dovrà essere superiore al profitto medio. D'altra parte, ciò può verificarsi solo se il valore supera il corrispondente prezzo di produzione e se, parallelamente, il livello dei prezzi di questi prodotti si mantiene esso stesso al di sopra del prezzo di produzione. In seguito a questo meccanismo, una frazione spesso rilevante delle sfere che compongono il sistema di riproduzione, costituita da produzioni a bassa composizione organica ed elevato saggio del profitto, viene così ad essere costantemente sottratta al meccanismo di livellamento dei valori ai prezzi di produzione. Il prezzo di queste merci potrà dunque coincidere con il valore, oppure essere leggermente inferiore ad esso, ma comunque superiore al prezzo di produzione. Nel seguito, per semplicità supporremo sempre che la rendita sia costituita dalla differenza esatta tra valore e prezzo di produzione e non da una parte di questa differenza.
Per meglio comprendere l'influenza della proprietà fondiaria sul processo di accumulazione, con tutte le conseguenze che ne derivano, risulta conveniente suddividere il meccanismo di riproduzione in due grandi raggruppamenti di sfere: da un lato le sfere industriali che concorrono alla formazione del saggio medio del profitto, dall'altra le sfere soggette al vincolo della proprietà fondiaria, in particolare l'agricoltura. Nel seguito, per brevità ci riferiremo a quest'ultimo raggruppamento come al "settore delle materie prime", e le grandezze che ad esso si riferiscono verranno indicate con singoli o doppi apici.
Sia dunque τ' il saggio del profitto che si determinerebbe nel settore delle materie prime se il tutto il lavoro impiegato fosse lavoro semplice, dunque se il saggio del plusvalore coincidesse con il saggio generale del plusvalore S. Si ha chiaramente:
 (3.2)
(3.2)Poiché in base al nostro assunto Ω' < Ω, allora si ha che il saggio del profitto espresso dalla (3.2) risulta essere maggiore del saggio medio del profitto. In altri termini si ha che τ' > τ. Pertanto, se D' è il capitale anticipato per la produzione delle materie prime, allora il plusvalore che si ottiene soddisfa la relazione:
 (3.3)
(3.3)e il capitale merce prodotto avrà un valore pari a:
 (3.4)
(3.4)Qualsiasi capitale di grandezza pari a D', se investito nell'ambito dei settori industriali, otterrebbe invece dalla vendita dei prodotti al prezzo di produzione un plusvalore τD' inferiore. Chiamiamo rendita assoluta R' l'incremento di plusvalore che si ottiene per mezzo della vendita dei prodotti della terra al valore determinato dalla (3.4):
 (3.5)
(3.5)Questa rendita viene pagata dal capitalista affittuario al proprietario fondiario e costituisce la forma fondamentale di rendita fondiaria, nel senso che deve la sua esistenza alla sola proprietà privata della terra, dunque alla proprietà fondiaria in quanto tale, e non a fattori aggiuntivi che verranno presi in considerazione in seguito. Conveniamo inoltre di chiamare saggio della rendita assoluta la differenza tra il minimo saggio del profitto che può determinarsi nel settore delle materie prime ed il saggio medio del profitto, dunque la grandezza:
 (3.6)
(3.6)Il saggio della rendita assoluta determina evidentemente la grandezza assoluta della rendita che può ottenere un proprietario fondiario quando sul suo terreno viene investito un capitale di grandezza data. Infatti, combinando la (3.5) con la (3.6) si ha che R' può essere espresso come:
 (3.7)
(3.7)Notiamo ora che essendo τ' determinato dalla composizione organica dei capitali investiti nel settore delle materie prime, un'eventuale variazione del saggio medio del profitto lascia invariante la somma ρ + τ se il saggio generale del plusvalore non cambia. Pertanto, a una diminuzione del saggio medio del profitto deve corrispondere un proporzionale aumento del saggio della rendita assoluta, dunque della rendita stessa, e viceversa. Questa regola chiaramente presuppone variazioni di τ che non dipendono da mutamenti del saggio generale del plusvalore, ma solo da variazioni nella composizione organica media dei capitali industriali.
Nel paragrafo successivo vedremo come le differenze esistenti tra i diversi terreni generano una seconda forma di rendita e un ulteriore aumento dei prezzi delle materie prime al di sopra del prezzo di produzione.
3.2 - Rendita differenziale
Consideriamo una singola produzione agricola a vasta diffusione, quale potrebbe essere la produzione di caffè o grano. Supponiamo inoltre che il terreno coltivato complessivo sia suddiviso in n proprietà fondiarie di estensione A1,A2,..., An. A un dato grado di sviluppo della forza produttiva del lavoro, la quantità di capitale necessaria per la coltivazione di un terreno di estensione determinata è una costante che dipende solo dal tipo di coltivazione che si intende effettuare. Questa grandezza definisce la densità di capitale μ sul terreno messo a coltura.
Se A è l'estensione (in ettari) del terreno e D' rappresenta il capitale impiegato, allora per definizione avremo:
 (3.8)
(3.8)Nel caso in esame questa costante determina univocamente la grandezza dei capitali impiegati su ciascuno degli n terreni:
 (3.9)
(3.9)Consideriamo ora le quantità di produzione q'1, q'2,...,q'n che si ottengono al termine di un ciclo di riproduzione dall'applicazione di questi n capitali. Queste grandezze dipendono essenzialmente da tre fattori. In primo luogo dal grado di sviluppo della forza produttiva del lavoro agricolo, per cui variano in funzione del più o meno elevato grado di utilizzo di nuove macchine agricole, di fertilizzanti sofisticati, etc. La fertilità naturale dei terreni dipende dal contenuto di sostanze nutritive presenti negli strati superficiali del suolo. Ma il fatto che queste sostanze si trovino in una forma più o meno facilmente assimilabile, e quindi utilizzabile come nutrimento da parte delle piante, dipende dal grado di sviluppo della tecnologia chimica e meccanica in agricoltura, dunque dal grado di sviluppo delle forze produttive. In secondo luogo, esse dipendono dall'estensione dei rispettivi terreni, dunque dalle grandezze A1, A2,...,An. Infine, anche a parità di estensione del terreno messo a coltura ed impiego di mezzi di lavoro, concimi, etc. esse si differenziano in funzione del grado di fertilità del terreno, il quale dipende a sua volta dalle differenze di composizione chimica che si riscontrano in suoli diversi. Ora, poiché in base alla (3.9) il capitale che viene associato ad un terreno di estensione Ak è una grandezza determinata, il grado di fertilità di un terreno può essere espresso sia come rapporto tra la quantità di produzione ed il capitale investito, sia come la quantità di prodotti per unità di superficie. Nel seguito, ci riferiremo alla prima di queste due grandezze come al grado di fertilità dei terreni:
 (3.10)
(3.10)Analogamente, chiameremo fertilità naturale il rapporto:
 (3.11)
(3.11)Per la (3.9) queste grandezze sono legate dalla seguente relazione:
 (3.12)
(3.12)Supponiamo ora di voler determinare il valore di questi prodotti. In questo caso dovrà essere utilizzato un criterio che, come vedremo tra poco, differisce in modo sostanziale dalla determinazione del valore di mercato per i prodotti industriali. Consideriamo innanzitutto due capitali di uguale grandezza, A e B, impiegati in una stessa sfera di produzione del settore industriale. Supponiamo che inizialmente essi abbiano una composizione organica uguale alla composizione media e, utilizzando la stessa tecnica produttiva, ottengano un identico saggio del profitto mediante la vendita dei prodotti al prezzo di produzione, che in questo caso coincide con il valore individuale di produzione. Ad esempio, la situazione potrebbe essere inizialmente caratterizzata dai seguenti parametri:

In questo caso il valore del capitale merce sarebbe pari a 700 per entrambe le aziende, per cui il prezzo dei prodotti sarebbe dato da:

Supponiamo ora che ad un certo punto l'azienda B introduca una nuova tecnica produttiva, pur utilizzando lo stesso numero di operai. Ad esempio, il capitale costante CB potrebbe passare a 600 e simultaneamente la quantità di prodotti qB salire a 100 unità.
In questo caso il valore individuale dei prodotti dell'azienda B subirebbe un calo dato da:

Il valore individuale dei prodotti dell'azienda A resterebbe invece immutato. D'altra parte, per quanto riguarda il valore di mercato, esso è ora dato dalla media ponderata dei valori individuali uA e uB, in quanto in condizioni normali l'azienda A tenderà ad abbassare il prezzo di vendita per assicurarsi la vecchia quota di mercato, mentre l'azienda B, confortata dal fatto che la ditta concorrente offre i propri prodotti a un prezzo maggiore, tenderà da parte sua ad aumentare il prezzo al di sopra del valore individuale in modo da massimizzare i profitti. Il valore di mercato che si viene a stabilire dipenderà comunque dalle rispettive quantità di produzione. Infatti, esso si avvicinerà in misura maggiore al valore individuale delle merci prodotte in quantità superiore. Nel caso in esame avremo che u sarà dato da:

La vendita dei prodotti al valore di mercato u determina, nel caso dell'azienda B, la formazione di un plusprofitto, mentre A realizzerà un plusvalore inferiore a quello di partenza. Queste variazioni tra la massa di plusvalore prodotta ed il profitto effettivamente realizzato sono determinate dallo scarto esistente tra il valore di mercato ed il valore individuale dei prodotti. Nel caso delle aziende A e B avremo quindi:

La somma di queste variazioni è chiaramente nulla, essendo come è noto nulla la somma degli scarti dal valore medio. Il valore di mercato che si forma sulla base della determinazione esposta precedentemente costituisce il punto di equilibrio attorno al quale oscilleranno i prezzi di mercato in funzione della divergenza esistente tra domanda e offerta. In particolare, se la domanda è sostenuta, il prezzo di mercato si avvicinerà molto al valore individuale delle merci prodotte dall'azienda A, mentre l'azienda B, realizzando un capitale merce pari a 1000, otterrà un plusprofitto pari a 200 in aggiunta al profitto normale. Questo plusprofitto, è importante sottolinearlo, deve la sua esistenza al fatto che in queste condizioni il lavoro dell'azienda B si presenta come lavoro potenziato, cioè come lavoro che produce nello stesso tempo quantità superiori di valore, anche se gli operai di quest'azienda percepiscono come prima il salario normale. La determinazione del valore di mercato mediante una media ponderata dei valori individuali può chiaramente essere estesa al caso generale di una sfera produttiva in cui operano n aziende distinte. Se q1,q2,...,qn sono le quantità di produzione e u1,u2,...,un rappresentano i valori individuali, allora il valore di mercato sarà definito dall'espressione:
 (3.13)
(3.13)Pertanto, se q = q1 + q2 + ... + qn è la produzione totale, allora il valore complessivo prodotto da questo ramo d'industria sarà dato semplicemente da:
 (3.14)
(3.14)Infine, le variazioni tra le masse di plusvalore prodotte e i profitti realizzati saranno espresse dalle relazioni:
 (3.15)
(3.15)Nel caso generale di una sfera di produzione a composizione organica diversa dalla media il processo locale di formazione del valore di mercato si sovrappone al processo globale che porta alla formazione dei prezzi di produzione, per cui in condizioni di equilibrio o quasi-equilibrio sarà quest'ultimo a costituire il centro di oscillazione dei prezzi di mercato. D'altra parte, la concorrenza tende sempre ad uniformare il processo lavorativo nella maggior parte delle aziende che operano in una determinata sfera, per cui l'esistenza di sovrapprofitti dovuti a miglioramenti tecnici nel processo lavorativo costituisce sempre un fenomeno transitorio, che scompare non appena le nuove tecniche si diffondono tra i diversi produttori di quella merce particolare.
Torniamo ora all'esempio, precedentemente trattato, di una sfera di produzione agricola. In questo caso due terreni di uguale estensione, sui quali dunque sono stati impiegati capitali di uguale grandezza, forniscono una quantità di prodotti diversa se i gradi di fertilità differiscono tra loro. Pertanto, la diversità dei valori individuali è in questo caso da attribuire a fattori oggettivi esterni, legati alla composizione chimica dei terreni, piuttosto che a differenze tecniche tra i processi lavorativi. Inoltre, contrariamente a quanto avviene nelle sfere industriali, questa diversità non è chiaramente eliminabile. Ora, se il valore di mercato di questi prodotti fosse dato dalla media ponderata dei valori individuali u'1,u'2,...,u'n, il saggio del profitto τ' determinato dalla formula (3.2) potrebbe essere ottenuto solo dal capitale investito su di un terreno a fertilità intermedia, per il quale si avesse u'k = u'. Consideriamo infatti quattro capitali di diversa grandezza, impiegati su terreni a diversa fertilità. Ad esempio, potremmo avere una situazione come quella mostrata in tab. 3.1. Si suppone qui che i quattro capitali abbiano la stessa composizione e che il saggio del plusvalore coincida in ogni caso col saggio generale del plusvalore S, per cui il saggio del profitto di questa sfera è τ' = 10%. Ora, se il valore fosse determinato dalla media ponderata dei valori individuali u'i, dunque da un'espressione del tipo (3.13), si avrebbe u' ≅ 9.71 e gli scarti dalla media sarebbero dati da:

| Terreno | D' | P' | M' | φ | q' | u' |
|---|---|---|---|---|---|---|
| A | 1000 | 100 | 1100 | 0.105 | 105 | 10.48 |
| B | 1500 | 150 | 1650 | 0.110 | 165 | 10.00 |
| C | 1200 | 120 | 1320 | 0.113 | 136 | 9.71 |
| D | 2000 | 200 | 2200 | 0.120 | 240 | 9.17 |
Tab. 3.1 - Variazione dei prezzi individuali in funzione del grado di fertilità del terreno.
Si noti che il valore individuale dei prodotti associati al terreno C coincide con il valore medio u', per cui lo scarto δu'C è nullo.
Le variazioni tra plusvalore e profitto realizzato sarebbero quindi le seguenti:

Queste variazioni determinano chiaramente un saggio del profitto inferiore a τ' nel caso dei capitali che operano sui terreni A e B, mentre il capitale associato al terreno D otterrebbe un plusprofitto. Per quanto riguarda il capitale impiegato sul terreno C, esso sarebbe dunque l'unico ad ottenere esattamente il saggio del profitto τ'. È facile determinare la fertilità che deve avere un qualsiasi terreno X affinché il capitale investito su di esso ottenga esattamente il saggio del profitto τ' relativo a quella sfera di produzione. Infatti, essendo:

e posto u'x = u', allora chiamando φ* questa fertilità si ha che:
 (3.16)
(3.16)In definitiva se il prezzo di questi prodotti fosse determinato dai terreni a fertilità intermedia φ*, tutti i capitali operanti su terreni con fertilità φ > φ* otterrebbero un saggio del profitto superiore a τ', mentre quelli operanti su terreni a fertilità inferiore avrebbero un grado di redditività inferiore. D'altra parte, è facile rendersi conto che queste differenze si troverebbero immediatamente in contrasto con la natura del modo di produzione capitalistico. Infatti, come abbiamo visto nel paragrafo precedente, il saggio del profitto τ' di una sfera appartenente al settore delle materie prime deve coincidere con la somma tra il saggio medio del profitto ed il saggio della rendita assoluta (eq. 3.6). Pertanto, mentre un capitale associato ad un terreno con fertilità φ* riuscirebbe simultaneamente a realizzare un profitto medio pari a τD' ed a pagare una rendita assoluta R' = ρD' al proprietario fondiario, i capitalisti che operano su terreni a fertilità inferiore a φ* otterrebbero un profitto inferiore al profitto medio, e in casi estremi potrebbero addirittura non essere in grado di pagare la rendita dei rispettivi terreni. Inoltre, la perdita di profitto non potrebbe in questo caso essere eliminata, in quanto deve la sua origine a fattori oggettivi, indipendenti dunque dal modo di operare del capitale. Di conseguenza, terreni di questo tipo non potrebbero essere messi a coltura. Ciò dimostra che il valore dei prodotti della terra è soggetto ad una determinazione diversa rispetto ai prodotti del settore industriale. Infatti, la discussione precedente porta a concludere che il valore viene ora ad essere determinato dal valore individuale del terreno peggiore, in altre parole dal terreno a fertilità più bassa.
Tornando quindi al caso generale di una sfera in cui operano n capitali su altrettanti terreni a diversi gradi di fertilità, si ha che ciascun terreno, affinché possa essere messo a coltura, deve soddisfare la regola:
 (3.17)
(3.17)Infatti, la diseguaglianza (3.17) implica ora che, per ogni k, il valore di mercato del capitale merce sarà dato da:

Di conseguenza, un qualsiasi capitale ottiene ora nel peggiore dei casi un profitto medio in aggiunta alla frazione del plusvalore che si trasforma in rendita assoluta. Ciò accade chiaramente quando nella (3.17) vale il segno di uguaglianza, per cui imponendo che la grandezza φ* data dalla (3.16) rappresenti il grado di fertilità del terreno peggiore, in altri termini ponendo:
 (3.18)
(3.18)si ha che il valore u' dei prodotti di questa sfera sarà considerevolmente superiore alla media dei valori individuali. Per la (3.16) esso sarà infatti determinato dall'equazione:
 (3.19)
(3.19)La rendita assoluta si presenta dunque come la differenza tra il valore prodotto sul terreno peggiore ed il valore del capitale ivi investito aumentato del profitto medio. Per quanto riguarda invece i terreni a fertilità superiore, i capitali investiti ottengono in questo caso un plusprofitto tanto maggiore quanto più elevata risulta essere la fertilità dei rispettivi terreni. Questo plusprofitto non può tuttavia essere intascato dal capitalista, in quanto deriva da una caratteristica del terreno sul quale viene effettuata la produzione, e questo appartiene in generale ad una terza persona, ad un proprietario fondiario in grado di impedire o almeno ostacolare l'azione del capitale. Il plusprofitto si trasforma così in una nuova forma di rendita, diversa però dalla rendita assoluta analizzata precedentemente. Infatti, quest'ultima deve la propria origine all'esistenza stessa della proprietà privata della terra, la quale ostacola o impedisce del tutto il processo di livellamento del valore al prezzo di produzione in determinate sfere produttive. Viceversa, nel caso che abbiamo appena analizzato delle differenze di fertilità, la proprietà fondiaria non è responsabile della formazione del plusprofitto, ma solo della sua conversione in una forma di rendita fondiaria, che per la sua origine viene così indicata col nome di rendita differenziale. Poiché il plusvalore realizzato dal capitale operante sul k-esimo terreno è dato da:
 (3.20)
(3.20)allora la rendita differenziale sul k-esimo terreno sarà data da:
 (3.21)
(3.21)Come si vede confrontando la (3.21) con la (3.19), la rendita differenziale scompare per quei terreni caratterizzati da una fertilità φk = φ*; in questo caso il lavoro si presenta come lavoro semplice ed il proprietario fondiario percepirà la sola rendita assoluta.
Infine, la rendita totale per questa sfera produttiva sarà data dalla somma tra la rendita assoluta R' (eq. 3.5) e le rendite differenziali sui singoli terreni. Se D' è il capitale complessivo investito in questa sfera allora si avrà:
 (3.22)
(3.22)dove q' = q'1+q'2+...+q'n = φ1D'1+φ2D'2 +...+φnD'n rappresenta la massa totale della produzione.
3.3 - Accumulazione nel settore delle materie prime
Utilizziamo, ancora una volta, una generica sfera di produzione agricola come punto di partenza per la costruzione di un modello del processo di accumulazione nelle sfere soggette al meccanismo della rendita. D'altra parte, anche se in modo leggermente diverso, giungeremmo alle stesse conclusioni sviluppando la teoria a partire dall'industria estrattiva o da altri rami secondari del settore delle materie prime. Le conclusioni che si otterranno avranno pertanto validità generale e saranno applicabili all'intero settore di produzione delle materie prime.
Sia quindi A la superficie totale del terreno coltivabile per un particolare tipo di produzione agricola. Se μ è la densità di capitale a un determinato grado di sviluppo delle forze produttive, la grandezza massima del capitale che può essere investito in questa sfera di produzione è una quantità fissa, che verrà modificata solo in seguito ad un cambiamento tecnico nel processo lavorativo.
| φ | Superficie | % A | % cumulativa |
|---|---|---|---|
| 120 | 30000 | 30.00 | 30.00 |
| 105 | 15000 | 15.00 | 45.00 |
| 97 | 5800 | 5.80 | 50.80 |
| 95 | 12200 | 12.20 | 63.00 |
| 93 | 15320 | 15.32 | 78.32 |
| 90 | 21680 | 21.68 | 100.00 |
Tab. 3.2 - Esempio di distribuzione della fertilità sui terreni coltivabili.
Supponendo dunque costante la forza produttiva del lavoro, per la (3.8) si ha che il capitale operante in questo ramo della produzione non potrà superare un valore pari a μA. Ciò pone chiaramente un limite relativo, transitorio, al processo di accumulazione non solo di questa sfera produttiva, ma dell'intero meccanismo di riproduzione. D'altra parte, vedremo che questo limite non viene mai raggiunto, in quanto intervengono altri fattori che impongono ad un certo punto un rinnovamento delle tecniche produttive. Supponiamo ora di effettuare una statistica dei diversi gradi di fertilità che si riscontrano sull'area totale coltivabile A, indipendentemente dalla posizione geografica dei singoli terreni che compongono questa superficie totale. Ad esempio, per una superficie totale pari a 100000 ettari, potremmo ricavare una distribuzione come quella rappresentata in tab. 3.2. La prima colonna di questa tabella contiene, in ordine decrescente, i diversi gradi di fertilità riscontrati, mentre la seconda e la terza colonna riportano, rispettivamente in ettari ed in percentuale della superficie totale, l'estensione dei terreni caratterizzati da quel grado di fertilità. Infine, nella quarta colonna sono state incluse le percentuali cumulative dei terreni con fertilità maggiore o uguale a quella della riga corrispondente.
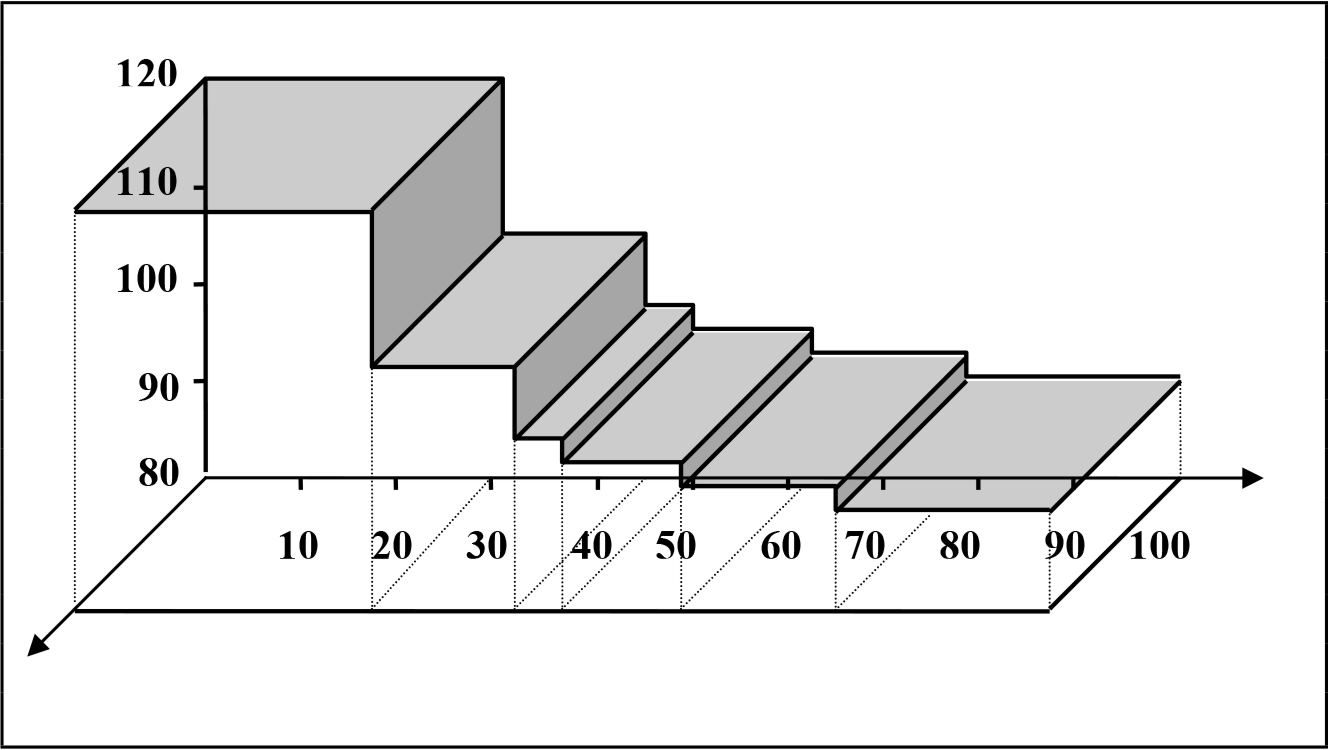 Fig. 3.1 - Grafico distribuzione di fertilità relativa ai dati di tab. 3.2.
Fig. 3.1 - Grafico distribuzione di fertilità relativa ai dati di tab. 3.2.Questo dato si ricava semplicemente sommando i numeri riportati nella terza colonna fino alla riga attuale. La stessa situazione può in alternativa essere rappresentata graficamente, considerando l'area totale A come un rettangolo di lati l ed h suddiviso in strisce trasversali a fertilità costante. Poiché l ed h possono assumere qualsiasi valore, a patto che si abbia l h = A, allora possiamo fissare arbitrariamente uno dei due parametri e determinare l'altro in modo che il loro prodotto fornisca proprio l'area totale A. In particolare, se poniamo h = 100 allora avremo che l = A/100, e la distribuzione di fertilità sul territorio considerato potrà essere messa in relazione diretta con le percentuali cumulative. Ad esempio, utilizzando i dati di tab. 3.2 si ottiene la distribuzione riportata in fig. 3.1.
Questo procedimento può essere generalizzato considerando la distribuzione φ come una funzione, non necessariamente continua, di due variabili sull'insieme rettangolare:

Le modalità costruttive della tabella assumono ora la forma di una condizione sulla funzione φ.
Essa dovrà essere monotona decrescente rispetto alla variabile x e costante rispetto a y:

In pratica, l'ultima condizione ci consente di considerare la distribuzione come una funzione della sola variabile x sull'insieme 0 ≤ x ≤ 100. Come vedremo tra poco, questo modo di trattare le variazioni di fertilità ci permetterà di rappresentare la produzione totale di plusvalore mediante un integrale facilmente calcolabile, piuttosto che mediante una sommatoria difficile da trattare.
Consideriamo ora lo svolgimento del processo di accumulazione nell'ambito di questa sfera di produzione. Supponiamo che inizialmente solo una frazione del terreno complessivo sia stata messa a coltura, e che quest'area coincida con l'insieme dei terreni a fertilità più elevata. Questa ipotesi si basa sulla constatazione che al termine di una crisi generale del settore delle materie prime, solo i capitali investiti sui terreni ad elevata fertilità possono sopravvivere al crollo dei prezzi che si verifica nel corso della crisi. Supponiamo infine che la formazione di nuovi capitali sia dovuta alla trasformazione in capitale addizionale del solo profitto medio e non dell'intero plusvalore prodotto. In altri termini, supponiamo che la rendita non venga a sua volta trasformata in capitale, ovvero che il proprietario fondiario non assuma esso stesso il ruolo di capitalista. In effetti, come avremo modo di vedere nel prossimo capitolo, la rendita gioca un ruolo attivo nel processo di accumulazione delle sole sfere industriali. Se dunque D'0 = D'(0) è il capitale operante all'inizio di una sequenza, allora dopo k cicli di riproduzione il capitale investito in questa sfera produttiva sarà dato da:
 (3.23)
(3.23)D'altra parte, questo accrescimento esponenziale del capitale implica una altrettanto rapida tendenza alla saturazione di tutto il terreno disponibile. Infatti, ad ogni nuovo ciclo il capitale operante verrà affiancato da nuovi capitali che provvederanno a soddisfare la domanda progressivamente crescente di queste materie prime da parte del settore industriale. Inoltre questo processo comporta la messa a coltura di terreni sempre meno fertili ed in misura sempre maggiore. Da un lato quindi, il prezzo di questi prodotti dovrà aumentare in quanto, come abbiamo visto nel paragrafo precedente, il valore delle materie prime è determinato dal valore individuale del terreno peggiore. Di conseguenza un nuovo terreno a fertilità inferiore potrà essere messo a coltura se e solo se la domanda sostenuta di questi prodotti provoca un aumento di prezzo tale che il nuovo terreno possa produrre un profitto medio in aggiunta alla rendita assoluta. D'altro canto, questo aumento dei prezzi sarà caratterizzato da una progressiva accelerazione, in quanto l'accumulazione di capitale richiede come abbiamo visto la messa a coltura di terreni sempre meno fertili in misura progressivamente crescente.
Calcoliamo ora la massa complessiva di plusvalore prodotta al k-esimo ciclo dal capitale D'(k). La massa di plusvalore che può essere prodotta dalla coltivazione di una generica striscia infinitesima posizionata alla coordinata x = ξ è data da:
 (3.24)
(3.24)dove u'(k) è il valore corrente di questi prodotti, dq'(ξ) rappresenta la produzione, in massa, di questa striscia e dD' è il capitale che opera in essa:
 (3.25)
(3.25)Ora, osservando la (3.10) si vede che la grandezza dq'(ξ) è determinata dal grado di fertilità locale della striscia e dal capitale impiegato:
 (3.26)
(3.26)Pertanto, la (3.24) può essere riscritta nella forma seguente:
 (3.27)
(3.27)Per ottenere la massa totale di plusvalore, basta ora tener conto che un capitale di grandezza pari a D'(k) si distribuisce su una frazione della superficie totale di lunghezza x(k) e larghezza l, per cui P'(k) sarà dato dall'integrale:

 (3.28)
(3.28)dove x(k) = D'(k)/μl. Si noti che questa formula determina implicitamente sia il valore totale della produzione che la sua massa. Infatti, si ha:
 (3.29)
(3.29) (3.30)
(3.30)Si noti che se invece della distribuzione dei gradi di fertilità avessimo a disposizione quella delle fertilità naturali, poiché per la (3.12) queste due grandezze sono proporzionali, potremmo in alternativa esprimere tutte le variabili fondamentali in funzione di γ(ξ):
 (3.31)
(3.31) (3.32)
(3.32)In ogni caso, una volta nota la distribuzione delle fertilità, il problema di determinare l'evoluzione delle variabili del processo di accumulazione si riduce essenzialmente alla valutazione dell'integrale:

in funzione del capitale operante D'(k). Per quanto riguarda il valore u'(k), esso per la (3.19) dipende dal minimo della distribuzione di fertilità sul territorio messo a coltura. Essendo per φ ipotesi una funzione monotona decrescente, avremo che:
 (3.33)
(3.33)per cui u'(k) sarà dato da:
 (3.34)
(3.34)Consideriamo ora, a titolo di esempio, una distribuzione lineare del tipo:
 (3.35)
(3.35)con m < 0. Il parametro φ0 = φ(0) rappresenta chiaramente la fertilità massima di questa distribuzione, che si riscontra per x = 0 (fig. 3.2).
Inserendo la (3.35) nella (3.34) e tenendo conto che:
 (3.36)
(3.36)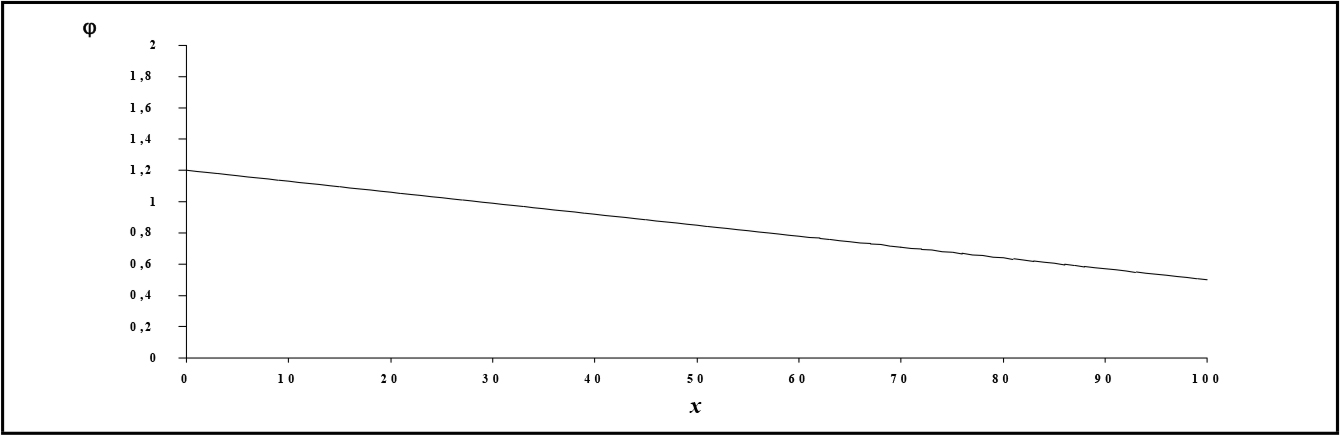 Fig. 3.2 - Esempio di distribuzione lineare delle fertilità.
Fig. 3.2 - Esempio di distribuzione lineare delle fertilità.si ha che il valore dei prodotti al k-esimo ciclo sarà dato da:
 (3.37)
(3.37)Chiaramente, essendo x ≤ 100, la (3.37) avrà significato solo per D'(k) ≤ 100μl = μA = D'max. La fig. (3.3) mostra la curva dei prezzi che si ottiene applicando la (3.37) ed utilizzando i parametri:

 Fig. 3.3 - Andamento del prezzo delle materie prime nel modello lineare.
Fig. 3.3 - Andamento del prezzo delle materie prime nel modello lineare.Questa curva mostra un andamento che corrisponde abbastanza bene a quello che abbiamo riscontrato nel capitolo precedente analizzando il grafico storico dell'indice dei prezzi delle materie prime (fig. 2.13). In particolare, il diagramma di fig. 3.3 si adatta bene all'andamento dei prezzi nei periodi 1900-1920, 1933-1952 e 1963-1980. Pertanto il modello lineare, nel quale come abbiamo visto si ha una crescita lenta dei prezzi seguita da una rapida esplosione, costituisce un valido punto di partenza per lo studio dei cicli di secondo ordine.
Consideriamo ora la massa della produzione. Inserendo la distribuzione (3.35) nell'integrale che compare nella (3.30) si ottiene:

 (3.38)
(3.38)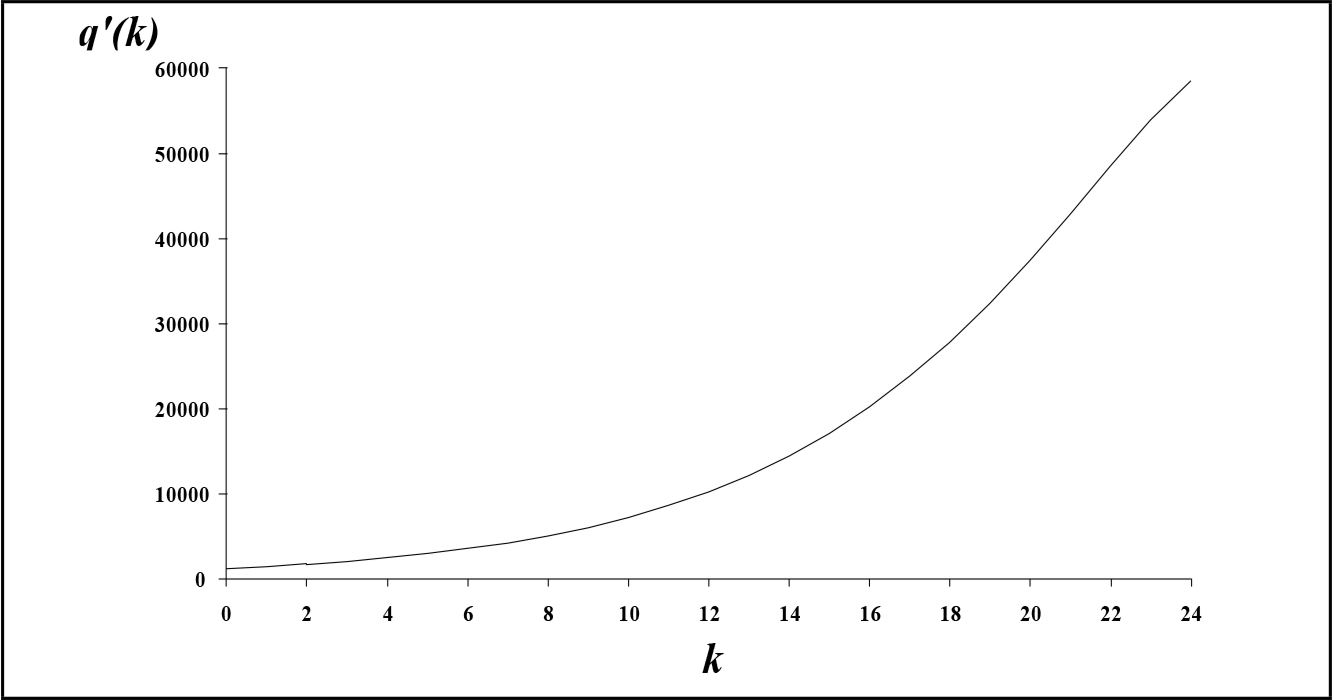 Fig. 3.4 - Andamento della massa della produzione nel modello lineare.
Fig. 3.4 - Andamento della massa della produzione nel modello lineare.L'andamento della curva q' = q'(k) è riportato in fig. 3.4. Si può osservare chiaramente la presenza di un flesso nella crescita della produzione, per cui tutta la parte finale della sequenza è caratterizzata da una diminuzione degli incrementi assoluti della massa della produzione. Anche in questo caso si ha un riscontro positivo tra l'andamento previsto teoricamente e le curve reali (si vedano ad es. i dati relativi alla produzione delle principali materie prime tra il 1950 ed il 1980, riportati in "World business cycles", London 1982).
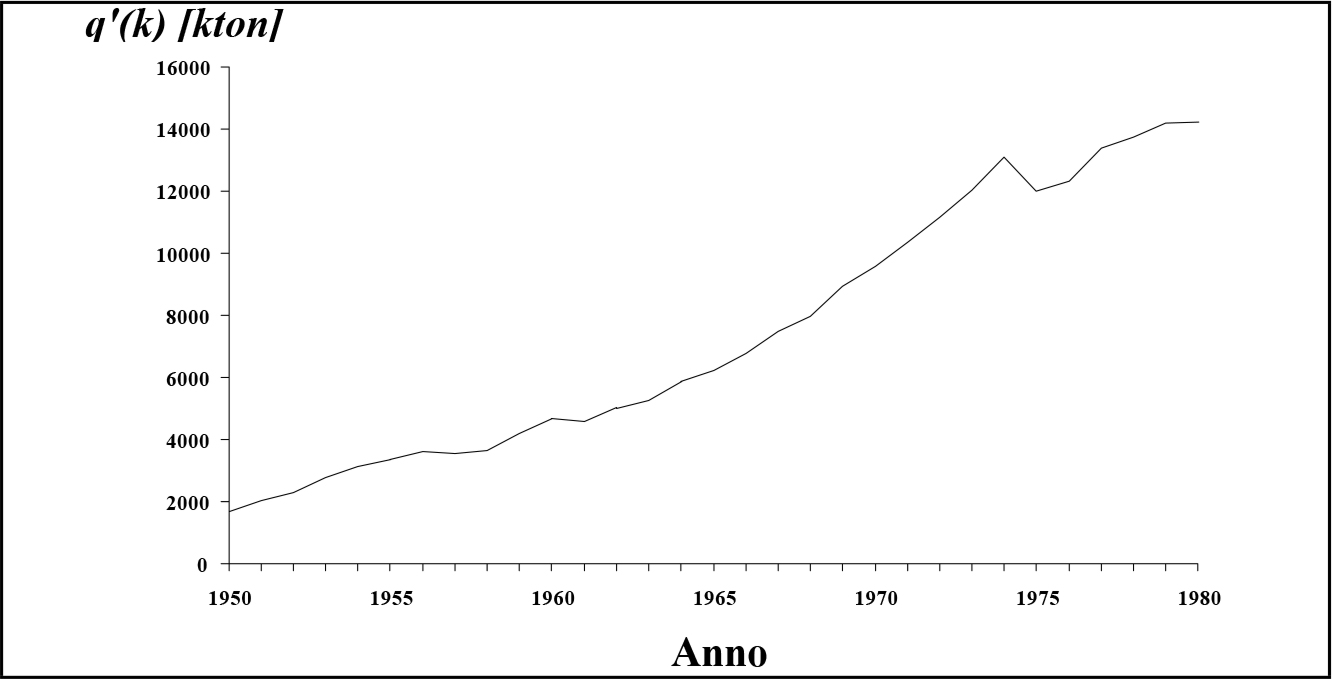 Fig. 3.5 - Alluminio: produzione mondiale 1950-1980.
Fig. 3.5 - Alluminio: produzione mondiale 1950-1980. Fig. Fig. 3.6 - Petrolio: produzione mondiale 1950-1980.
Fig. Fig. 3.6 - Petrolio: produzione mondiale 1950-1980.Nelle figure 3.5-3.8 sono riportati quattro esempi di crescita della massa della produzione, abbastanza facili da analizzare anche senza far ricorso a tecniche di regolarizzazione numerica. Questi grafici si riferiscono al periodo compreso tra il 1950 ed il 1980, dunque al terzo dei cicli di secondo ordine che hanno marcato la curva di accumulazione nel corso di questo secolo. Essi presentano caratteristiche simili, in particolare la presenza di un flesso attorno al 1970. Ciò costituisce una conferma definitiva della validità del modello. Infatti, una volta ricavate le funzioni u' = u'(k) e q' = q'(k) è semplice poi, applicando le formule esposte in questo paragrafo, ricavare tutte le altre grandezze significative del processo di accumulazione nella sfera considerata.
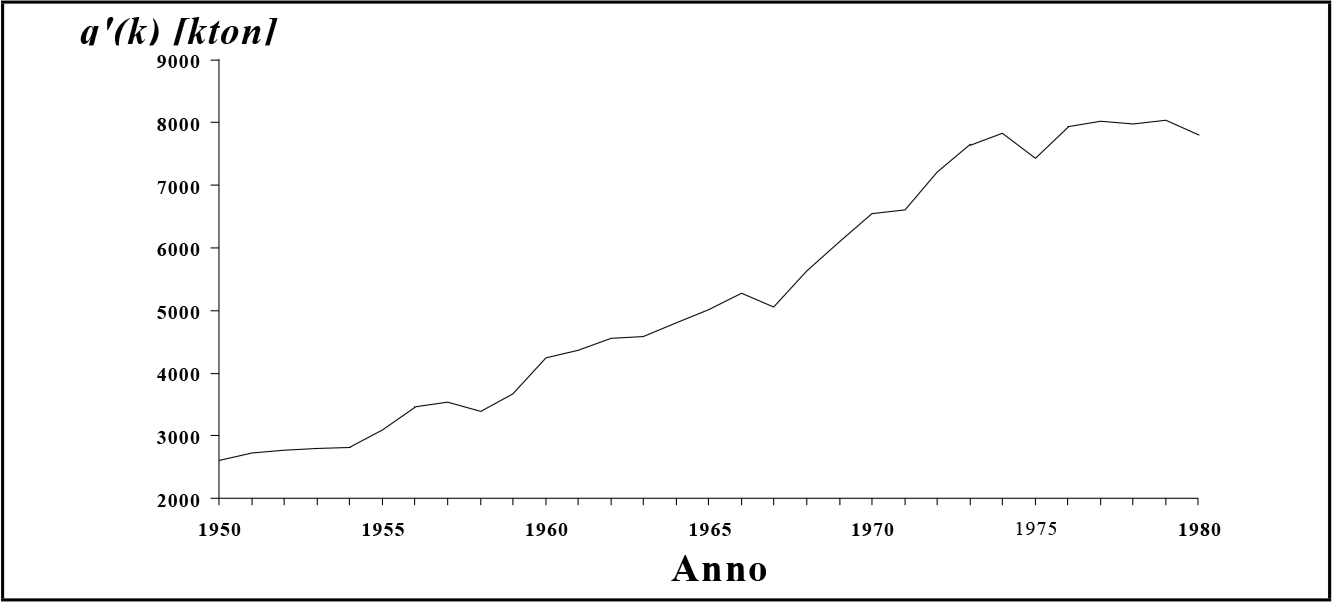 Fig. 3.7 - Rame: produzione mondiale 1950-1980.
Fig. 3.7 - Rame: produzione mondiale 1950-1980.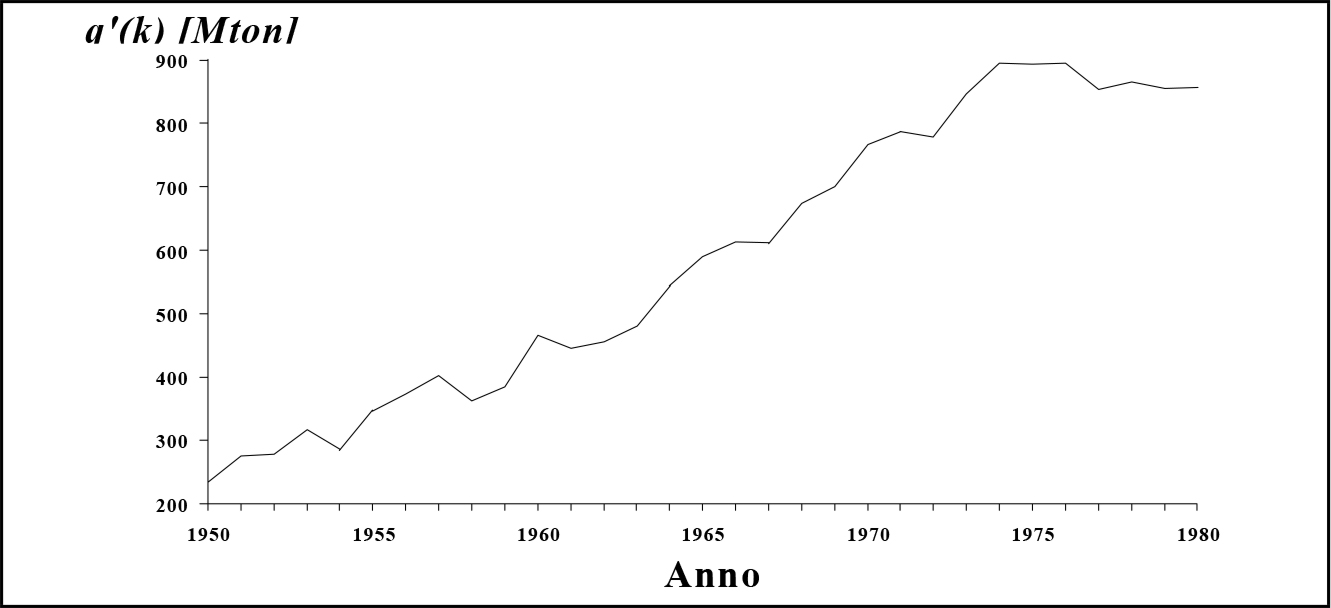 Fig. 3.8 - Minerali ferrosi: produzione mondiale 1950-1980.
Fig. 3.8 - Minerali ferrosi: produzione mondiale 1950-1980.Pertanto è su queste due curve che va ricercato un eventuale riscontro positivo tra modello e realtà. Nel caso in esame questo riscontro esiste, per cui siamo autorizzati ad assumere il modello lineare come valido punto di partenza per lo sviluppo della teoria dei cicli intermedi, che verrà trattata nel capitolo successivo.

Dinamica dei processi storici Volume I
Teoria dell'accumulazione
Quaderni di n+1.
Una formalizzazione spinta del sistema di riferimento marxista. In questo volume gli schemi di Marx vengono affiancati da una ulteriore dimostrazione poggiante su potenti strumenti matematici che confermano il carattere transitorio del capitalismo.

 n+1
n+1