Capitolo II. Le tendenze storiche del processo di accumulazione
2.1 - Equazioni del processo di accumulazione
Le tendenze storiche del processo di accumulazione del capitale sono il risultato di una lunga successione di cicli economici che mostrano l'alternanza di fasi di espansione, basate sulla riproduzione su scala allargata del capitale complessivo sociale, che si contrappongono a periodi più o meno lunghi di crisi sociale, innanzitutto economica, ma con riflessi più o meno marcati nella sfera sovrastrutturale, cioè sul piano della lotta di classe.
Ogni crisi interrompe bruscamente il precedente periodo di prosperità ed è il risultato delle contraddizioni materiali che permeano la società borghese, innanzitutto quelle che derivano dal carattere peculiare che in questa epoca assume il meccanismo della riproduzione materiale. Esso è costituito, come abbiamo visto nel capitolo precedente, da un vasto insieme di sfere di produzione, ciascuna delle quali comprende a sua volta un numero generalmente elevato di produttori indipendenti dello stesso tipo di merce.
Ognuna di queste sfere di produzione è collegata, attraverso il mercato, a diverse altre sfere produttive, per cui l'intero meccanismo assume la forma di un complesso intreccio di collegamenti nel quale ciascuno produce per gli altri ma indipendentemente dagli altri. In queste condizioni l'equilibrio dell'intero sistema si afferma solamente, ed in modo improvviso, violento, quando le tensioni accumulate superano una determinata soglia. Si comprende così come le crisi, con il loro potere distruttivo, rivoluzionario in senso borghese, sono anche un efficace meccanismo di regolazione e soluzione temporanea delle contraddizioni materiali. Nel corso di questi periodi la riproduzione, più che su scala allargata, si svolge su scala semplice e tutto il sistema produttivo viene più o meno sconvolto da una serie di ristrutturazioni che, con la violenta espulsione di migliaia di operai dal processo di produzione, con la conseguente sostituzione di macchine ad uomini ed automazione del processo lavorativo, fanno compiere alla forza produttiva del lavoro sociale un balzo in avanti e preparano il terreno per il successivo periodo di accumulazione.
Questo processo, più precisamente la sequenza di questi processi, porta tuttavia la società borghese a raggiungere, ad un certo punto, uno stadio in cui le forze produttive materiali entrano in contraddizione con i rapporti di produzione, giacché solo il lavoro può generare plusvalore e, come afferma Marx, due operai non potranno mai produrre il plusvalore che produrrebbero dieci operai, nemmeno se lavorassero 24 ore e si nutrissero di aria. Da un lato, dunque, la classe borghese riesce storicamente ad estrarre dal singolo lavoratore un plusvalore sempre maggiore, in quanto l'aumento della forza produttiva del lavoro sociale deve tradursi in una diminuzione del valore dei prodotti nei quali viene convertito il salario, dunque in una diminuzione del valore della forza lavoro.
D'altro canto è pur vero che la progressiva automazione del processo lavorativo determina, dopo ogni crisi, una diminuzione del numero di operai che un dato capitale è in grado di impiegare. Questa diminuzione agirebbe evidentemente in modo negativo sulla produzione complessiva di plusvalore se non fosse controbilanciata da un'estensione della scala della produzione. E in effetti la successione di cicli annuali di riproduzione su scala allargata che si verificano nel corso delle fasi di espansione successive alle crisi determina alla fine un ingrandimento della base produttiva della società. Ad un certo punto, comunque, la forza produttiva del lavoro raggiunge un livello tale che questa estensione non è più sufficiente a bilanciare la diminuzione relativa del numero di operai, ed inizia una fase storica caratterizzata dalla diminuzione assoluta, ciclo dopo ciclo, del numero di operai e della massa complessiva di plusvalore prodotta. In altri termini, a partire da questo momento l'aumento della popolazione operaia nel corso di ogni fase di espansione non compensa la diminuzione di operai che si verifica nel corso delle crisi. Con ciò si dimostra il limite reale ed assoluto del modo di produzione capitalistico, limite determinato dall'incompatibilità tra una società nell'ambito della quale pochi operai producono tanto plusvalore, e ad un certo punto diventano troppo pochi, con un insieme di rapporti di produzione basati sull'esistenza del plusvalore stesso.
Nelle pagine che seguono cercheremo di inquadrare il processo di accumulazione nel suo svolgimento storico, dimostrando al contempo l'esistenza di un punto limite al di la del quale la società borghese diviene antistorica, controrivoluzionaria, matura dunque per essere sostituita da una forma sociale più avanzata. Dimostreremo quindi che, al pari delle società che l'hanno preceduta, la società borghese raggiunge un punto oltre il quale i rapporti di produzione esistenti, da propulsori per lo sviluppo delle forze produttive, si trasformano in catene del progresso sociale. Questa prospettiva, basata sull'analisi del processo di accumulazione su lunghi periodi di tempo, sarà il risultato di una sequenza nell'ambito della quale i singoli cicli economici di espansione e crisi verranno considerati come eventi puntuali che marcano la traiettoria finale del processo di accumulazione. I risultati che si otterranno avranno perciò il carattere di curve tendenziali attorno alle quali oscilleranno le curve effettive. Per questo motivo non entreremo nei dettagli riguardo allo sviluppo dei singoli cicli economici; di questi considereremo per ora le sole caratteristiche generali.
Nel corso di questo capitolo cercheremo innanzitutto di formulare una legge quantitativa per lo svolgimento storico del processo di accumulazione capitalistica, alla luce dei risultati ottenuti nel capitolo precedente.
Consideriamo la storia del modo di produzione borghese come una sequenza ciclica di periodi di espansione della scala della produzione e di crisi. Tutte le grandezze di valore, come pure i tre rapporti di valore S, τ ed Ω, sono variabili che possono essere messe in relazione al generico ciclo k, visto come unità puntuale, piuttosto che ad un anno qualsiasi di espansione o recessione. Infatti, è abbastanza vicino alla realtà considerare che nel corso delle fasi di espansione la forza produttiva del lavoro resta sostanzialmente costante, per cui gli stessi rapporti di valore restano immutati e si ha semplicemente un'estensione della scala della produzione che dipende in generale dal numero di anni che compongono il ciclo e dal saggio medio del profitto nel corso dello stesso periodo. Questi periodi possono dunque essere descritti convenientemente mediante il meccanismo della riproduzione allargata di Marx. È in effetti la successiva fase di crisi che determina cambiamenti sostanziali nella forza produttiva del lavoro e quindi nei rapporti di valore. La crisi comporta inoltre una brusca interruzione del processo di accumulazione, per cui questa fase può essere rappresentata, come abbiamo visto, da un meccanismo di riproduzione su scala semplice.
Esprimiamo dunque tutte le variabili del problema come funzioni del parametro k, che rappresenta la combinazione di un periodo recessivo, caratterizzato dall'aumento generalizzato della forza produttiva del lavoro sociale, e del successivo ciclo di accumulazione associato ad una fase di espansione comprendente un numero arbitrario λ di anni. Ora, in base alle considerazioni svolte nel corso del capitolo precedente, sappiamo di poter determinare tutte le grandezze significative come espressioni di tre variabili fondamentali: la popolazione operaia n(k) impiegata all'inizio del ciclo k, la scala della produzione χ(k) relativa alla stessa fase ed infine il capitale costante per operaio Z(k).
Le formule che esprimono le grandezze ed i rapporti di valore in termini di n, χ e Z sono le seguenti:
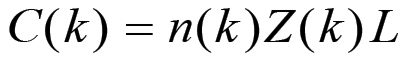 (2.1)
(2.1)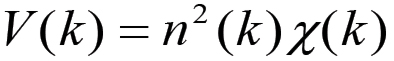 (2.2)
(2.2) (2.3)
(2.3)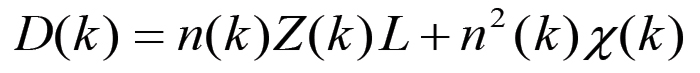 (2.4)
(2.4)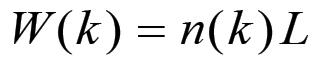 (2.5)
(2.5)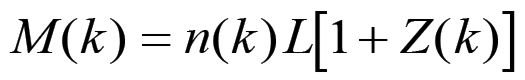 (2.6)
(2.6)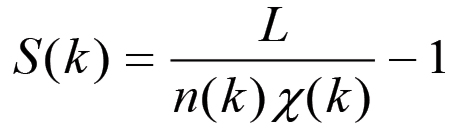 (2.7)
(2.7)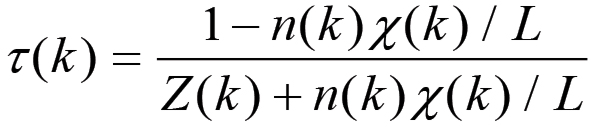 (2.8)
(2.8)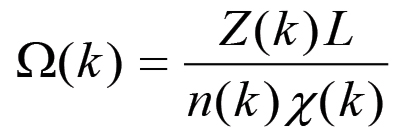 (2.9)
(2.9)Si noti che la formula (2.4) fornisce il capitale monetario anticipato D(k) = C(k) + V(k) all'inizio del primo anno corrispondente al ciclo k, mentre M(k) = C(k) + W(k) rappresenta (eq. 2.6) il valore del capitale merce prodotto nello stesso anno, in altre parole la produzione complessiva, in valore, nel corso del primo anno del ciclo di accumulazione k. Entrambe queste grandezze sono state espresse, come del resto tutte le altre, in funzione delle variabili n(k), χ(k) e Z(k), ovvero della popolazione operaia, della scala della produzione e del grado di sviluppo della forza produttiva del lavoro all'inizio del ciclo. Il fatto che tutte le espressioni relative alle grandezze di valore contengono queste tre sole variabili ci porta a concludere che le grandezze n(k), χ(k) e Z(k) costituiscono un set completo di variabili indipendenti che determina univocamente lo stato del sistema di riproduzione all'inizio di ogni ciclo.
Questa conclusione stabilisce che la terna [n(k),χ(k),Z(k)], in quanto definisce lo stato all'inizio del ciclo k, racchiude in se tutte le informazioni significative sul sistema. In altri termini, tutte le conclusioni che si possono trarre sul sistema al ciclo k costituiscono combinazioni algebriche delle variabili n(k), χ(k) e Z(k). Inoltre, la dinamica storica delle grandezze e dei rapporti di valore è definita una volta conosciuta la dinamica delle variabili di stato. Siamo ora in grado di determinare l'evoluzione dinamica degli stati del sistema come espressione del processo di accumulazione. Si tratta in sostanza di comprendere come evolve lo stato [n(k),χ(k),Z(k)] sotto l'azione combinata di un aumento della forza produttiva del lavoro e dell'estensione della scala della produzione causata dalla trasformazione del plusvalore prodotto nel corso dei vari anni del ciclo in capitale addizionale. A questo proposito, faremo l'ipotesi che tutto il plusvalore prodotto venga trasformato in capitale addizionale, dunque che ε sia uguale a zero in ogni sfera produttiva. In questo caso si ha una coincidenza tra saggio di accumulazione e saggio del profitto che non solo semplificherà notevolmente il problema, ma determinerà una dimostrazione della transitorietà del modo di produzione borghese nelle condizioni a lui più favorevoli, cioè in presenza di un'accumulazione portata avanti avendo a disposizione l'intero plusvalore prodotto e non una sua frazione. Consideriamo dunque il processo storico di accumulazione come unità di due movimenti elementari: sviluppo delle forze produttive da una parte, estensione della scala della produzione dall'altra. La transizione di stato:
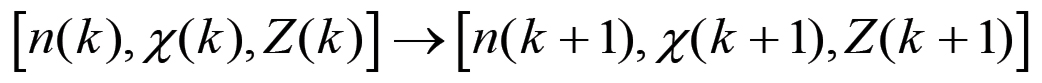 (2.10)
(2.10)associata all'insieme di questi due movimenti può essere determinata studiando separatamente, e poi combinando assieme, l'effetto di ciascuno dei due processi elementari sulle variabili di stato. In questo modo potremo esprimere le variabili di stato relative al ciclo successivo k+1 in funzione dei valori che esse assumono nel corso del ciclo k.
Consideriamo innanzitutto un aumento della forza produttiva del lavoro quando il sistema si trova nello stato [n(k),χ(k ),Z(k)]. Sia G > 1 il saggio di sostituzione di macchine ad uomini, cioè il fattore d'incremento delle variabili F e Z; se G = 1.05 allora queste grandezze subiranno un aumento del 5%, con G = 1.1 si avrà un aumento del 10%, e così via. L'effetto di questo incremento sulle variabili n, χ e Z è già stato studiato nel capitolo precedente, per cui sappiamo che determina il passaggio dallo stato [n(k),χ(k ),Z(k)] allo stato [n'(k),χ'(k), Z'(k)], definito dalle seguenti equazioni:
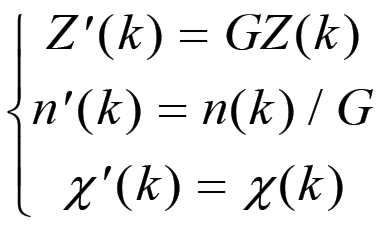 (2.11)
(2.11)La prima di queste equazioni dice che il capitale costante per operaio aumenta esattamente come F; la seconda calcola la corrispondente diminuzione di n tenendo conto che si tratta di una trasformazione che non altera la scala della produzione; la terza, infine, stabilisce semplicemente che la scala della produzione è costante sotto trasformazioni causate da un aumento della forza produttiva del lavoro. In base a queste tre equazioni ed alla (2.4) si ha dunque che nell'anno immediatamente successivo al termine della crisi il capitale anticipato D(k) sarà diminuito al valore D'(k).
Quest'ultimo sarà dato da:
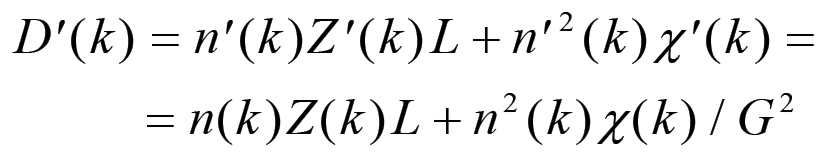 (2.12)
(2.12)Consideriamo ora, a partire dallo stato [n'(k),χ'(k ),Z'(k)], l'ampliamento della scala della produzione generato dalla trasformazione del plusvalore P(k) in capitale addizionale. Sia A(k) il fattore di espansione. In base alle considerazioni svolte nel capitolo precedente (eq. 1.93) si ha:
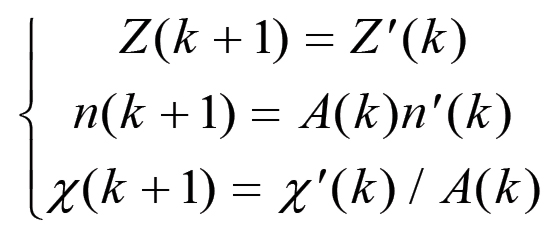 (2.13)
(2.13)Combinando assieme le trasformazioni (2.11) e (2.13) si ottengono infine le equazioni associate alla trasformazione completa (2.10):
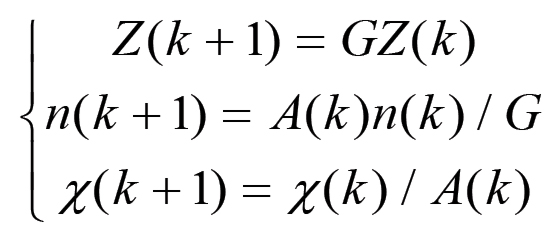 (2.14)
(2.14)Si noti che la forma delle equazioni (2.14) è indipendente dal fatto che si consideri prima una fase di aumento della forza produttiva del lavoro, mantenendo costante la scala della produzione, e poi un'estensione di questa con rapporti di valore costanti.
Si otterrebbero infatti le stesse equazioni (2.14) considerando il ciclo come il prodotto di un periodo di espansione seguito da una fase di crisi.
In quest'ultimo caso dovremmo combinare una espansione iniziale rappresentata da una trasformazione del tipo:
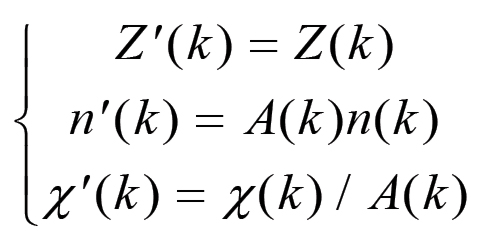
con un periodo di crisi rappresentato dalle equazioni:
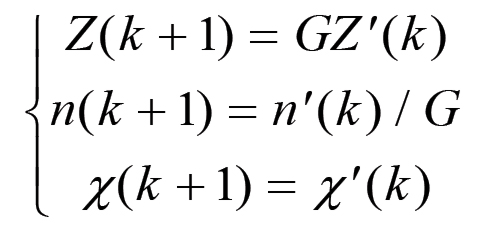
È facile verificare che la concatenazione di questi due gruppi di trasformazioni porta alle stesse equazioni (2.14). Comunque, questi due modi di considerare il processo di accumulazione portano a due sequenze diverse, in quanto il fattore di espansione A(k) come vedremo tra poco assume un valore diverso nei due casi. In effetti, nel primo caso noi partiamo dal punto culminante di una fase di espansione ed associamo l'inizio del ciclo ad un periodo di crisi che sfocia subito dopo in un'espansione della base produttiva. Pertanto il ciclo termina con un massimo che corrisponde al nuovo stato [n(k+1),χ(k+1),Z(k+1)]. La sequenza che si ottiene rappresenta così la successione dei massimi associati ad ogni ciclo economico, in altri termini la successione dei picchi positivi del processo di accumulazione. Viceversa, quando si considera il ciclo come la concatenazione di una fase di espansione con una fase di crisi, il punto di partenza coincide con la fine di un periodo di stagnazione, per cui la sequenza rappresenta una successione di picchi negativi, cioè di minimi relativi, del processo storico di accumulazione.
Si tratta ora di calcolare il fattore di espansione A(k) relativo alle due sequenze. Nel primo caso bisogna tener conto che la fase di espansione della base produttiva è rappresentata dalla trasformazione:
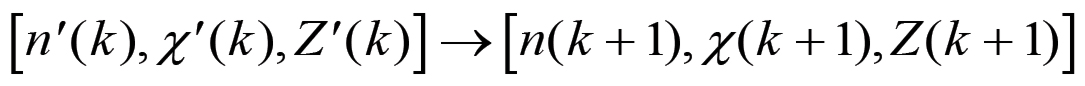 (2.15)
(2.15)per cui, utilizzando le eq. (2.13), il capitale anticipato diventa:
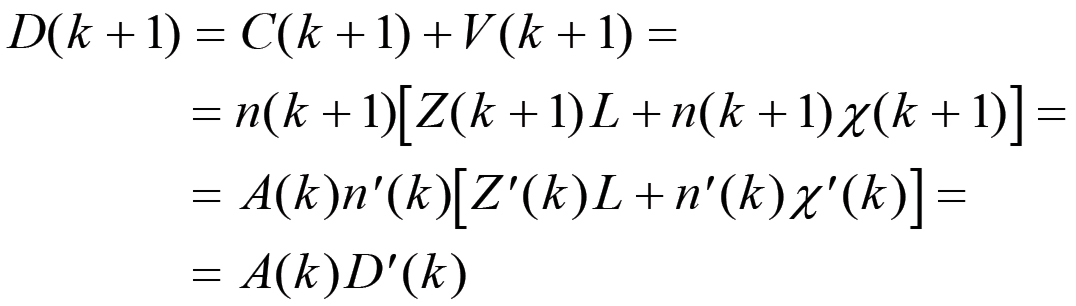 (2.16)
(2.16)La (2.16) si ricava immediatamente tenendo conto che in una trasformazione del tipo (2.13) il valore della forza lavoro v = nχ e la forza produttiva Z sono invarianti, in quanto un'estensione della scala della produzione per definizione non altera il valore della forza lavoro ed il capitale costante per operaio. Ora, D(k+1) è dato dalla capitalizzazione del plusvalore nel corso di ciascuno dei anni λ di riproduzione su scala allargata a partire dal capitale iniziale D(k). Consideriamo innanzitutto il caso più semplice in cui λ = 1, in altri termini fasi di espansione della durata di un anno. In questo caso si ha che:
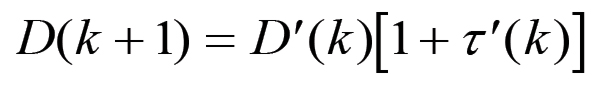 (2.17)
(2.17)È semplice ricavare ora il fattore di espansione A(k). Infatti, confrontando la (2.17) con la (2.16) si ha:
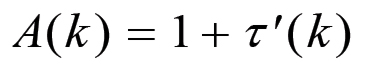 (2.18)
(2.18)per cui, utilizzando la (1.96) e le equazioni di trasformazione (2.11) si ha infine:
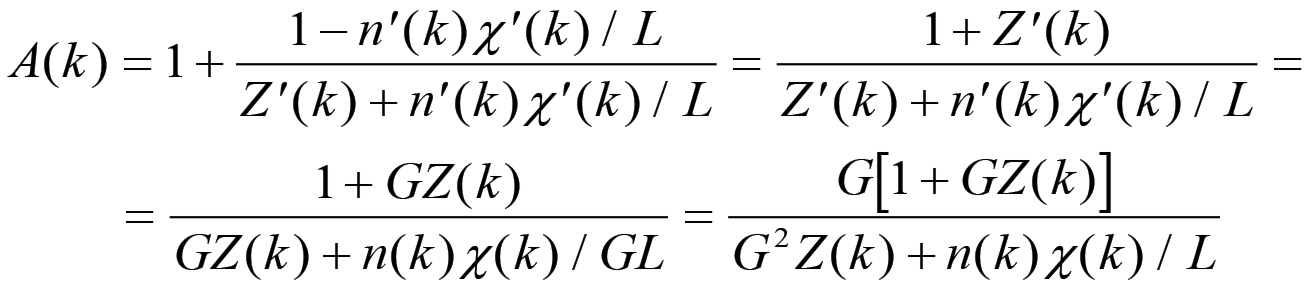 (2.19)
(2.19)Siamo finalmente in grado di combinare i due movimenti fondamentali che costituiscono il processo di accumulazione capitalistica in un unico movimento che tiene conto sia dello sviluppo delle forze produttive che dell'estensione della scala della produzione causata dalla trasformazione del plusvalore in capitale addizionale. Le equazioni precedenti ci consentono infatti di determinare la trasformazione diretta (2.10) come combinazione tra la trasformazione particolare [n(k),χ(k),Z(k)] → [n'(k),χ'(k),Z'(k)] e quella [n'(k),χ'(k),Z'(k)] → [n(k+1),χ(k+1),Z(k+1)]. Combinando infatti le equazioni (2.14) con la (2.19) si ottengono infine le seguenti tre equazioni fondamentali, relative al caso λ = 1:
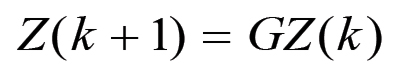 (2.20)
(2.20)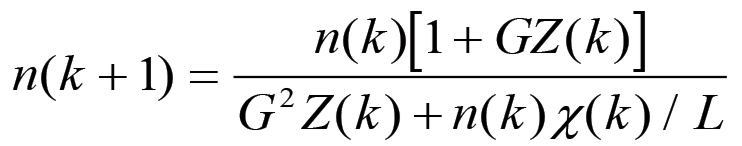 (2.21)
(2.21) (2.22)
(2.22)Queste tre equazioni ricorsive determinano lo stato successivo, cioè lo stato del sistema produttivo durante il ciclo successivo, in funzione dello stato attuale e dei parametri G ed L. Pertanto, se sono noti G ed L, le equazioni (2.20), (2.21) e (2.22) ci consentono di determinare immediatamente tutte le grandezze ed i rapporti di valore durante il ciclo successivo.
Consideriamo ora il caso λ > 1. Per λ > 1 il capitale monetario sociale si accresce, dopo λ anni, al valore:
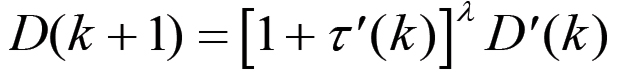 (2.23)
(2.23)Pertanto in questo caso il fattore di espansione A(k) assumerà il valore:
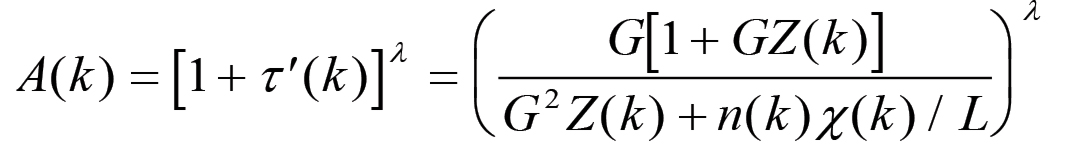 (2.24)
(2.24)Passiamo ora alla sequenza rappresentata dai picchi negativi. In questo caso l'estensione della base produttiva avviene nella fase iniziale del ciclo ed è rappresentata dalla trasformazione:
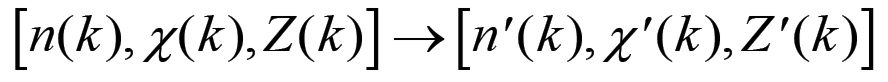 (2.25)
(2.25)Pertanto il capitale monetario, per λ = 1, sarà dato semplicemente da:
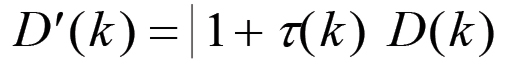
Il calcolo procede ora come nel caso precedente. Si ha:
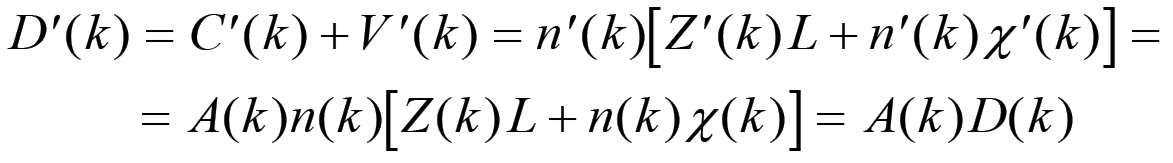 (2.26)
(2.26)Pertanto, otteniamo la seguente espressione per il fattore di espansione:
 (2.27)
(2.27)Le tre equazioni di trasformazione degli stati assumono quindi la forma:
 (2.28)
(2.28)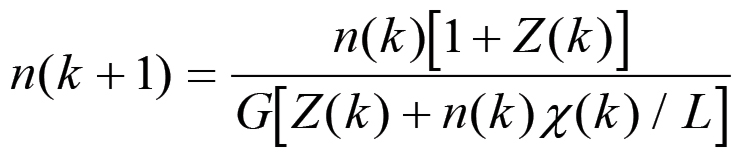 (2.29)
(2.29)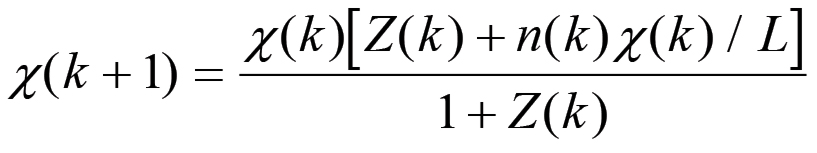 (2.30)
(2.30)Infine, per λ > 1 avremo che il fattore di espansione A(k) sarà dato da:
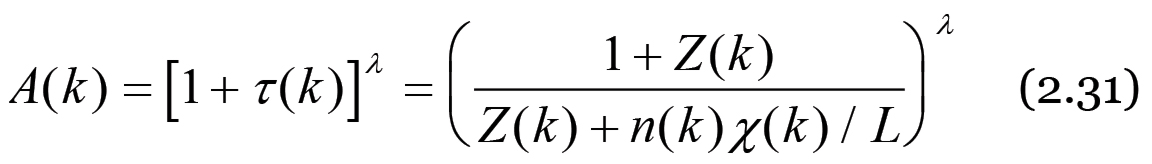 (2.31)
(2.31)Le equazioni precedenti mostrano che l'evoluzione storica del modo di produzione capitalistico è determinata essenzialmente dal valore che assumono i due parametri L e G, dunque dalla durata della giornata lavorativa e dal tasso di sostituzione di macchine ad uomini, ovvero dal saggio d'incremento della forza produttiva del lavoro. Entrambi questi parametri sono indipendenti dall'evoluzione delle variabili del sistema, per cui non possono essere ricavati teoricamente. I valori che essi assumono in un dato periodo storico possono invece essere osservati empiricamente e determinano in definitiva il tempo richiesto al modo di produzione borghese per passare da uno stato iniziale arbitrario ad un qualsiasi stato successivo.
È facile comprendere che sia L che G sono parametri di natura sovrastrutturale, legati cioè alla dinamica dei conflitti sociali tra le classi che compongono la società borghese. In quanto tali, queste grandezze esprimono la forza della interazione tra struttura e sovrastruttura della società. L'aumento oppure la diminuzione della durata della giornata lavorativa, il numero di operai che vengono licenziati nel corso di una crisi, la compressione dei salari che si verifica in questi periodi, etc., sono tutti fenomeni la cui entità dipende dall'equilibrio che si viene di volta in volta ad instaurare nell'ambito dello scontro tra le classi. Pertanto non solo una variazione di L, ma anche una variazione della forza produttiva del lavoro sociale, dunque un valore di G diverso dall'unità, sono il risultato di una lotta più o meno aspra tra le classi.
Una classe non è caratterizzata dalla semplice uniformità nella fonte dei redditi dei suoi elementi (ad esempio, salario, profitto, rendita, etc.) ma da un interesse generale che si contrappone sempre e comunque, in misura più o meno grande nel tempo, agli interessi materiali legati ad ogni altra fonte di reddito. Questa contrapposizione non può che tradursi nell'azione più o meno organizzata, più o meno efficace, talvolta anche violenta, di una classe contro tutti gli altri gruppi sociali che rappresentano interessi antagonisti. Ciò nonostante, è possibile che in certi contesti geostorici si verifichi una situazione transitoria di pace sociale a seguito di una temporanea comunanza di interessi tra gruppi sociali distinti, persino tra lavoratori salariati e borghesi; in questo caso il termine "classe" potrà essere utilizzato solo per esprimere una dinamica potenziale, dunque non ancora effettiva.
In generale, dunque, ogni gruppo sociale caratterizzato da un'uniformità di interessi non costituirà una classe se il suo interesse generale sarà in qualche modo legato ad altre fonti di reddito, dunque all'affermazione di altri interessi materiali. Nella società capitalistica esistono solo tre grandi classi potenziali: il proletariato, la borghesia ed i proprietari fondiari, legate rispettivamente al salario, al profitto ed alla rendita; gli altri gruppi sociali non costituiscono dunque delle vere classi (nemmeno la piccola borghesia). Nonostante ciò essi possono influire, in certi momenti, sui rapporti di forza che si vengono a stabilire in seguito alla contrapposizione di interessi tra le tre grandi classi sociali. In definitiva, è proprio l'equilibrio che si viene a creare nei rapporti tra questi grandi gruppi sociali in movimento, specialmente nel corso dei periodi di crisi, che determina di volta in volta il grado di aumento della forza produttiva del lavoro sociale, dunque il valore del parametro G, e l'eventuale variazione del parametro L.
Queste considerazioni ci portano ad attribuire un significato profondo alla grandezza G, in quanto essa rappresenta un indice dell'intensità dello scontro tra le classi sociali in un determinato periodo storico: valori elevati di G saranno il prodotto di fasi di fermento sociale, guerre, conquiste, ma anche vittorie del profitto sulla rendita, mentre valori di G prossimi ad 1 saranno caratteristici di periodi di relativa calma sociale e stabilità del sistema produttivo. Malgrado queste oscillazioni, da un punto di vista storico la società borghese non può fare a meno di sviluppare la forza produttiva del lavoro sociale, se non altro perché la terra e le altre risorse naturali hanno un limite assoluto finito. Pertanto, se consideriamo la grandezza G in una prospettiva storica, essa sarà sempre maggiore di 1 e la lotta di classe determinerà di volta in volta il valore che potrà assumere.
2.2 - Soluzione generale delle equazioni
Intendiamo ora studiare l'andamento della curva di accumulazione che si ricava a partire dalle equazioni di stato. Per "curva dell'accumulazione" intendiamo il grafico della funzione M = M(k), cioè il diagramma che esprime la tendenza storica della produzione, in termini di valore, in funzione del numero di cicli di accumulazione a partire da uno stato iniziale qualsiasi.
La curva rappresentata in fig. 2.1 è stata ricavata utilizzando i seguenti parametri: G = 1.23, λ = 10 ed L = 300 gl. In altri termini abbiamo supposto un incremento del 23% per la forza produttiva del lavoro nel passaggio da un ciclo a quello successivo, una durata media dei cicli pari a 10 anni ed un numero di giornate lavorative pari a 300 per anno. Inoltre, abbiamo assunto come stato iniziale la terna: n(0) = 100000 operai, χ(0) = 0.0022, Z(0) = 2.83. La curva riportata in fig. 2.1 si riferisce alla serie dei massimi relativi, e mostra chiaramente un flesso nel 13° ciclo, ovvero dopo 130 anni a partire dallo stato iniziale. A partire da questo punto si osserva che la produzione totale, da un ciclo all'altro, presenta incrementi sempre più piccoli.
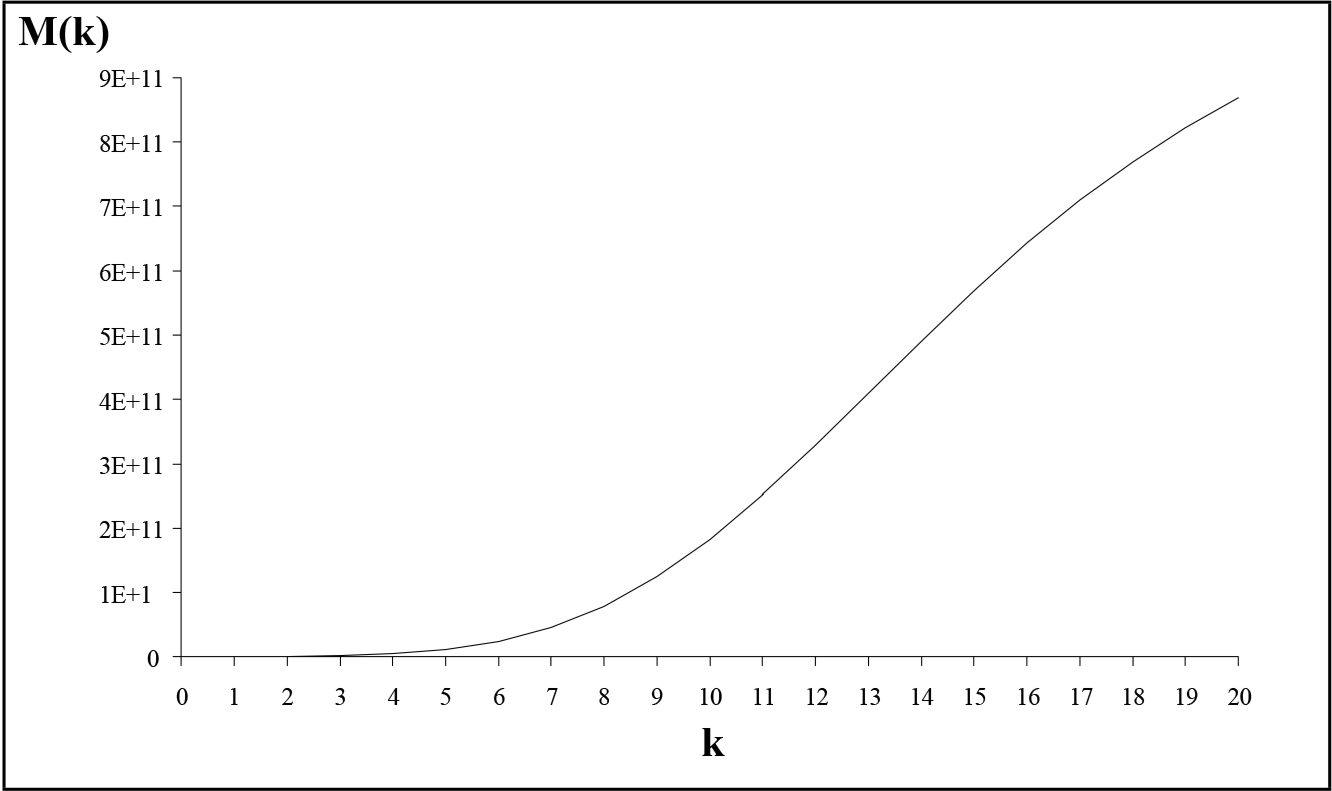 Fig. 2.1 - Produzione complessiva: serie dei massimi relativi.
Fig. 2.1 - Produzione complessiva: serie dei massimi relativi.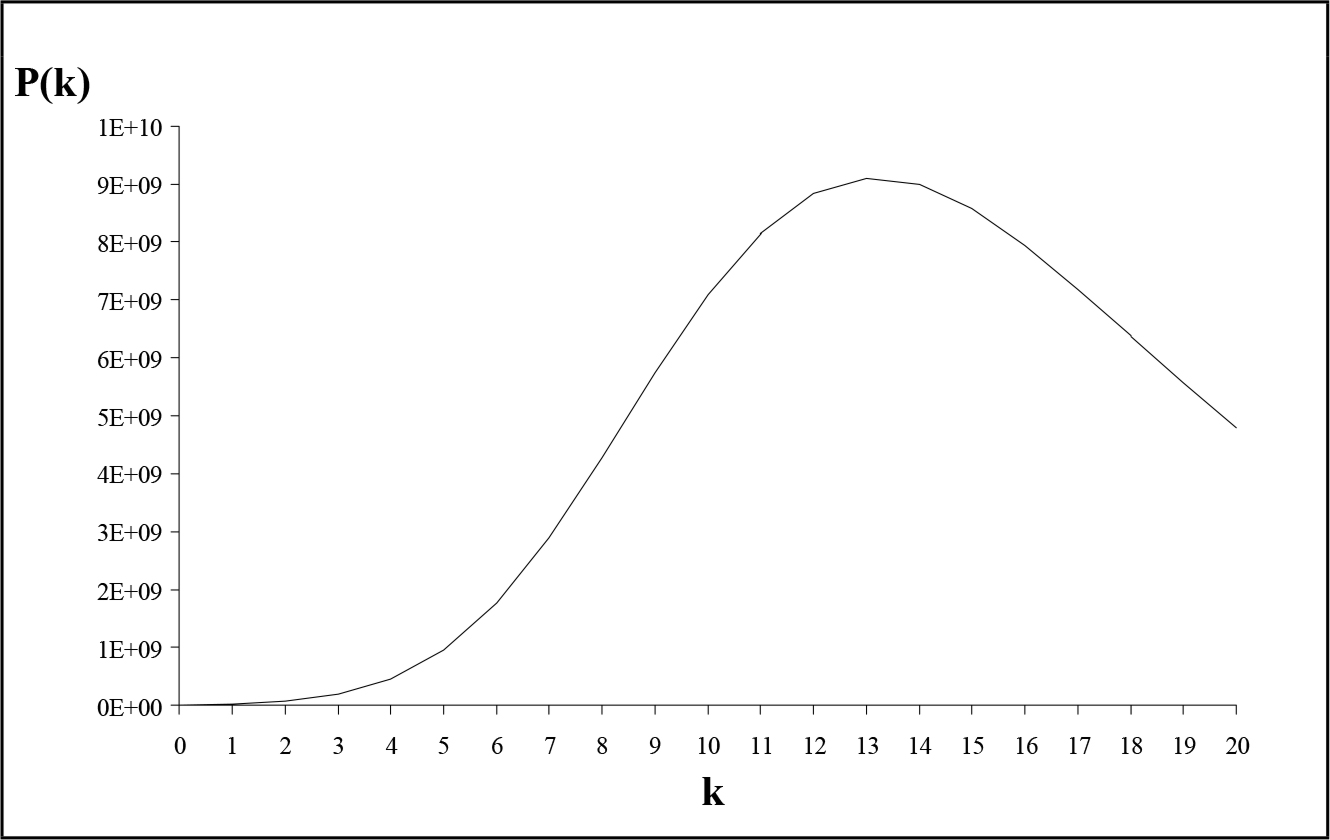 Fig. 2.2 - Tendenza storica della massa del plusvalore.
Fig. 2.2 - Tendenza storica della massa del plusvalore.Come vedremo tra poco, questo andamento non dipende dai valori iniziali e dai parametri selezionati, e può essere osservato, in modo più o meno netto, comunque vengano scelti questi valori. Il 13° ciclo mostra però anche un altro fenomeno, in quanto per questo valore di k le curve del plusvalore complessivo contenuto nel capitale M(k) e della popolazione operaia occupata mostrano un massimo (fig. 2.2 e 2.3). In altre parole, a partire da questo punto la massa di plusvalore e la popolazione operaia occupata si riducono progressivamente, ciclo dopo ciclo, anche se nell'ambito delle singole fasi di espansione interne ai cicli stessi subiscono un temporaneo aumento.
 Fig. 2.3 - Tendenza storica della popolazione operaia occupata.
Fig. 2.3 - Tendenza storica della popolazione operaia occupata.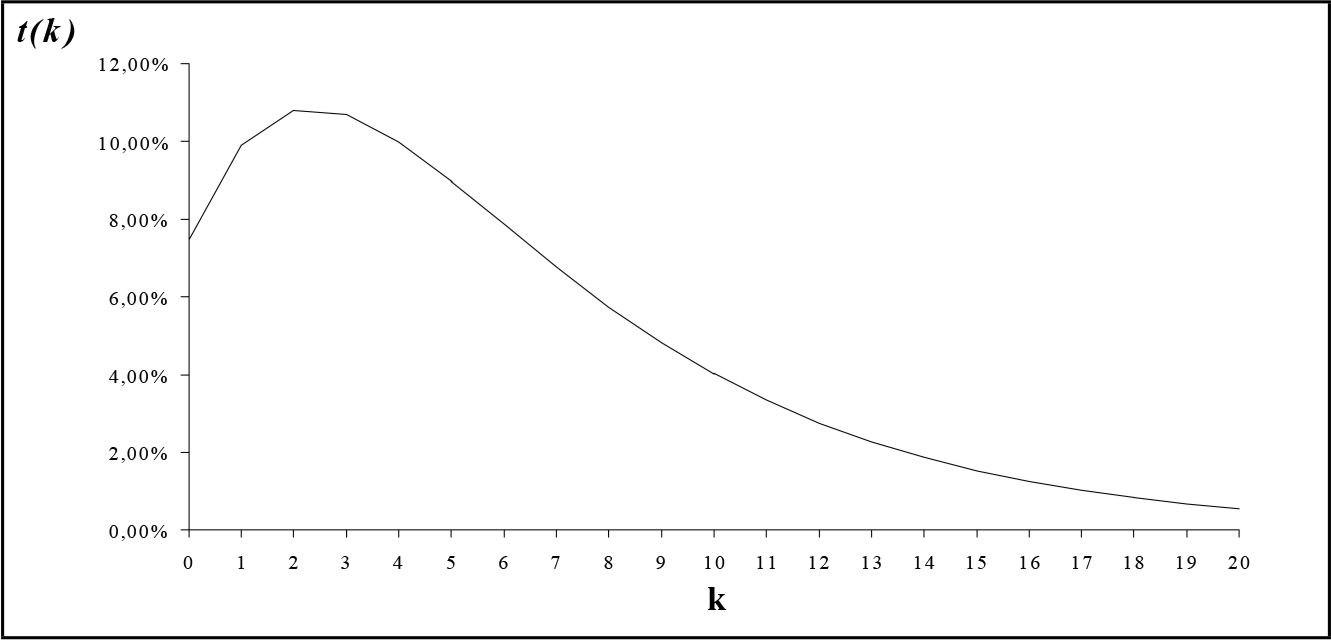 Fig. 2.4 - Saggio tendenziale di accumulazione.
Fig. 2.4 - Saggio tendenziale di accumulazione.Ciò accade perché a partire dal 13° ciclo la riduzione della popolazione operaia che si verifica nel corso delle crisi non compensa l'aumento relativo alla precedente fase di espansione. Infine, è possibile tracciare il grafico del saggio tendenziale di accumulazione (che nel nostro caso coincide con il saggio del profitto). Questa curva è riportata in fig. 2.4 e mostra un massimo iniziale al 2° ciclo seguito da una caduta progressiva ed irreversibile.
I risultati precedenti possono in ogni caso essere previsti teoricamente a partire dalle equazioni (2.14). Consideriamo la serie dei massimi relativi e poniamo per semplicità λ = 1. In questo caso il fattore di espansione A(k) sarà dato dalla (2.19). Per quanto riguarda la popolazione operaia, essa avrà un massimo per:
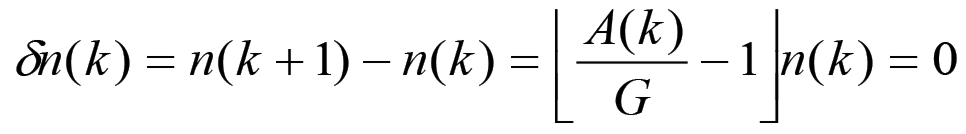 (2.32)
(2.32)Come risulta chiaramente da questa espressione, la curva n = n(k) è crescente (δn(k) > 0) solo per valori di A(k) tali che A(k) > G. Consideriamo ora il valore della forza lavoro v. Esso, in base alle eq. (2.14), evolve secondo la legge:
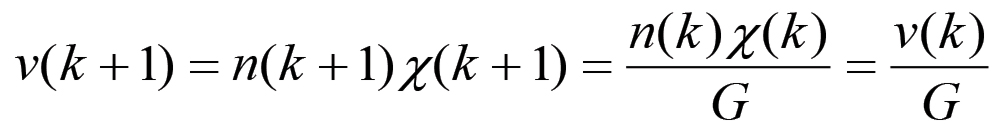 (2.33)
(2.33)Questa equazione ricorsiva può essere immediatamente risolta se è nota la condizione iniziale v0 = v(0). Si ha:
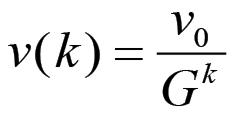 (2.34)
(2.34)Analogamente, le equazioni (2.14) mostrano che il capitale costante per operaio Z = Z(k) può essere espresso in forma non ricorsiva come:
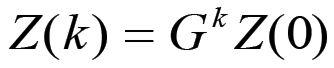 (2.35)
(2.35)Pertanto, utilizzando la (2.19), anche la funzione A = A(k) è facilmente esprimibile in forma non ricorsiva:
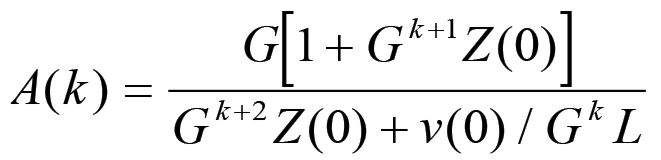 (2.36)
(2.36)La (2.36) mostra che, passando al limite, si ha:
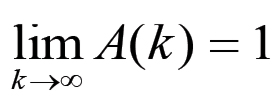 (2.37)
(2.37)indipendentemente dal valore di G se G > 1. Ciò significa che deve esistere un valore critico k = kc per cui A(k ) = G; in questo caso la (2.32) è verificata e la curva n = n(k) presenta un massimo. Inoltre, per k > kc otteniamo che δn(k) < 0, per cui la curva tende progressivamente a zero. Ciò avverrà tanto prima quanto maggiore sarà il valore di G, dunque quanto maggiore sarà il tasso di sviluppo delle forze produttive.
Non è difficile dimostrare, seguendo un procedimento analogo, l'esistenza di un massimo per la curva del plusvalore P = P(k). Anche in questo caso dovremo valutare la variazione della funzione passando da un ciclo all'altro. Ora, essendo per la (2.14) e la (2.33):
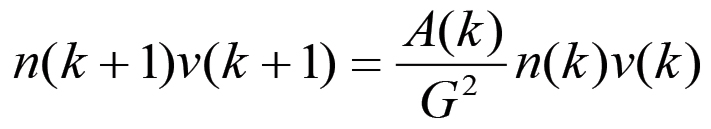
allora si ha che la variazione δP(k) della massa di plusvalore prodotta sarà data dall'espressione:
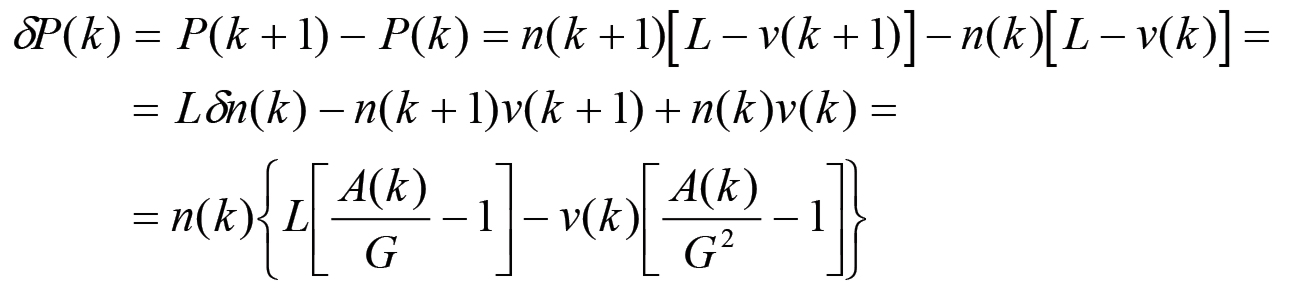 (2.38)
(2.38)dove abbiamo utilizzato la formula (2.32) per δn(k). Si noti che al punto critico k = kc la variazione δP(k) assume il valore:
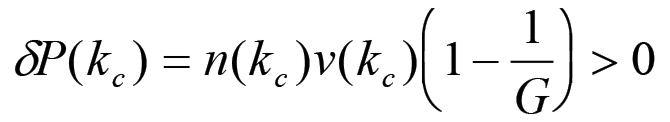
per cui l'eventuale punto di massimo deve essere successivo al punto di massimo che si riscontra nella curva della popolazione operaia. Essendo A = A(k) una funzione decrescente per valori elevati di k, si ha quindi che questo punto può esistere solo nell'intervallo di valori dell'indice k tali che A(k) < G, dunque per k > kc.
D'altra parte, osservando la (2.38) vediamo che l'esistenza di un massimo per la curva del plusvalore è condizionato dall'annullamento del fattore racchiuso in parentesi:

Inserendo in questa equazione la soluzione (2.34) per v(k ) e risolvendo in funzione di A(k) si ottiene quindi:
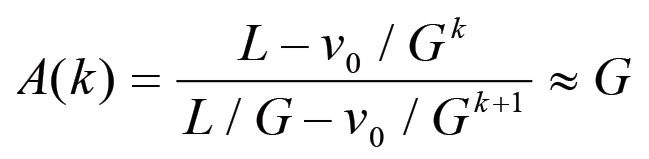
Pertanto, il punto di massimo per la curva P = P(k) coincide in pratica con il punto critico k = kc, dunque con il punto di massimo della curva n = n(k). Questa deduzione è confermata dall'andamento delle curve rappresentate nelle fig. 2.2 e 2.3.
Per quanto riguarda la curva di accumulazione, la presenza di un flesso è strettamente legata al massimo che si riscontra nella curva del plusvalore, in quanto è possibile dimostrare che la curva degli incrementi assoluti della funzione M = M(k) segue l'andamento della curva P = P(k). D'altra parte, è facile dimostrare che la funzione M = M(k) non è limitata superiormente da un asintoto orizzontale, per cui il suo andamento non è assimilabile a quello di una curva logistica. Infatti, usando la 2.36 possiamo risolvere la seconda delle eq. 2.14 e determinare in forma non ricorsiva la crescita della popolazione operaia. Si ha:
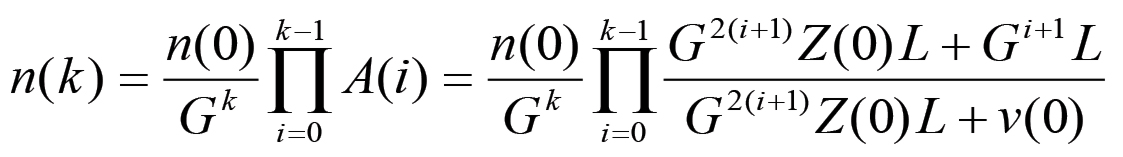 (2.39)
(2.39)Pertanto, in base alla 2.6 il capitale merce sarà dato da:
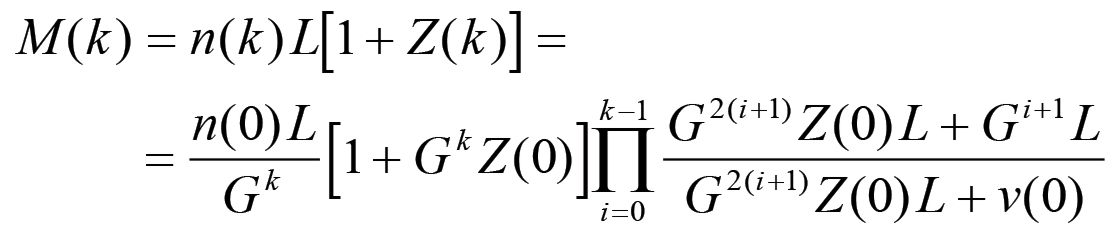 (2.40)
(2.40)Ora, per k→∞ si ha che il fattore che precede la produttoria tende a:
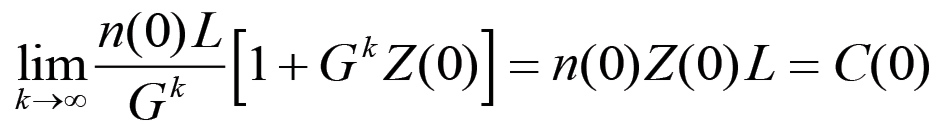
mentre il secondo termine risulta essere un prodotto di infiniti fattori tutti maggiori di uno, per cui tende all'infinito. In definitiva si ha che:
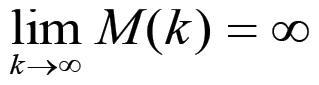
per cui la produzione complessiva non ha un limite superiore finito. D'altra parte la sua crescita procede, da un certo punto in avanti, per incrementi progressivamente decrescenti. Infatti, posto:
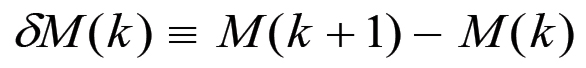
si ha che, per la (2.6) e la (2.14), gli incrementi assoluti della produzione saranno dati da:
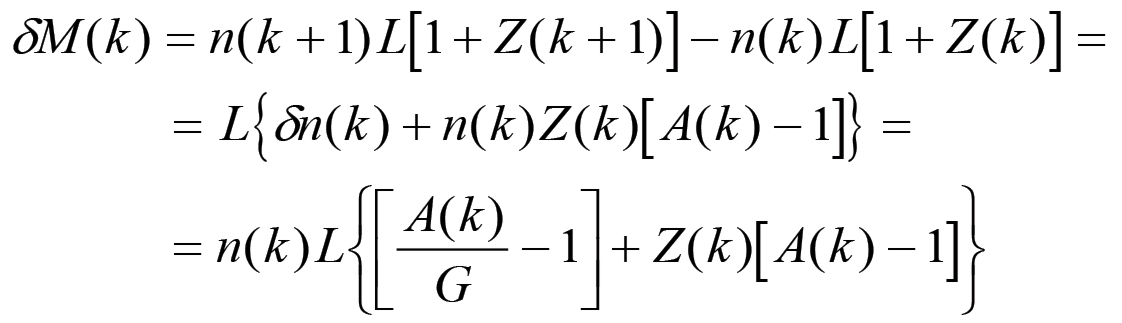
Effettuando ora il passaggio al limite per k→∞ otteniamo che mentre n(k) → 0, i due termini in parentesi tendono rispettivamente ai valori finiti:

Pertanto la curva degli incrementi δM(k) deve tendere a zero:
 (2.43)
(2.43)Ciò dimostra, almeno indirettamente, l'esistenza di un flesso nella curva di accumulazione, giacché la curva degli incrementi è crescente per valori piccoli del parametro temporale k.
Questo risultato è in perfetto accordo con il teorema fondamentale della concezione materialistica della Storia, il quale afferma l'esistenza di un punto a partire dal quale le forze produttive della società entrano in contraddizione con i rapporti di produzione esistenti; questi rapporti, da forme di sviluppo della forza produttiva del lavoro si convertono in catene che prima o poi verranno spezzate. Infatti, la diminuzione progressiva della massa del plusvalore e della popolazione operaia che si verificano una volta superato il punto critico k = kc, pur essendo processi a carattere tendenziale, determinano in modo ora latente ora esplosivo un progressivo deterioramento del sistema di rapporti di produzione. Già Marx, nel libro III del "Capitale", aveva espresso chiaramente la sostanza del problema:
"Uno sviluppo delle forze produttive che avesse come risultato di diminuire il numero assoluto degli operai, che permettesse in sostanza a tutta la nazione di compiere la produzione complessiva in un periodo minore di tempo, provocherebbe una rivoluzione perché ridurrebbe alla miseria la maggior parte della popolazione. Si manifesta qui nuovamente il limite specifico contro cui urta la produzione capitalistica e si dimostra chiaramente come essa non solo non rappresenti la forma assoluta per lo sviluppo delle forze produttive e della produzione della ricchezza, ma debba necessariamente, ad un certo punto, trovarsi in conflitto con questo sviluppo."
È questo in definitiva il quadro storico che segna il futuro del modo di produzione capitalistico.
2.3 - Analisi numerica dei dati economici
Nei paragrafi precedenti abbiamo focalizzato la nostra attenzione sulla meccanica del processo di accumulazione capitalistica allo scopo di mostrare come e perché il sistema di rapporti di produzione che ne costituisce il fondamento viene, ad un certo stadio del suo sviluppo, a trovarsi in contraddizione con la dinamica che sino a quel momento aveva provveduto a generare.
Vogliamo ora confrontare il movimento reale della produzione capitalistica, ed alcuni fatti storici collegati ad esso, con l'andamento generale previsto in base allo schema teorico dei paragrafi precedenti. È possibile innanzitutto confrontare le curve ottenute teoricamente con le serie statistiche relative alla produzione industriale annua su un arco di tempo abbastanza lungo e per un paese sufficientemente rappresentativo. Abbiamo scelto a questo proposito gli Stati Uniti, di cui sono disponibili i dati a partire dal 1860. In effetti, l'indice della produzione industriale rispecchia abbastanza bene l'andamento della curva dell'accumulazione per un dato paese, mentre è possibile dimostrare che il diagramma degli incrementi relativi sull'anno precedente è strettamente collegato all'andamento del tasso di accumulazione, dunque del saggio del profitto. Infine, è possibile utilizzare la curva degli incrementi assoluti per osservare l'andamento tendenziale della massa totale di plusvalore prodotta. Questi ultimi due grafici possono essere ottenuti facilmente a partire dai dati sulla produzione industriale.
D'altra parte, in uno studio di questo genere sorgono delle complicazioni, dovute per lo più alla estrema irregolarità delle curve degli incrementi relativi ed assoluti, anche quando l'andamento dell'indice della produzione è nettamente definito. Basta infatti una leggera oscillazione di questo diagramma attorno alla tendenza storica affinché le curve degli incrementi assumano un aspetto difficilmente interpretabile.
È facile comprendere che non è possibile regolarizzare direttamente, impiegando metodi numerici, un diagramma degli incrementi relativi o assoluti. Consideriamo un generico anno di partenza, ad esempio il 1860, e poniamo M(0) = 100.
Gli incrementi relativi saranno dati, per ogni anno successivo a quello di partenza, dalla funzione:
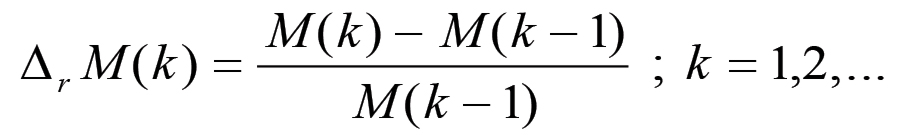 (2.44)
(2.44)Analogamente, gli incrementi assoluti saranno definiti dalla funzione:
 (2.45)
(2.45)Supponiamo ora che la funzione ΔrM(k) abbia, per k = 1,2,..., un andamento irregolare, ad esempio sia alternativamente +20%, -20%, +20%, etc. A prima vista può sembrare che il tasso medio di accumulazione sia zero, cioè che una regolarizzazione di ΔrM(k) porti ad una retta coincidente con l'asse delle ascisse. Questa conclusione sarebbe tuttavia sbagliata, in quanto ricavando M(k) dalla equazione (2.44) si ha invece: M(1) = 120, M(2) = 96, M(3) = 115.2, e così via. Ciò significa che una regolarizzazione della curva dei tassi non può essere effettuata trovando la migliore curva che passa attraverso i punti (come in effetti avviene per M(k)).
Nel caso in esame, una buona approssimazione si ottiene effettuando una media geometrica dei vari saggi d'incremento. Il tasso tendenziale medio non è quindi pari a zero ma sarà dato dalla retta ΔrM(k) = -2.02%. Ciò concorda con l'andamento reale della curva M = M(k), in quanto i dati forniti nell'esempio precedente mostrano una funzione che oscilla smorzandosi intorno all'esponenziale negativo con saggio pari al -2.02%. Ne concludiamo che non è possibile seguire i metodi standard di regolarizzazione nel caso dei tassi d'incremento. Tuttavia è possibile aggirare l'ostacolo regolarizzando la curva degli indici e ricavando i saggi d'incremento percentuale ed assoluto relativi alla curva regolare che si ottiene.
Per quanto riguarda la curva M = M(k), essa può essere facilmente regolarizzata utilizzando le tecniche standard dell'analisi numerica, ad esempio mediante un polinomio dei minimi quadrati di grado opportuno. Una volta isolata la tendenza generale è possibile infine procedere al calcolo degli incrementi relativi ed assoluti. In questo caso si otterranno curve regolari che potranno essere confrontate con quelle ottenute teoricamente per il saggio di accumulazione e la massa del plusvalore.
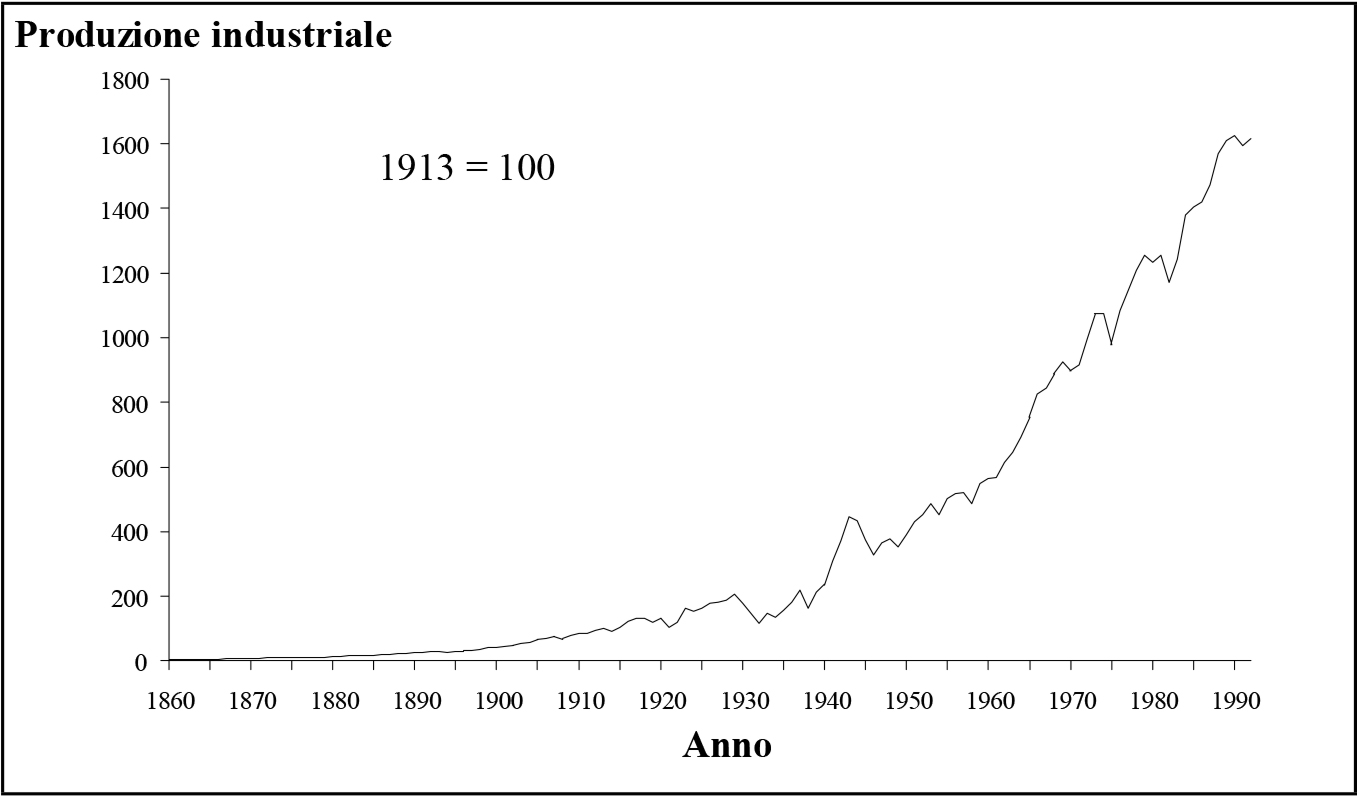 Fig. 2.5 - Indice della produzione industriale USA dal 1860 al 1992.
Fig. 2.5 - Indice della produzione industriale USA dal 1860 al 1992.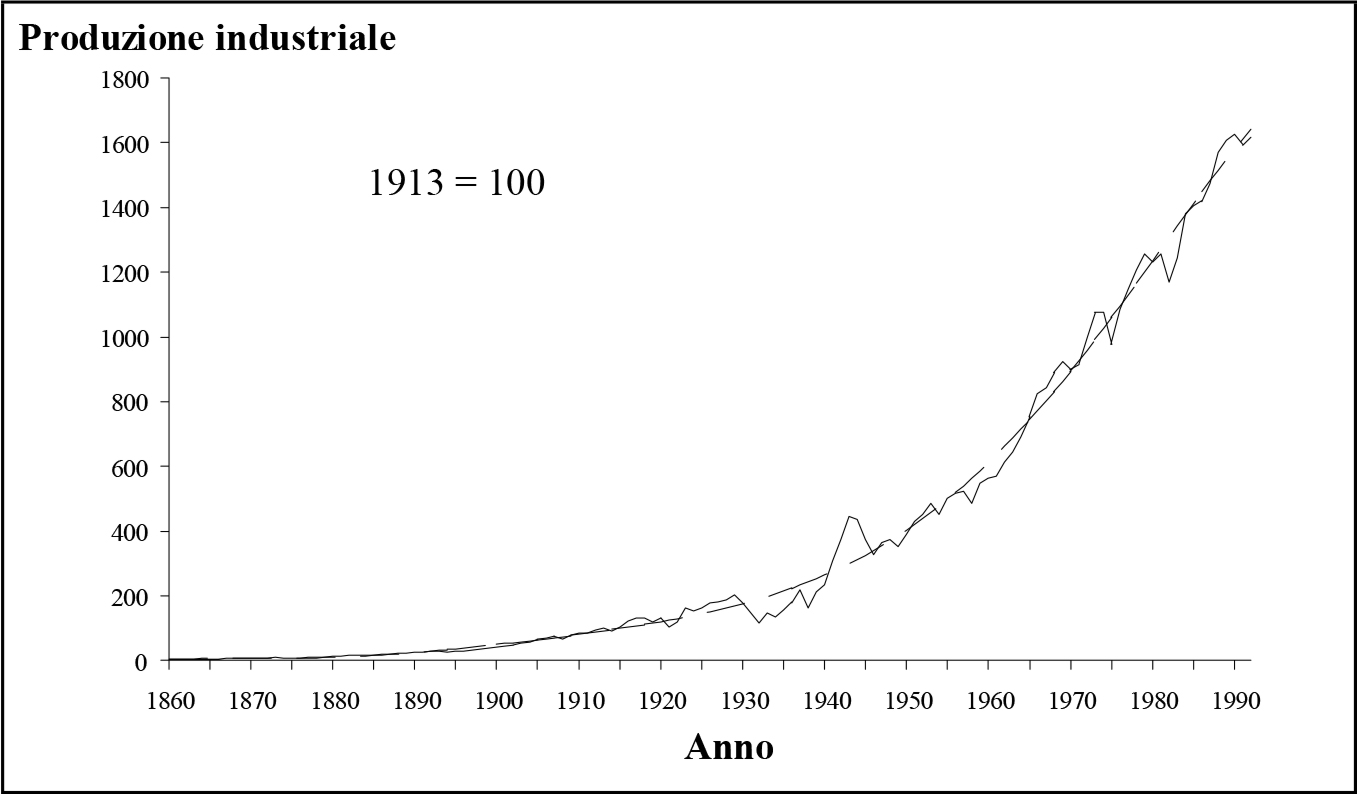 Fig. 2.6 - Produzione industriale USA e curva regolarizzata mediante un polinomio di VI grado.
Fig. 2.6 - Produzione industriale USA e curva regolarizzata mediante un polinomio di VI grado.I risultati dell'applicazione di questo metodo alla studio del processo di accumulazione negli Stati Uniti sono riportati nelle figure (2.5), (2.6), (2.7) e (2.8). In particolare, la fig. (2.5) è stata ottenuta in base ai dati relativi all'indice della produzione industriale comparsi su "il Programma Comunista" nel numero 16/1957 ed ai successivi aggiornamenti. Questi dati mostrano una successione di 26 cicli economici nell'arco di 130 anni, con una lunghezza media dei cicli pari a circa cinque anni, come mostra la tab. 2.1.
Le curve di fig. (2.6) mostrano invece la sovrapposizione tra il polinomio di regolarizzazione di grado sei e l'indice della produzione industriale. La curva regolarizzata presenta abbastanza chiaramente un flesso localizzato attorno al 1980. Questo fatto trova ovviamente un riscontro nel grafico regolarizzato degli incrementi assoluti (fig. 2.7), il quale presenta un massimo nello stesso periodo. Ciò da un lato conferma la previsione teorica relativa all'esistenza di un massimo per la curva del plusvalore, dall'altra ci porta a concludere che il modo di produzione capitalistico ha ormai raggiunto un punto di catastrofe per l'evoluzione dei rapporti di classe. D'altra parte, è ben visibile la repentina impennata delle tensioni sociali su scala internazionale a partire dalla crisi iraniana del 1979. Questa brusca transizione è tuttora in corso, come mostrano i recenti avvenimenti in Iraq, Jugoslavia e Somalia.
I dati riportati nella fig. 2.8 mostrano infine la tendenza generale del tasso di accumulazione. Anche in questo caso si ha una buona concordanza con i risultati del modello teorico. Pertanto, possiamo affermare che l'elaborazione dei dati relativi alla produzione industriale conferma in modo soddisfacente le previsioni formulate teoricamente nei paragrafi precedenti.
Una conferma definitiva richiede comunque lo studio della curva della popolazione operaia. La fig. 2.9 mostra l'andamento della popolazione operaia industriale negli Stati Uniti dal 1900 al 1990 e la relativa regolarizzazione numerica, effettuata mediante un polinomio di IV grado. Si osserva qui un massimo localizzato alla fine degli anni '70, corrispondente al punto critico k = kc ricavato nel paragrafo precedente. Il leggero anticipo rispetto al massimo della curva P = P(k) trova dunque una conferma sperimentale.
In definitiva, questa conferma del modello teorico, in tutti i suoi aspetti, ci consente di stabilire che la tendenza generale del modo di produzione capitalistico, dunque la tendenza che si afferma su lunghi periodi di tempo, è quella stabilita dall'aumento storico della forza produttiva del lavoro sociale. Ne segue che i fenomeni su piccola scala relativi alla dinamica interna dei cicli economici, che verranno comunque presi in considerazione nei capitoli successivi, possono solo determinare un'oscillazione più o meno ampia attorno alla tendenza generale descritta in precedenza.
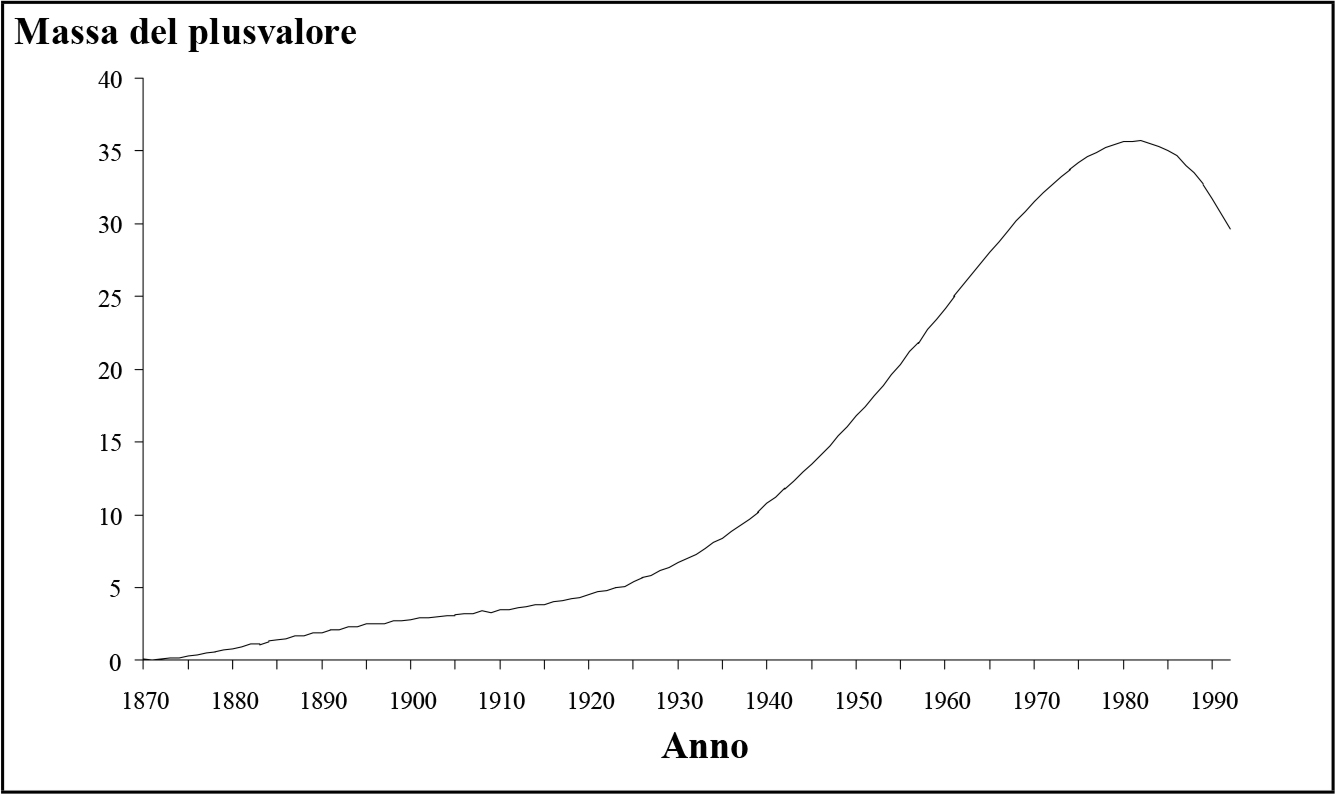 Fig. 2.7 - Incrementi assoluti associati alla curva regolarizzata della
produzione industriale USA.
Fig. 2.7 - Incrementi assoluti associati alla curva regolarizzata della
produzione industriale USA.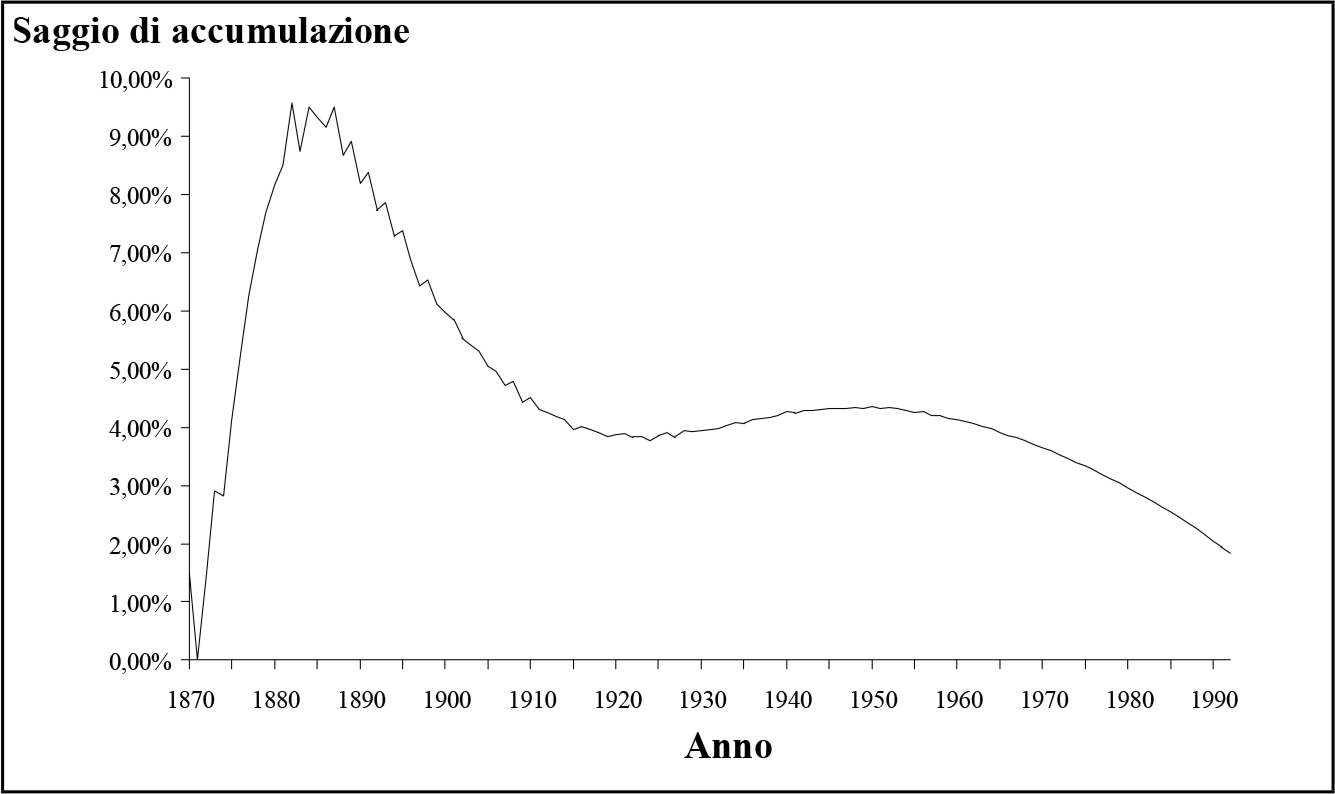 Fig. 2.8 - Saggio tendenziale di accumulazione associato alla curva regolarizzata della produzione industriale USA.
Fig. 2.8 - Saggio tendenziale di accumulazione associato alla curva regolarizzata della produzione industriale USA.| Periodo | Contesto | Ciclo | Durata |
|---|---|---|---|
| 1862-1863 1864 |
Crisi Espansione |
1 |
3 |
| 1865-1866 1867 |
Crisi Espansione |
2 |
3 |
| 1868-1870 1871-1873 |
Crisi Espansione |
3 |
6 |
| 1874-1876 1877 |
Crisi Espansione |
4 |
4 |
| 1878 1879-1883 |
Crisi Espansione |
5 |
6 |
| 1884-1885 1886-1888 |
Crisi Espansione |
6 |
5 |
| 1889 1890-1892 |
Crisi Espansione |
7 |
4 |
| 1893-1894 1895 |
Crisi Espansione |
8 |
3 |
| 1896 1897-1907 |
Crisi Espansione |
9 |
12 |
| 1908 1909-1910 |
Crisi Espansione |
10 |
3 |
Tab. 2.1 - I cicli economici di breve periodo dell'industria USA (1860 - 1990)
| Periodo | Contesto | Ciclo | Durata |
|---|---|---|---|
| 1911 1912-1913 |
Crisi Espansione |
11 |
3 |
| 1914 1915-1917 |
Crisi Espansione |
12 |
4 |
| 1918-1919 1920 |
Crisi Espansione |
13 |
3 |
| 1921 1922-1923 |
Crisi Espansione |
14 |
3 |
| 1924 1925-1929 |
Crisi Espansione |
15 |
6 |
| 1930-1932 1933 |
Crisi Espansione |
16 |
4 |
| 1934 1935-1937 |
Crisi Espansione |
17 |
4 |
| 1938 1939-1943 |
Crisi Espansione |
18 |
6 |
| 1944-1946 1947-1948 |
Crisi Espansione |
19 |
5 |
| 1949 1950-1953 |
Crisi Espansione |
20 |
5 |
Tab. 2.1 - I cicli economici di breve periodo dell'industria USA (1860 - 1990)
| Periodo | Contesto | Ciclo | Durata |
|---|---|---|---|
| 1954 1955-1957 |
Crisi Espansione |
21 |
4 |
| 1958 1959-1969 |
Crisi Espansione |
22 |
12 |
| 1970 1971-1973 |
Crisi Espansione |
23 |
4 |
| 1974-1975 1976-1979 |
Crisi Espansione |
24 |
6 |
| 1980 1981 |
Crisi Espansione |
25 |
2 |
| 1982 1983-1990 |
Crisi Espansione |
26 |
9 |
Tab. 2.1 - I cicli economici di breve periodo dell'industria USA (1860 - 1990)
In effetti, alla scala storicamente microscopica dei 3,5 o anche 10 anni assumono rilevanza fenomeni come il credito, la rendita, il movimento dei prezzi, la circolazione del denaro, etc., mentre le leggi fondamentali, a grande scala, del modo di produzione capitalistico agiscono a livello latente, manifestandosi solo periodicamente con le crisi.
Questa è una regola generale: quanto più piccola è la scala di osservazione tanto più grande è la perturbazione che un'infinità di fenomeni transitori causa all'andamento generale di un processo (fisico, biologico, storico, etc.); su una scala più grande, invece, gli effetti combinati dei vari fattori secondari si compensano a vicenda e quella che rimane è una tendenza generale suscettibile di descrizione a livello teorico per mezzo di un processo di astrazione. Possiamo inoltre notare che per la maggioranza di questi fenomeni secondari è addirittura impossibile una descrizione esatta della loro influenza sul processo principale; ma dove non c'è regolarità non c'è scienza, per cui il processo di astrazione rimane un metodo irrinunciabile per ogni teoria scientifica.
In ogni caso, i grafici riportati mostrano chiaramente la necessità storica della catastrofe finale del modo di produzione borghese, così come prefigurata da Marx; non conosciamo i modi ed i tempi che caratterizzeranno l'ultimo atto della preistoria umana, ma una cosa è certa: non sarà una crisi quella che imporrà al proletariato di portare l'assalto al cielo ma l'impossibilità di risolvere le contraddizioni che l'hanno generata nell'ambito dei rapporti di produzione borghesi.
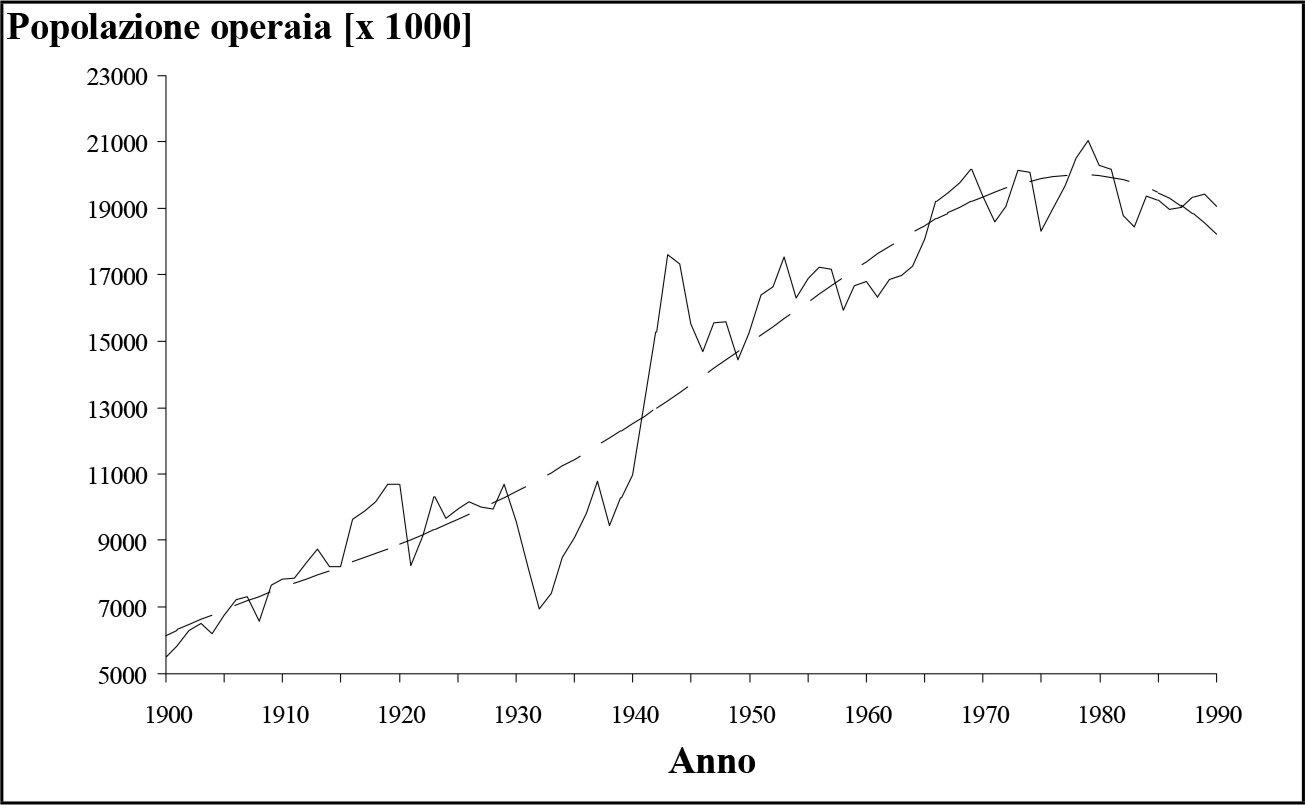 Fig. 2.9 - Popolazione operaia industriale USA e regolarizzazione della curva mediante un polinomio di IV grado.
Fig. 2.9 - Popolazione operaia industriale USA e regolarizzazione della curva mediante un polinomio di IV grado.Quali possono essere le conseguenze per la società capitalistica derivanti dal dispiegamento della contraddizione tra forze produttive e rapporti di produzione? In altri termini, cosa implica la presenza di un flesso nella curva di accumulazione, cosa è cambiato a partire dalla fine degli anni settanta? La risposta a queste domande richiede delle considerazioni aggiuntive e non può essere fornita nell'ambito di un'analisi astratta dell'evoluzione delle variabili economiche.
Il risultato principale a cui siamo pervenuti consiste nella dimostrazione matematica dell'esistenza di un punto di massimo nelle curve del plusvalore e della popolazione operaia. Inoltre, lo studio dei dati disponibili suggerisce che questo punto sia stato effettivamente raggiunto alla fine degli anni settanta. Se si accetta questo risultato bisogna anche accettare la sua logica conseguenza, il fatto cioè che in queste condizioni il modo di produzione borghese entra in una fase in cui la miseria della maggior parte della popolazione mondiale aumenta progressivamente ed in modo inarrestabile, giacché ad ogni ciclo economico diminuisce la popolazione in grado di essere assorbita nel processo produttivo. Svanisce così il mito borghese della fabbrica automatica e della società del benessere, in quanto il mondo non potrà che assistere alla progressiva intensificazione della lotta di classe, dapprima come lotta alle forme delle contraddizioni sociali, in seguito, quando le forme si muteranno nella sostanza, come lotta alla società borghese in quanto tale. E sarà rivoluzione comunista.
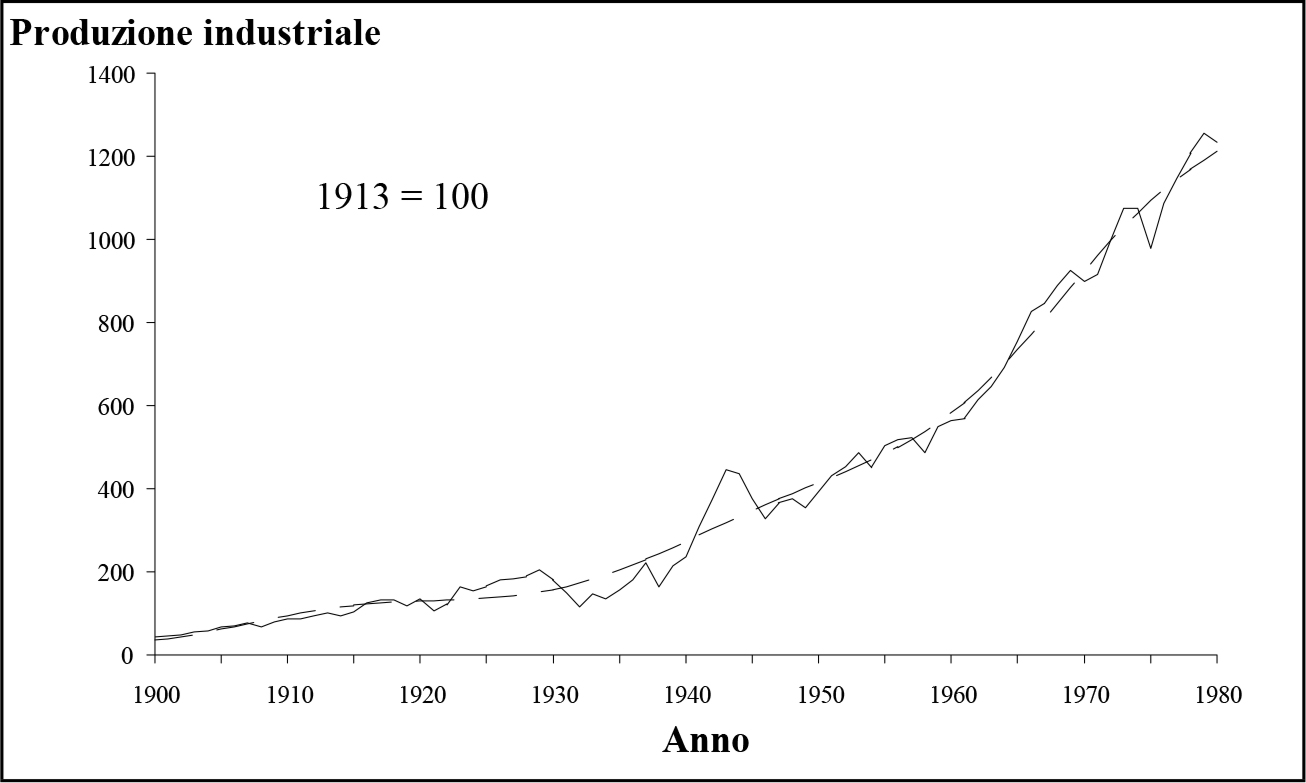 Fig. 2.10 - Indice della produzione industriale USA dal 1900 al 1980 e regolarizzazione al XIII grado.
Fig. 2.10 - Indice della produzione industriale USA dal 1900 al 1980 e regolarizzazione al XIII grado.Detto ciò, viene automaticamente a cadere una possibile ed erronea interpretazione dei risultati precedenti, consistente nel dire che il capitalismo entra nella sua "fase discendente". Il marxismo non si occupa di astratte grandezze matematiche che evolvono secondo leggi prestabilite; piuttosto, il nostro compito è principalmente quello di analizzare i riflessi sovrastrutturali dei fenomeni economici, ovvero i movimenti sociali a cui danno luogo, con tutto l'insieme di forme ideologiche che consentono alle classi di concepire lo scontro in atto: sarà essenzialmente una chiara visione dei possibili sviluppi della lotta di classe che abiliterà il Partito del proletariato a trasformarsi ad un certo punto in fattore storico.
La precedente analisi numerica dei dati è stata effettuata utilizzando un polinomio di regolarizzazione di grado sei, poco suscettibile alle deviazioni su scala intermedia dalla tendenza generale. Effettuando invece una regolarizzazione mediante un polinomio di grado 13 si ottengono le curve mostrate nelle figure (2.10), (2.11) e (2.12). La fig. (2.10) è analoga alla (2.6) e riporta la sovrapposizione del polinomio di regolarizzazione di grado 13 alla curva degli indici della produzione industriale. Questo diagramma mostra chiaramente un adeguamento maggiore della curva regolarizzata alla curva effettiva. Osserviamo ora la fig. (2.11), nella quale sono rappresentati gli incrementi assoluti regolarizzati che si ottengono dal polinomio di grado 13.
 Fig. 2.11 - Incrementi assoluti associati alla curva regolarizzata della produzione industriale USA (XIII grado).
Fig. 2.11 - Incrementi assoluti associati alla curva regolarizzata della produzione industriale USA (XIII grado).Se interpretiamo questo grafico come un indice tendenziale della produzione di plusvalore dal 1900 al 1980, osserviamo tre grandi cicli che ripropongono su scala intermedia un andamento analogo a quello previsto per l'intero corso del capitalismo. Nell'ambito di ciascuno di questi tre cicli di secondo ordine, la curva del plusvalore presenta infatti un massimo corrispondente ad un flesso nella curva di accumulazione.
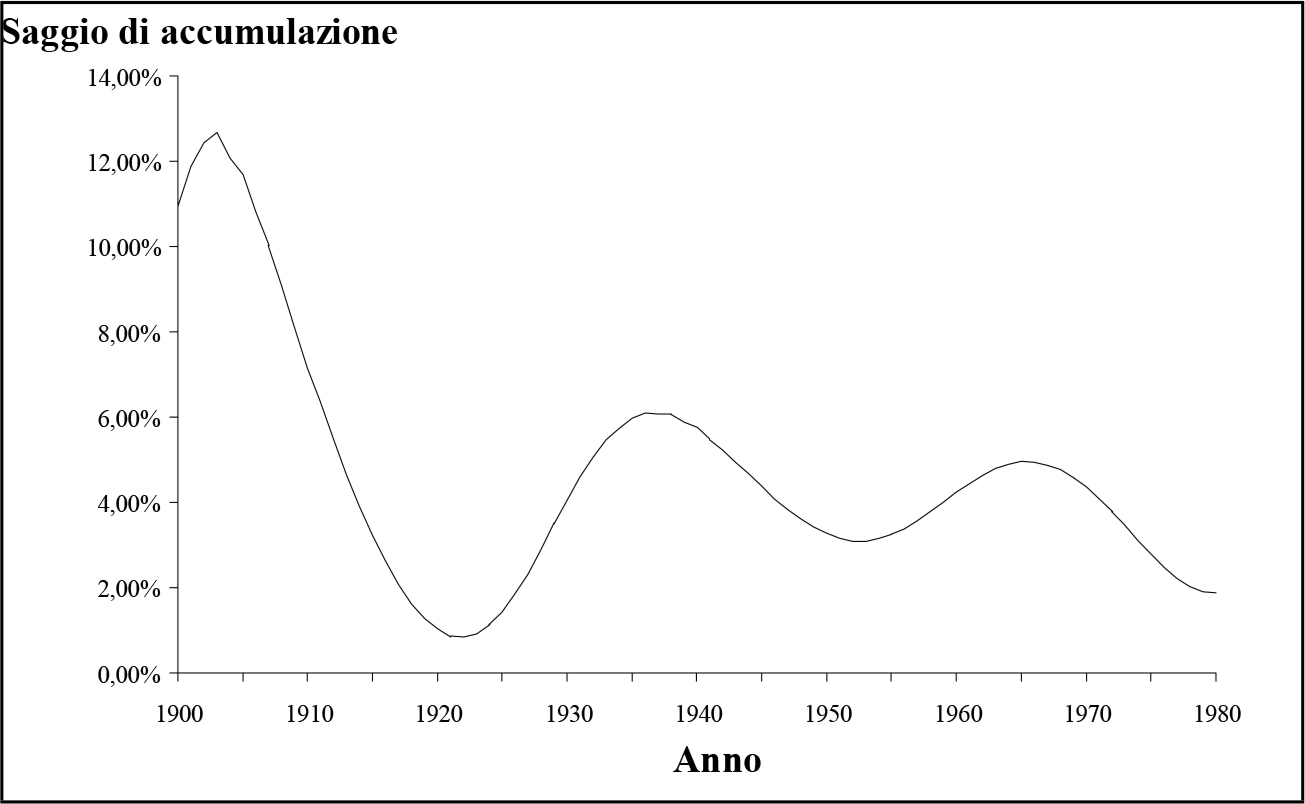 Fig. 2.12 - Saggio tendenziale di accumulazione associato alla curva regolarizzata della produzione industriale USA (XIII grado).
Fig. 2.12 - Saggio tendenziale di accumulazione associato alla curva regolarizzata della produzione industriale USA (XIII grado).L'interpretazione di questo fenomeno, come vedremo tra breve, ci consentirà di effettuare delle considerazioni tutt'altro che secondarie. Essa d'altra parte non mette assolutamente in discussione le conclusioni raggiunte in base all'analisi con polinomi di VI grado, in quanto la curva che si ottiene al XIII grado non fa altro che oscillare attorno a quella di grado inferiore.
Notiamo innanzitutto che i massimi di fig. (2.11) sono localizzati attorno al 1907-1908, al 1942 ed al 1969, mentre i minimi, che segnano l'inizio di un nuovo ciclo su scala intermedia (o ciclo di secondo ordine), sono localizzati rispettivamente attorno al 1921-1922, al 1951 ed al 1979. Questi tre cicli durano rispettivamente 30, 34 e 27 anni e comprendono a loro volta 7, 6 e 4 cicli brevi di espansione-crisi, ovvero cicli di terzo ordine. La fig. (2.12), infine, mostra nel periodo 1900-1980 l'andamento del tasso d'incremento relativo della produzione industriale, regolarizzato mediante il polinomio di grado 13. Questa curva è collegata, come sappiamo, al tasso di accumulazione e quindi al saggio medio del profitto. Anche in questo caso possiamo osservare, oltre alla diminuzione storica, la presenza di tre cicli intermedi di secondo ordine.
La spiegazione di questa ciclicità intermedia richiede l'anticipazione di alcuni concetti e non può essere data nel quadro generale della teoria sviluppata nei paragrafi precedenti. Osserviamo la fig. (2.13), la quale mostra l'andamento dei prezzi delle materie prime nell'arco di tempo compreso tra il 1860 ed il 1980. In questa curva si individuano chiaramente tre grandi cicli, caratterizzati da tre picchi nei prezzi, precisamente nel 1920, nel 1951 e nel 1980. Ciascuno di questi picchi è determinato da una fase di rapida crescita dei prezzi delle materie prime seguito da un crollo brusco. Vedremo nei prossimi capitoli che questo tipo di andamento è una caratteristica del processo di accumulazione nelle sfere soggette al meccanismo della rendita, in particolare dunque nell'agricoltura e nell'industria mineraria. Ed è proprio a questi "cicli della rendita" che va attribuita la ciclicità di secondo ordine della curva di accumulazione. Nei periodi in cui i prezzi delle materie prime aumentano, la forza produttiva del lavoro diminuisce in queste sfere di produzione e si ha la progressiva formazione di rendita differenziale. Ciò determina un effetto diverso sulle variabili globali F e Z. Per quanto riguarda la grandezza F, essa aumenterà meno rapidamente di quanto farebbe in assenza di meccanismi legati alla rendita.
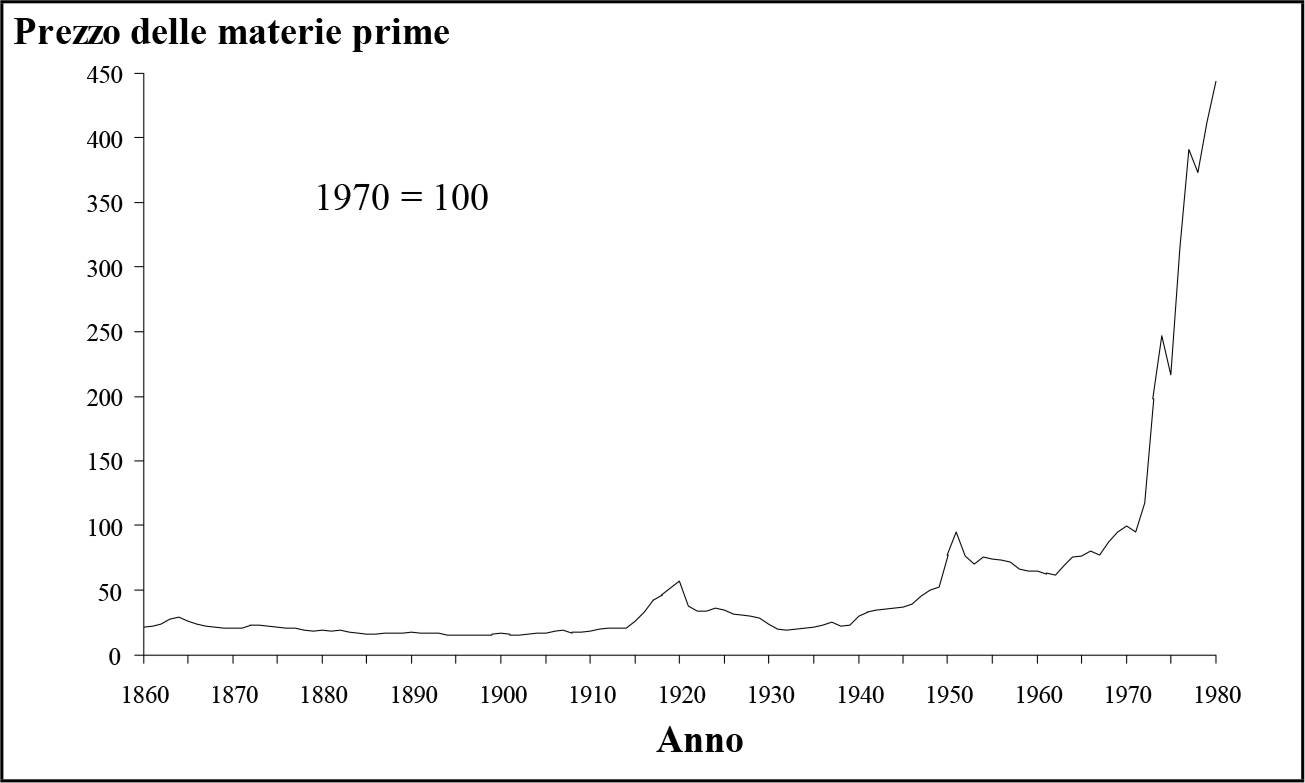 Fig. 2.13 - Indice dei prezzi delle materie prime sul mercato mondiale.
Fig. 2.13 - Indice dei prezzi delle materie prime sul mercato mondiale.Il processo di accumulazione determina infatti la messa a coltura di terreni sempre meno fertili e lo sfruttamento di miniere sempre meno produttive, in quanto i settori industriali richiedono una quantità progressivamente maggiore di materie prime e sono disposti a pagare prezzi sempre più alti. Ciò costituisce chiaramente un limite per la crescita della forza produttiva del lavoro sociale, la quale per un certo periodo di tempo può aumentare solo grazie al processo di automazione nei settori industriali. Per quanto riguarda invece la variabile Z, essa aumenta non solo in seguito al processo di sostituzione di macchine ad uomini, ma anche a causa del carico aggiuntivo che si determina sul capitale costante impiegato dalla società quando i prezzi delle materie prime aumentano. Pertanto, contrariamente alla nostra assunzione originaria (vedi par. 1.6) le grandezze F e Z hanno una dinamica diversa e la curva di accumulazione genera un flesso secondario, corrispondente ad un massimo relativo nel diagramma del plusvalore. Ad un certo punto, però, il meccanismo di accumulazione portato avanti mediante la progressiva formazione di rendita differenziale si inceppa, in quanto le risorse naturali, ad un determinato grado di sviluppo delle tecnologie agricole e minerarie, hanno un limite assoluto nell'estensione del territorio e delle miniere, per cui la stessa produzione complessiva non può superare un certo limite se le forze produttive restano invariate. Questo fatto determina un improvviso crollo dei prezzi ed apre la strada ad un nuovo sviluppo della forza produttiva del lavoro nelle campagne. Infatti, il grafico di fig. (2.13) mostra che subito dopo il crollo, i prezzi delle materie prime subiscono una graduale diminuzione. Questo fenomeno si traduce ora in una inversione di tendenza per quanto riguarda le variabili F e Z, in quanto la prima subirà un forte aumento, la seconda una brusca diminuzione. Parallelamente, la curva tendenziale del plusvalore presenterà un minimo relativo seguito da una nuova ripresa, proprio come risulta dalla fig. (2.11). Ciò segna l'avvio di un nuovo ciclo di secondo ordine e il processo si ripete. Questo argomento verrà comunque approfondito nel corso dei capitoli successivi. Notiamo per ora che la tendenza che si osserva nella parte finale della curva di fig. 2.13 risulta amplificata dal fenomeno inflazionistico di questo ultimo mezzo secolo. In effetti, una curva del valore reale delle materie prime mostrerebbe una ciclicità di secondo ordine che si sovrappone ad una tendenza generalmente discendente, come avremo modo di dimostrare nel capitolo IV.

Dinamica dei processi storici Volume I
Teoria dell'accumulazione
Quaderni di n+1.
Una formalizzazione spinta del sistema di riferimento marxista. In questo volume gli schemi di Marx vengono affiancati da una ulteriore dimostrazione poggiante su potenti strumenti matematici che confermano il carattere transitorio del capitalismo.

 n+1
n+1