Capitolo I. La parabola del plusvalore
ELENCO DEI SIMBOLI
M - Capitale merce.
q - Produzione, in massa, di un ramo industriale, espressa in unità fisiche.
u - Valore o prezzo unitario di un ramo d'industria oppure valore globale di riferimento.
uap - unità adimensionale di prodotto.
Q - Produzione, in massa, di un ramo industriale, espressa in unità adimensionali.
β- Parametri di un sistema di riferimento; matrice di accoppiamento; frazione della produzione industriale che viene reintrodotta in questa stessa sezione.
C - Capitale costante.
K - Rapporto tra il capitale merce ed il tempo di lavoro aggiunto.
ϑ - Rapporto tra il capitale costante ed il capitale merce.
W - Valore prodotto ex-novo.
P - Massa del plusvalore.
V - Capitale variabile.
Ω - Composizione organica del capitale.
S - Saggio del plusvalore.
Ω - Rapporto tra il valore prodotto ex-novo ed il capitale costante.
D - Capitale anticipato.
τ - Saggio del profitto.
γ - Rapporto tra massa del plusvalore e capitale merce, ovvero frazione del capitale merce che si trasforma in plusvalore; indice di fertilità dei terreni.
ε - Frazione del plusvalore consumata non produttivamente dai capitalisti.
σ - Indice di sovrapproduzione; massa di valori d'uso (in uap) equivalenti al salario.
α - Saggio di accumulazione; saggio di aumento del salario.
QW - Frazione della produzione complessiva equivalente al valore prodotto ex-novo (in uap).
QC - Frazione della produzione complessiva equivalente al capitale costante (in uap).
n - Popolazione operaia occupata.
L - Valore prodotto ex-novo da un singolo operaio annualmente, ovvero durata della giornata lavorativa per il numero di giornate in un anno.
F - Forza produttiva del lavoro.
Z - Rapporto tra il capitale costante ed il valore prodotto ex novo, ovvero capitale costante trasferito per operaio nell'unità di tempo.
G - Fattore di aumento della forza produttiva del lavoro.
uc - Capitale costante contenuto in una unità di prodotto.
uw - Valore prodotto ex novo contenuto in una unità di prodotto.
v - Valore della forza lavoro.
χ - Indice inverso della scala della produzione.
π - Perdite subite da una sezione della riproduzione nel corso di una crisi.
η - Velocità di circolazione del denaro.
A - Fattore di espansione della scala della produzione.
R' - Rendita assoluta.
ρ - Saggio della rendita assoluta.
μ - Densità di capitale, ovvero capitale investito per unità di superficie.
φ - Grado di fertilità dei terreni.
R" - Rendita differenziale.
R - Rendita totale.
ι - Saggio d'interesse.
Γ - Debito del settore industriale.
H - Fattore di aumento del capitale costante per operaio.
QV - Frazione della produzione complessiva equivalente al capitale variabile (in uap).
1.1 - Sistemi di riferimento
Il capitale merce complessivo prodotto nel corso di un generico anno di riproduzione materiale è costituito dall'unione di molti capitali particolari, ciascuno dei quali è il risultato del processo lavorativo e di valorizzazione che si attuano nell'ambito di una particolare sfera produttiva. Detto N il numero di rami d'industria che compongono il sistema di riproduzione, la produzione totale annua della società sarà dunque costituita da N tipi di merci prodotte nelle quantità q1,q2,...,qN ai prezzi unitari u1,u2,...,uN. Se Mi è il valore della produzione relativa alla sfera i-esima, allora si ha che:
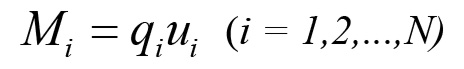 (1.1)
(1.1)
In questa formula le quantità qi sono espresse in unità metriche distinte, che in generale dipendono dalle caratteristiche fisiche dei prodotti (ad es. tonnellate, metri, etc.), oppure in unità adimensionali nel caso di altri prodotti (ad es. le automobili). Il prezzo unitario ui può invece essere l'espressione di un valore unitario, ovvero del tempo di lavoro socialmente necessario alla fabbricazione di un'unità di prodotto, oppure di un prezzo di produzione determinato dal saggio medio del profitto e dalla composizione organica del capitale che opera in quella determinata sfera di produzione. Quest'ultima determinazione si afferma di norma nei rami industriali non soggetti al meccanismo della rendita. Supponiamo ora che la giornata lavorativa media abbia una durata oraria prefissata. In questo caso è possibile assumere come unità di tempo di lavoro una giornata lavorativa semplice (in breve 1 gl) ed esprimere il prezzo unitario in termini di giornate lavorative per unità di produzione (ad es. gl/ton), eliminando così i problemi connessi alla rappresentazione del valore in termini di prezzo, cioè in termini di denaro. Infatti il denaro stesso, in quanto merce, è soggetto a variazioni di valore. Questo fatto determina l'impossibilità di studiare gli effetti dei cambiamenti della forza produttiva del lavoro sociale osservando le variazioni di prezzo. Queste esprimono, in ultima analisi, variazioni relative della forza produttiva del lavoro tra le diverse sfere di produzione. Vogliamo ora introdurre una misura della produzione totale annua, cioè una grandezza che esprima la quantità totale di merci prodotte nel corso di un ciclo di riproduzione. A tal fine è necessario ridurre le grandezze q1,q2,...,qN, che sono per ora espresse in unità differenti, ad unità standard adimensionali che rappresentano, per ogni tipo di merce, una grandezza di valore prefissata. Questa operazione può essere effettuata fissando una quantità arbitraria u di valore, corrispondente ad un determinato tempo di lavoro (ad esempio ponendo u = 1 giorno di lavoro semplice), e definendo un'unita' adimensionale di prodotto (in breve 1 uap) come la quantità di valori d'uso di un certo tipo necessaria a formare un valore pari ad u (ad esempio 100 kg di pane, 15 kg di carne, 20m di stoffa, etc.). Vediamo ora in che modo è possibile esprimere le quantità q1,q2,...,qN per mezzo di un nuovo insieme di grandezze adimensionali Q1,Q2,...,QN, ciascuna delle quali rappresenta, in unità adimensionali (uap), la produzione della rispettiva sfera. Consideriamo le quantità β1, β2,...,βN di ciascun valore d'uso necessarie a formare 1 uap. Si ha chiaramente che:
 (1.2)
(1.2)
Ad esempio, se u = 100 giorni di lavoro ed il valore di una tonnellata di zinco è pari a 3.3 giornate lavorative, allora β = 30 ton, cioè occorrono 30 tonnellate di zinco per formare 1 uap di questa merce. Assegnata la grandezza u, l'insieme {β1,β2,...,βN} definisce un sistema di riferimento per mezzo del quale possiamo rappresentare la produzione complessiva della società. Naturalmente, una scelta diversa per u determinerà un diverso insieme di parametri {β'1,β'2,...,β'N}. Una volta determinato un sistema iniziale mediante una grandezza di riferimento u, è possibile passare ad un altro sistema, con diverso valore di riferimento u', per mezzo di trasformazioni del tipo:
 (1.3)
(1.3)
dove β'i = u'/ui (i = 1,2,...,N). Chiameremo lineare ogni trasformazione di questo genere. Supponiamo ora che sia stato assegnato un sistema {β1}; le quantità q1,q2,...,qN possono essere trasformate nelle quantità adimensionali Q1,Q2,...,QN ponendo:
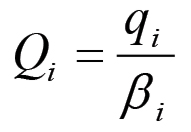 (1.4)
(1.4)
Sia ad esempio u = 100 giorni di lavoro. Se si ha una scomposizione della produzione sociale del tipo mostrato nella tabella 1.1:
| i | Merce | q | u |
|---|---|---|---|
| 1 | Caffè | 4756000 ton | 18.4 gl/ton |
| 2 | Alluminio | 14221000 ton | 7.5 gl/ton |
| 3 | Nickel | 750000 ton | 29.9 gl/ton |
| 4 | Automobili | 20000000 | 50 gl |
| ... | ... | ... | ... |
Tab. 1.1: Esempio di composizione del prodotto totale annuo
allora, per la (1.2) e la (1.4), si avrà che i parametri βi e le grandezze adimensionali Qi assumeranno i valori riportati nella tabella 1.2:
| i | β | Q [uap] |
|---|---|---|
| 1 | 5.4 ton | 880740.7 |
| 2 | 13.3 ton | 1069248.1 |
| 3 | 3.3 | 227272.7 |
| 4 | 2.0 | 10000000.0 |
| ... | ... | ... |
Tab. 1.2: Parametri e quantità adimensionali Q
Siamo ora in grado di esprimere tutti i capitali merce Mi, relativi ad ogni sfera di produzione, come prodotto tra una quantità adimensionale, che esprime la quantità di prodotti fabbricati, ed un valore generale di riferimento u valido per tutti i tipi di merce. Infatti, sostituendo nella (1.1) le espressioni (1.2) e (1.4) si ha:
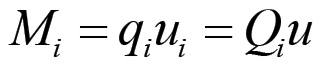 (1.5)
(1.5)
Il capitale merce complessivo della società sarà quindi dato da:
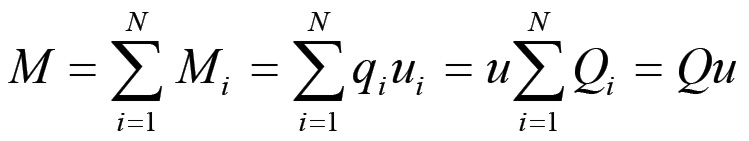 (1.6)
(1.6)
dove abbiamo posto Q = Q1+Q2+...+QN . Consideriamo ora una variazione generalizzata ed uniforme dei valori individuali u:
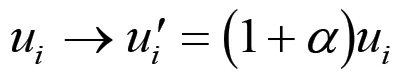 (1.7)
(1.7)
Nel sistema di riferimento {βi}, e supponendo costanti le qi, si ha che le Qi per la (1.4) resteranno costanti (Q'i = Qi), mentre u subirà una variazione data da:
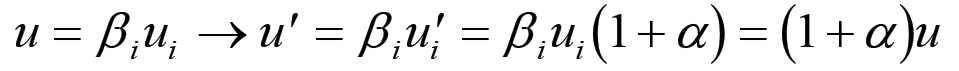 (1.8)
(1.8)
Pertanto si avrà che:
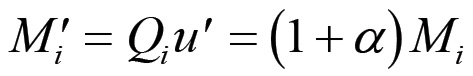 (1.9)
(1.9)
 (1.10)
(1.10)
Questo è un risultato significativo, in quanto conferma la possibilità di utilizzare delle quantità adimensionali per esprimere l'estensione della scala della produzione. Infatti, una rivoluzione di valore, cioè un cambiamento generalizzato dei valori individuali causato da una variazione della forza produttiva del lavoro sociale, mentre modifica il valore di riferimento u e la grandezza del capitale sociale, lascia invariate le quantità adimensionali Qi se la produzione di ogni singola sfera resta immutata, per cui la stessa produzione complessiva Q, espressa in uap, resta costante. Questo risultato non sarebbe valido nel caso di variazioni isolate nei valori individuali, oppure se questi variassero in misura diversa, per cui la rappresentazione del prodotto complessivo per mezzo di unità adimensionali può essere convenientemente adottata solo per studiare il movimento complessivo della produzione sociale, trascurando ogni eventuale variazione relativa tra le sue parti, dunque eventuali variazioni individuali localizzate della forza produttiva del lavoro e dei prezzi.
Notiamo inoltre che se effettuiamo una trasformazione lineare del tipo (1.3), questa lascia invarianti Mi ed M ma modifica le grandezze Qi. Infatti, posto:
 (1.11)
(1.11)
si ha che:
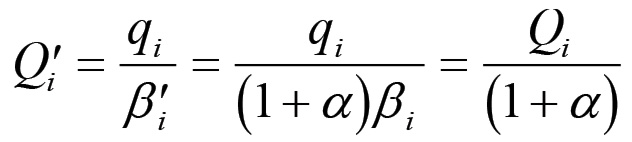 (1.12)
(1.12)
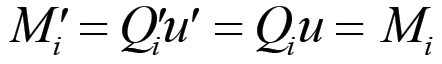 (1.13)
(1.13)
Ciò da un lato conferma l'arbitrarietà nella scelta iniziale di u, in quanto Mi è indipendente per la (1.13) dalla scelta del sistema di riferimento, dall'altra implica che la grandezza assoluta delle Qi dipende da questa scelta, per cui ciò che effettivamente conta ai fini dell'analisi del processo di accumulazione sono le variazioni di queste grandezze, che sono proporzionali alle variazioni delle quantità effettive ed esprimono mutamenti nella scala della produzione. In definitiva, le grandezze Q ed u esprimono in modo opportuno l'indice della produzione complessiva e l'indice del valore unitario dei prodotti quando si studia il movimento generale della produzione capitalistica, ovvero l'estensione della scala della produzione a seguito del processo di accumulazione e le variazioni della forza produttiva del lavoro sociale nell'ambito di rivoluzioni decisive delle tecniche di produzione.
1.2 - Il valore come osservabile
I risultati precedenti sono stati ottenuti in base al presupposto che fossero noti i valori individuali ui delle merci prodotte annualmente nei diversi rami d'industria, in altri termini che queste grandezze fossero, come le quantità Qi della produzione, degli osservabili del sistema produttivo, cioè delle grandezze misurabili. È necessario ora specificare il modo in cui queste grandezze possono essere effettivamente, o almeno in linea di principio, misurate.
Consideriamo una sfera di produzione della quale siano noti i valori M0 e C0, in termini di prezzo, del prodotto complessivo e del capitale costante impiegato, la produzione q e il tempo di lavorazione t0, espresso in giornate lavorative (gl), necessario a produrre quella quantità di valori d'uso. Ad esempio, potremmo avere:
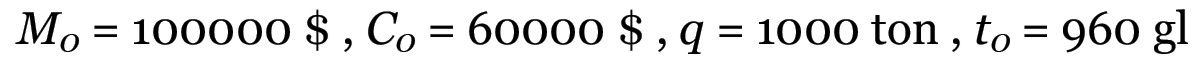
Il problema di conoscere il tempo di lavoro totale cristallizzato in questo prodotto è dato dal fatto che non conosciamo a priori il tempo di lavoro contenuto nel capitale costante C0. D'altra parte, in una frazione M1 del prodotto pari a 60000 $ sarà contenuto evidentemente lo stesso tempo di lavoro cristallizzato nel capitale costante C0. Questa frazione avrebbe i seguenti parametri:

Questi sono stati ottenuti considerando che il rapporto tra il valore del capitale merce ed il tempo di lavoro aggiunto è una costante caratteristica di ogni sfera produttiva ad un dato grado di sviluppo delle forze produttive, per cui deve essere M1/t1 = M0/t0. Chiamando K questo rapporto si ha che nel caso in esame K = 104.167, per cui t1 assume il valore indicato. Inoltre, è chiaramente costante anche il rapporto C1/M1 = C0/M0 ≡ ϑ , che nel nostro caso vale: ϑ = 6/10. Ora, possiamo affermare che il prodotto complessivo conterrà un tempo di lavoro pari a t0 + t1 = 1536 più quello contenuto nel capitale costante C1. È evidente a questo punto che reiterando il procedimento otteniamo una successione del tipo:

Ora, ti+1 può essere scritto come:
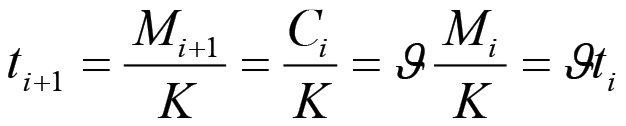
Pertanto la successione dei ti assume la forma:
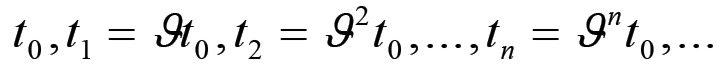
ed il tempo di lavoro totale cristallizzato nel prodotto è dato dalla somma:
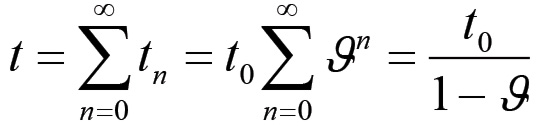 (1.14)
(1.14)
Si noti che questa serie converge al valore finito indicato nella (1.14) grazie al fatto che si ha sempre ϑ < 1. Nel caso particolare dell'esempio precedente si avrà quindi t = 2400 giornate lavorative. Con ciò si conclude la nostra dimostrazione che il valore è effettivamente un osservabile. Alla stessa conclusione si perviene in modo elementare considerando che, se è noto il rapporto W/t0 tra il valore prodotto ex-novo W = M - C, in termini di prezzo, ed il tempo di lavoro aggiunto, allora deve essere:
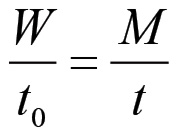 (1.15)
(1.15)
per cui:
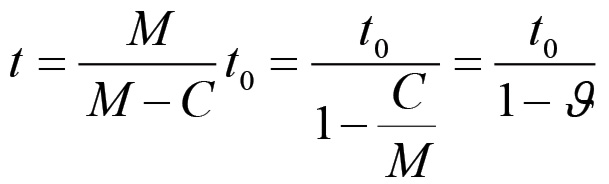
Il procedimento adottato nella dimostrazione iniziale ci consente tuttavia di comprendere più a fondo il modo in cui sono collegate le diverse sfere della produzione. Infatti, se consideriamo M1 come il capitale costante effettivo nella sua forma propria, esso sarà nel caso più semplice il prodotto di un'altra sfera di produzione, per cui sarà a sua volta soggetto ad una scomposizione che però differirà in generale da quella relativa ad M0. Ad esempio, potremmo avere:
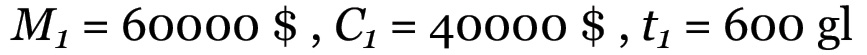
Pertanto, nella realtà, la successione dei ti è completamente diversa rispetto alla successione da noi ricavata. L'importanza della dimostrazione sta tuttavia proprio in questo, cioè nel fatto che le due serie convergeranno comunque al valore previsto t.
1.3 - Il meccanismo di riproduzione
Il meccanismo della riproduzione materiale comprende in primo luogo l'insieme delle sfere di produzione che concorrono alla formazione del prodotto complessivo sociale, in secondo luogo la sfera del consumo individuale. In quest'ultima avvengono la riproduzione della forza lavoro, cioè la ricostituzione della capacità lavorativa dei produttori, ed il consumo passivo delle classi e dei gruppi non produttivi della società. Ciascun ramo d'industria è collegato a monte alle sfere che producono le materie prime ed i mezzi di lavoro che esso impiega, mentre a valle altri rami industriali utilizzeranno il suo prodotto come mezzo di produzione, oppure, se si tratta di un ramo associato all'industria dei beni di consumo, questo prodotto entrerà nella sfera del consumo individuale (fig. 1.1).
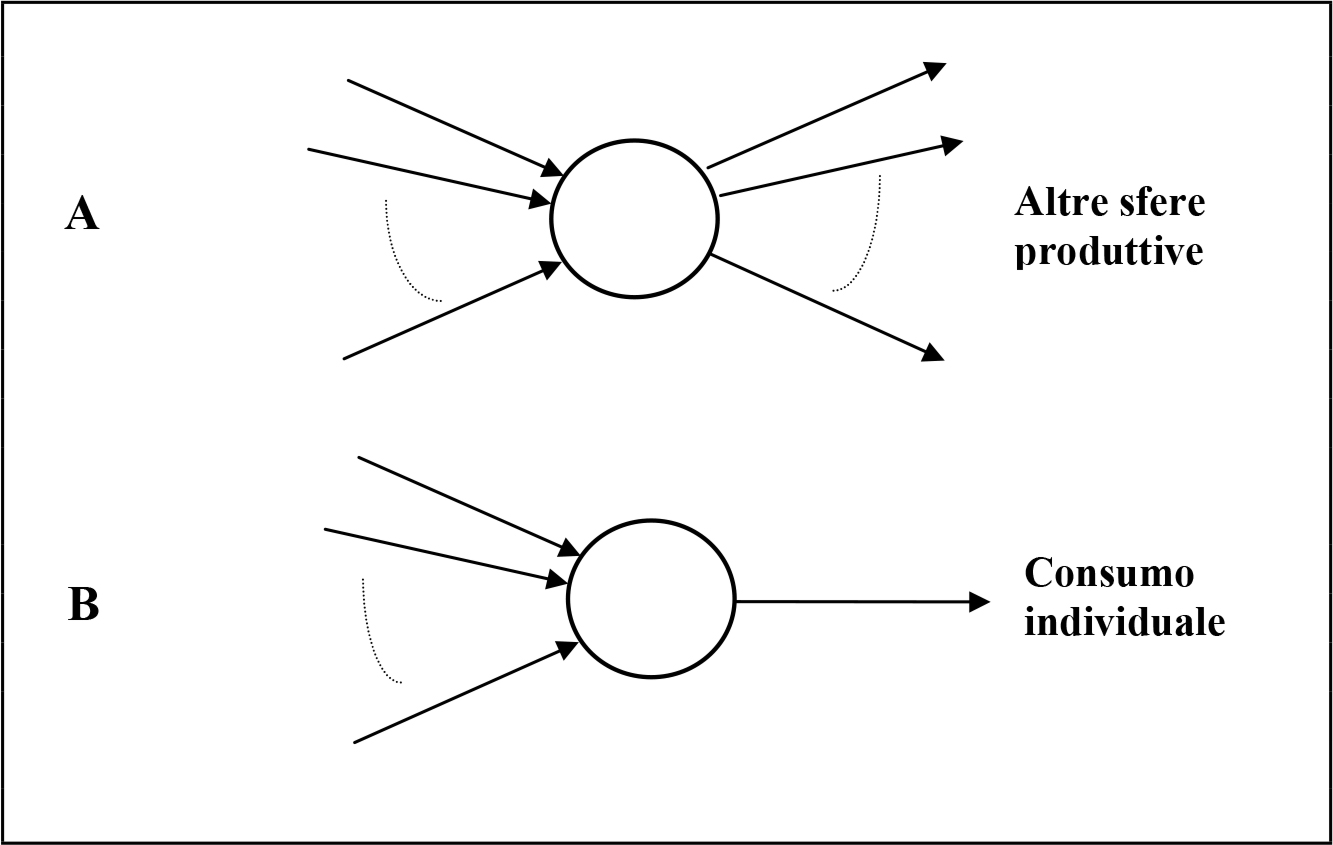 Fig. 1.1 - A: Produzione di un mezzo di produzione. B: Produzione di un bene di consumo
Fig. 1.1 - A: Produzione di un mezzo di produzione. B: Produzione di un bene di consumoNe risulta un complesso intreccio di collegamenti tra i diversi elementi che compongono il sistema di riproduzione. La fig. 1.2 mostra l'aspetto che potrebbe assumere un sistema composto da sole sette sfere produttive (nella realtà queste sono parecchie centinaia). In essa possiamo notare la presenza di cinque sfere i cui prodotti entrano nel processo lavorativo di altri rami industriali, dunque costituiscono mezzi di produzione, mentre due altre sfere, la 5 e la 7, appaiono come elementi terminali, per cui risultano associati alla produzione di beni di consumo. Da un punto di vista matematico, il meccanismo di riproduzione viene dunque ad essere rappresentato da un grafo orientato nel quale i nodi corrispondono alle sfere produttive, mentre la presenza di un arco (i,j) diretto dal nodo j-esimo al nodo i-esimo indica che la sfera di produzione i-esima utilizza una parte dei prodotti fabbricati nella sfera j-esima come mezzi di produzione. Infine, si suppone che gli archi liberi uscenti siano associati a beni di consumo diretti verso la sfera del consumo individuale.
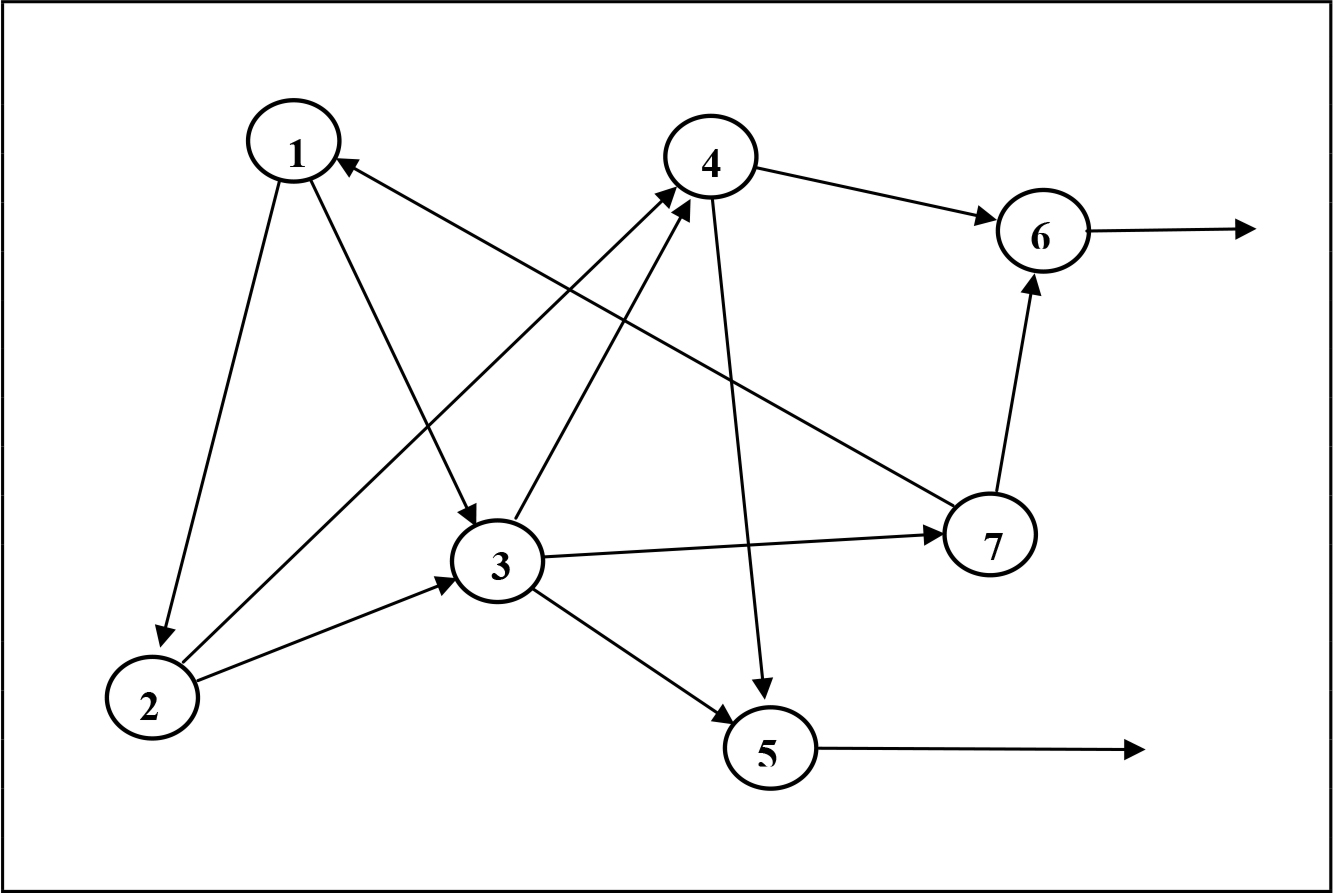 Fig. 1.2 - Ipotetico sistema di riproduzione comprendente sette sfere produttive
Fig. 1.2 - Ipotetico sistema di riproduzione comprendente sette sfere produttiveSupponiamo ora che gli scambi dei prodotti tra le diverse sfere avvengano tutti contemporaneamente al termine dell'anno corrente. Ciò equivale a considerare un periodo di rotazione annuale per tutte le sfere produttive ed a restringere la circolazione delle merci all'istante finale del ciclo di riproduzione. In questo caso l'evoluzione degli stati associati ai singoli nodi del sistema procederà in modo sincrono per tutte le sfere. Gli scambi non solo determinano l'effettiva realizzazione del valore posto nella produzione, ma pongono le basi per l'avvio di un nuovo ciclo di riproduzione l'anno successivo, in quanto le merci prodotte nel corso del ciclo attuale (mezzi di produzione e beni di consumo) verranno consumate nell'ambito del successivo ciclo di riproduzione. Sia k = 0,1,2,... un indice che identifica il generico ciclo di riproduzione e supponiamo che l'anno di partenza corrisponda al valore k = 0. Tutte le grandezze di valore, nonché i rapporti di valore, vengono quindi a dipendere da k, nel senso che la loro evoluzione sarà descritta da funzioni della variabile temporale discreta k. In particolare, l'insieme dei valori associati alla produzione di ciascuna sfera costituisce la configurazione attuale del sistema di riproduzione:
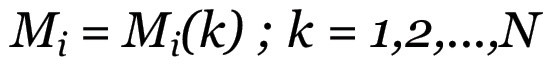
Sia ora β(k) una matrice NxN il cui generico elemento βij(k) rappresenta la frazione della produzione j-esima che viene venduta alla sfera i-esima al termine del ciclo k. Si tratta dunque di valori d'uso prodotti nella sfera j-esima e destinati ad essere utilizzati come mezzi di produzione nell'ambito del processo lavorativo della sfera i-esima al ciclo di riproduzione k+ 1. Chiaramente, se il nodo j è un nodo terminale, cioè associato alla produzione di beni di consumo, allora sarà βij = 0 per qualsiasi valore di i. Se Mj(k) è il valore prodotto nel nodo j-esimo al ciclo k e se valori d'uso provenienti da questo nodo vengono consumati come mezzi di produzione nel processo lavorativo del nodo i-esimo al ciclo k+1, allora quest'ultimo trasferirà nel suo prodotto un valore dato dalla quantità βij(k)Mj(k), corrispondente al valore dei mezzi di produzione impiegati provenienti dalla sfera j-esima. Chiaramente, se due nodi non sono collegati allora si avrà βij = 0. Per ottenere il capitale costante complessivo impiegato dalla sfera di produzione i-esima al ciclo k+1 basta dunque sommare gli N fattori βij(k)Mj(k) sull'indice j. Sommando alla grandezza ottenuta il valore prodotto ex-novo Wi(k+1) si ottiene infine il valore Mi(k+1) della produzione associata alla sfera i-esima nel corso del ciclo successivo:
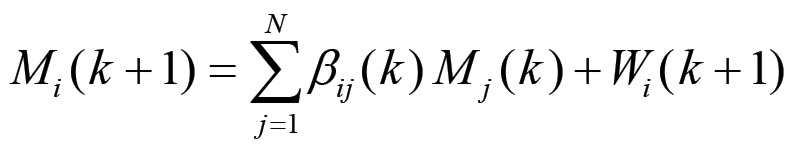 (1.16)
(1.16)
Questa formula mostra che in condizioni normali l'evoluzione del sistema è determinata, oltre che dallo stato iniziale al ciclo k = 0, dagli N2 elementi della matrice β, in quanto il valore prodotto ex-novo sta in un rapporto determinato con il capitale costante se la base tecnica del processo lavorativo non cambia. Infatti, detta Ωi = Ci/Vi la composizione organica del capitale impiegato nel nodo i-esimo ed Si = Pi/Vi il saggio del plusvalore, si ha che:
 (1.17)
(1.17)
Il parametro ωi dipende pertanto dal saggio del plusvalore e dalla composizione organica della sfera i-esima, per cui il suo valore cambia solo in seguito ad un cambiamento tecnico nel processo lavorativo. Ciò avviene in genere solo dopo un certo numero di anni, per cui su un arco di tempo più o meno lungo, corrispondente come vedremo alla durata di un periodo di espansione, queste grandezze possono essere considerate come parametri fissi del problema. La (1.16) può quindi essere riscritta nella seguente forma, che meglio mette in evidenza come l'evoluzione del sistema sia determinata dalla matrice di accoppiamento β:
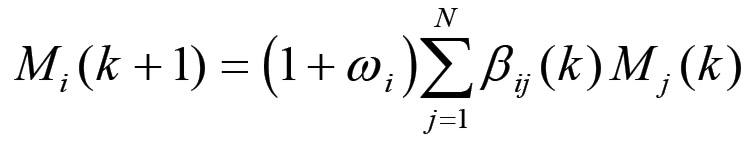 (1.18)
(1.18)
La (1.18) mette di fatto in evidenza il carattere della retroazione che determina l'evoluzione del meccanismo di riproduzione. Questa retroazione, in definitiva, è interamente determinata dai valori che assumono gli elementi della matrice di accoppiamento al termine di un ciclo k. La fig. 1.3 mostra l'aspetto che assume il sistema retroazionato associato al grafo di fig. 1.2.
Vogliamo ora stabilire in quali condizioni un meccanismo di riproduzione possa essere considerato in equilibrio. Consideriamo innanzitutto una singola sfera produttiva, poniamo la sfera i-esima, e supponiamo sia assegnata la matrice di accoppiamento . La domanda di mezzi di produzione proveniente dal generico nodo i-esimo determina evidentemente la grandezza del capitale costante che verrà impiegato nel corso dell'anno successivo nell'ambito di questa sfera. Essa è data da:
 (1.19)
(1.19)
Se Ωi è la composizione organica del capitale impiegato nella i-esima sfera produttiva, allora dovrà essere acquistata forza
lavoro, mediante un
anticipo di salari, per un valore pari a:
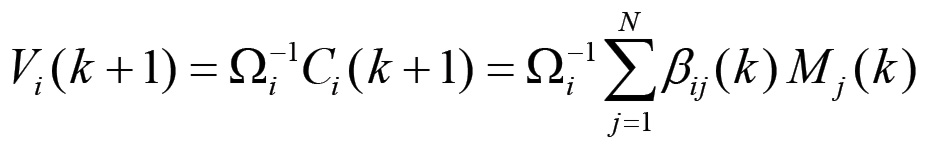 (1.20)
(1.20)
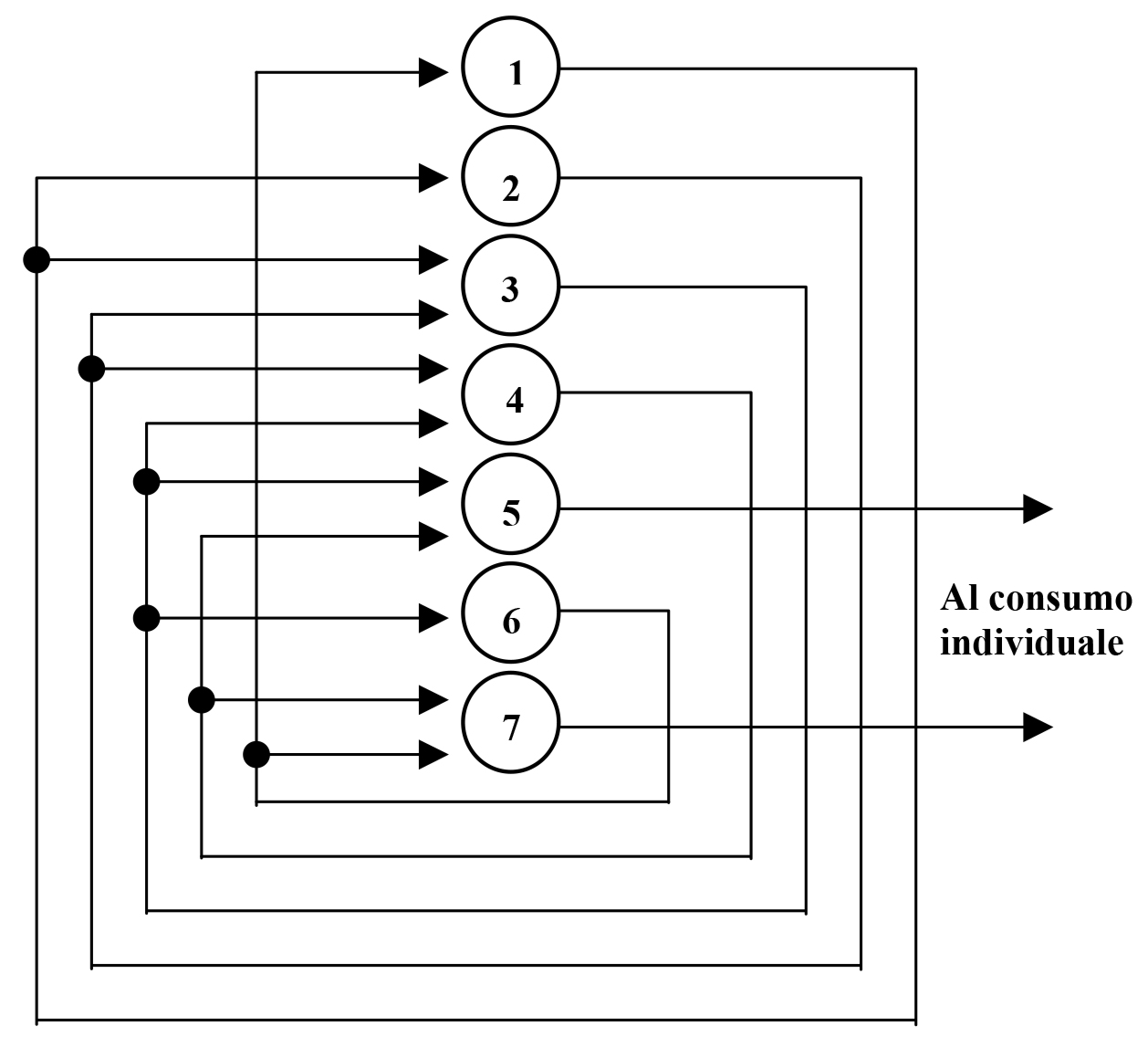 Fig. 1.3 - Forma esplicita della retroazione nelle reti. Il sistema rappresentato è lo stesso di fig. 1.2
Fig. 1.3 - Forma esplicita della retroazione nelle reti. Il sistema rappresentato è lo stesso di fig. 1.2Questi salari provvedono a loro volta a determinare una domanda di beni di consumo sul mercato, corrispondente al valore definito dalla (1.20). Complessivamente, la i-esima sfera anticipa per l'acquisto di mezzi di produzione e in salari un capitale:
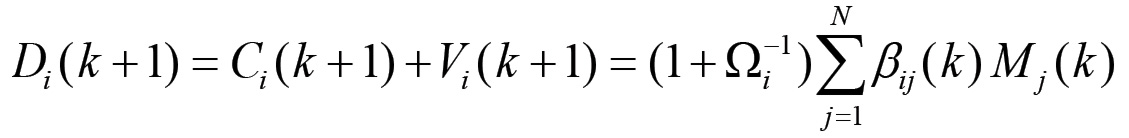 (1.21)
(1.21)
Sia ora M̃i(k) il capitale merce realizzato al termine del ciclo k da parte dei capitalisti che operano nella sfera i-esima. Si suppone qui che l'acquisto dei fattori produttivi determinato dalla (1.21), come pure l'acquisto di beni per il consumo personale di questi capitalisti tramite l'impiego di una parte del plusvalore realizzato, proceda simultaneamente alla vendita del proprio capitale merce. In certe condizioni, tuttavia, la grandezza M̃i(k) potrebbe differire dal valore Mi(k) posto nella produzione. Ciò accade quando una parte delle merci fabbricate nella sfera i-esima risulta essere sovrapprodotta, ovvero prodotta con un valore complessivo che eccede le possibilità di assorbimento da parte del mercato, oppure quando queste merci vengono prodotte in misura insufficiente rispetto alle esigenze del processo di accumulazione. Pertanto, in generale avremo che:
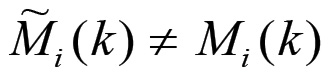
Sia ora τi il rapporto tra la massa del plusvalore ed il capitale anticipato contenuti nel prodotto della sfera i-esima. Questa grandezza in condizioni di equilibrio coincide con il saggio medio del profitto τ, almeno per quanto riguarda le sfere della produzione industriale, mentre nel caso delle produzioni soggette a rendita (agricoltura e industria mineraria) sarà sempre maggiore di τ, come avremo modo di dimostrare nel cap. III . Se D̃i(k) è il capitale anticipato (capitale costante più salari) contenuto nel capitale merce realizzato e P̃i(k) è la massa di plusvalore corrispondente, allora per definizione si ha:
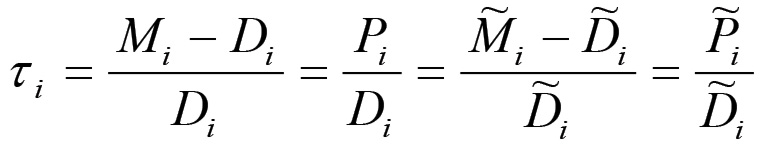
Pertanto, la massa di plusvalore contenuta nel capitale merce realizzato corrisponde ad una frazione di quest'ultimo data da:
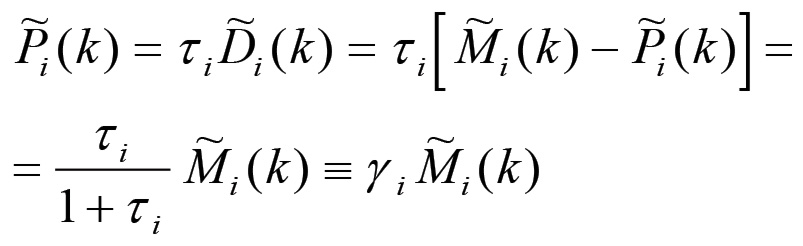 (1.22)
(1.22)
Supponiamo ora che una frazione εi di questo plusvalore venga impiegata per il consumo personale dei capitalisti. La grandezza εi è chiaramente nulla nel caso in cui i capitalisti utilizzino l'intero plusvalore come capitale addizionale nell'ambito del processo di accumulazione, mentre si avrà εi = = 1 quando tutto il plusvalore viene impiegato per il consumo personale improduttivo. Pertanto avremo in generale che 0 ≤ εi ≤ 1, anche se in casi del tutto eccezionali εi potrebbe addirittura superare l'unità, indicando che non solo l'intero plusvalore viene utilizzato per l'acquisto di beni di consumo, ma che in aggiunta a questo una parte di quello che era il capitale anticipato viene ora dirottata dall'impiego produttivo verso la sfera del consumo.
In ogni caso, si ha che la grandezza effettiva del capitale anticipato per il successivo ciclo di riproduzione sarà data dalla differenza tra il valore del capitale merce realizzato e la frazione del plusvalore destinata all'acquisto di beni di consumo:
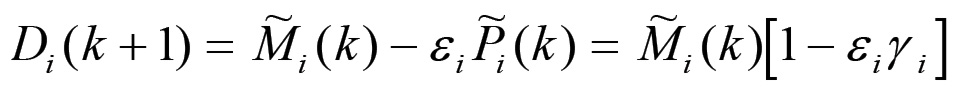 (1.23)
(1.23)
Combinando ora la (1.23) con la (1.21) si perviene al risultato fondamentale che la grandezza effettiva del capitale merce realizzato è univocamente determinata dalla matrice di accoppiamento e dalla configurazione attuale del sistema:
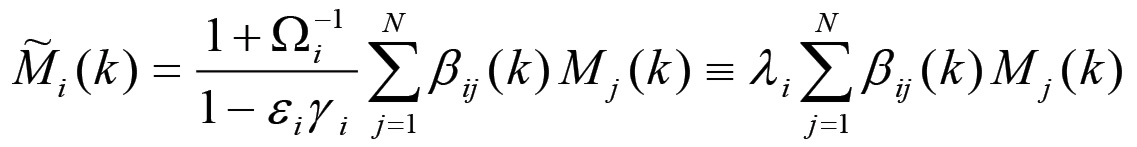 (1.24)
(1.24)
Questa equazione esprime essenzialmente l'eguaglianza tra la grandezza del capitale merce venduto, dunque realizzato, ed il valore complessivo degli acquisti operati dai capitalisti della i-esima sfera di produzione. Questi acquisti comprendono in generale forza lavoro, mezzi di produzione e beni per il consumo individuale e collettivo della classe borghese. Si prescinde dunque, almeno per ora, dai meccanismi della tesaurizzazione e del credito, i quali alterano evidentemente la legge espressa dalla (1.24).
Siamo ora in grado di impostare e discutere le condizioni di equilibrio di un sistema di riproduzione. È chiaro innanzitutto che l'equilibrio implica un bilanciamento tra il valore posto nella produzione e quello realizzato nell'ambito della circolazione.
Questa condizione può essere espressa per mezzo di N equazioni del tipo:
 (1.25)
(1.25)
ovvero, utilizzando la (1.24):
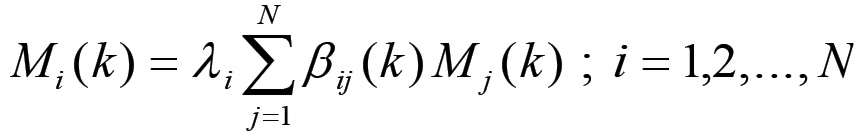 (1.26)
(1.26)
In condizioni di non equilibrio, possiamo inoltre introdurre un indice di sovrapproduzione σi(k), definito come:
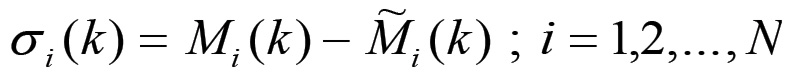 (1.27)
(1.27)
La sovrapproduzione totale sarà pertanto data dalla somma:
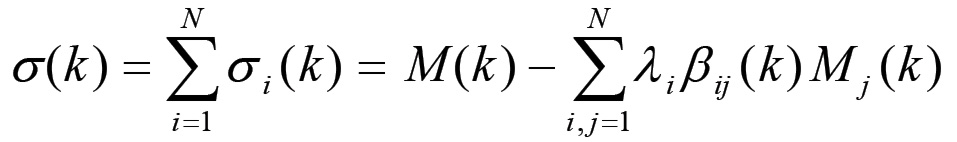 (1.28)
(1.28)
Essa è dunque interamente determinata dalla configurazione attuale e dalla matrice di accoppiamento β, una volta assegnati i parametri λ del sistema.
Torniamo ora alle condizioni di equilibrio (1.26). Esse costituiscono un sistema omogeneo di N equazioni nelle variabili configurazionali Mi che può essere scritto nella forma:
 (1.29)
(1.29)
dove gli elementi della matrice ξ = [ξij] sono definiti come:
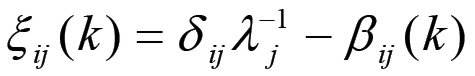 (1.30)
(1.30)
e δij è il delta di Krönecker:

Un sistema del tipo (1.29) ammette una soluzione non banale se e solo se il determinante della matrice dei coefficienti è nullo. Pertanto, le condizioni di equilibrio comportano l'esistenza di un vincolo sui possibili valori degli elementi della matrice di accoppiamento β. Questo vincolo è dato dalla condizione di annullamento del determinante della matrice ξ, ovvero:
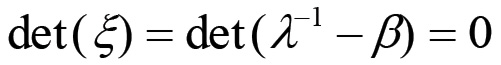 (1.31)
(1.31)
dove λ-1 è la matrice diagonale: λ-1 = [δijλj-1]. Consideriamo ora più da vicino la matrice β. Se r < N è il numero di sfere impegnate nella produzione di mezzi di produzione, non si perde in generalità imponendo una numerazione dei nodi del grafo associato al sistema di riproduzione fatta in modo tale che se 1 ≤ i ≤ r allora il nodo corrispondente rappresenta una produzione di mezzi di produzione, mentre per r < i ≤ N si hanno solo nodi relativi alla produzione di beni di consumo. Poiché la i-esima colonna della matrice β contiene le frazioni della produzione i-esima che vengono vendute come mezzi di produzione a tutte le altre sfere, allora è chiaro che le ultime N - r colonne devono contenere solo elementi nulli, in quanto si riferiscono a beni di consumo. Per quanto riguarda le prime r colonne, invece, l'equilibrio di mercato implica che la somma di tutti gli elementi di una colonna deve essere uguale ad 1:
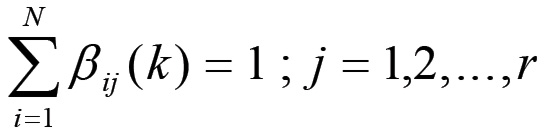 (1.32)
(1.32)
Queste r equazioni costituiscono altrettanti vincoli sulla matrice β in condizioni di equilibrio. Ora, la domanda diretta e indotta (tramite i salari) di beni di consumo determinata da una sfera associata alla produzione di mezzi di produzione è in base alla (1.19) ed alla (1.24) data da:

La domanda totale di beni di consumo indotta dall'insieme delle sfere impegnate nella produzione di mezzi di produzione si ottiene da questa espressione sommando sull'indice i = 1,2 ,...,r. Questo valore determina un flusso di denaro dalle prime r sfere verso i nodi associati alla produzione di beni di consumo. Indipendentemente dalla esistenza o meno di una situazione di equilibrio, questo flusso deve essere controbilanciato da un flusso opposto, associato all'acquisto di mezzi di produzione da parte dei capitalisti che operano nella produzione di beni di consumo. In altri termini, la domanda complessiva di beni di consumo proveniente dai rami associati alla produzione di mezzi di produzione deve coincidere con la domanda di mezzi di produzione proveniente dalle sfere associate alla produzione di beni di consumo:
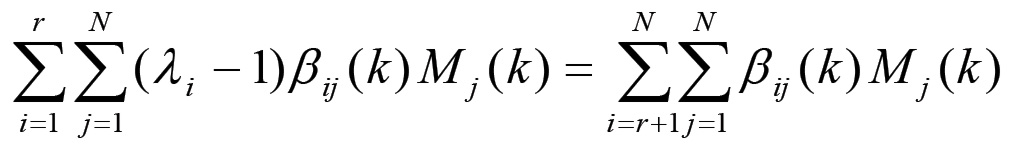 (1.33)
(1.33)
Scambiando le sommatorie e portando tutti i fattori al primo membro, la (1.33) può essere riscritta come segue:
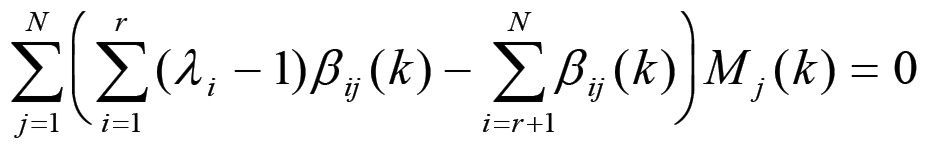 (1.34)
(1.34)
Infine, con un ulteriore passaggio, si ha:
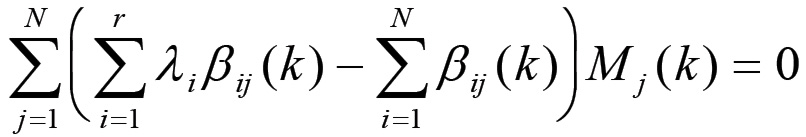 (1.35)
(1.35)
Questa è l'equazione fondamentale che assicura la consistenza del sistema, ovvero la consistenza tra la configurazione assegnata ed i valori che assumono gli elementi della matrice di accoppiamento. L'equazione (1.35) ha la forma di una condizione di annullamento per una particolare combinazione lineare degli elementi della configurazione attuale. Una possibile soluzione consiste nell'imporre che i coefficienti della sommatoria siano tutti identicamente nulli:
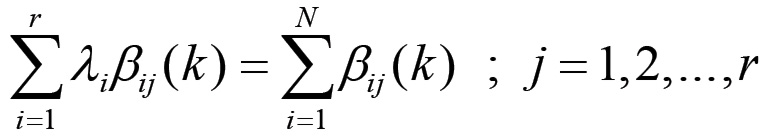 (1.36)
(1.36)
Se il sistema (1.36) di r equazioni risulta essere soddisfatto da una particolare combinazione degli elementi della matrice di accoppiamento, allora l'equazione di consistenza (1.35) è soddisfatta per ogni scelta arbitraria della configurazione attuale. In questo caso tuttavia si hanno delle restrizioni sulle possibili forme del grafo associato al sistema di riproduzione.
Infatti, dalla (1.34) risulta ora che deve essere:
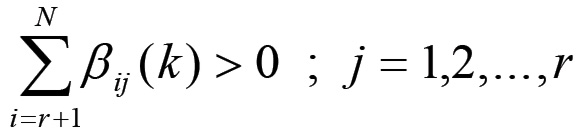 (1.37)
(1.37)
in quanto si ha sempre λi > 1. La (1.37) implica che per ogni nodo associato alla produzione di mezzi di produzione, esiste almeno un elemento non nullo della matrice di accoppiamento che rappresenta un arco diretto verso una sfera associata alla produzione di beni di consumo. In altri termini in questo caso, cioè nel caso in cui l'equazione di consistenza (1.35) è soddisfatta da un'arbitraria configurazione del sistema, ogni sfera relativa alla produzione di mezzi di produzione è collegata ad almeno una sfera associata alla produzione di beni di consumo. Chiameremo sistema del primo tipo un meccanismo di riproduzione che soddisfa questa condizione. Nel caso generale, invece, i coefficienti della combinazione lineare (1.35) non sono tutti identicamente nulli, per cui la matrice di accoppiamento viene a dipendere dalla configurazione attuale, nel senso che esiste un vincolo sui possibili valori che essa assume. Questo vincolo sarà appunto imposto dalla configurazione attuale del sistema. Chiameremo pertanto sistema del secondo tipo un meccanismo di riproduzione nel quale esistono nodi collegati esclusivamente a sfere che producono mezzi di produzione.
Notiamo ora che nel caso di un sistema del primo tipo, le condizioni di equilibrio (1.32) implicano che:
 (1.38)
(1.38)
In questo caso, dunque, esistono all'equilibrio 2r equazioni vincolari sulla matrice β, e le sfere associate alla produzione di mezzi di produzione risultano essere in equilibrio effettivo comunque si scelga la r-pla (M1(k), M2(k),...,Mr(k)).
Infatti, per la (1.32) si ha che la vendita totale di mezzi di produzione è data da:
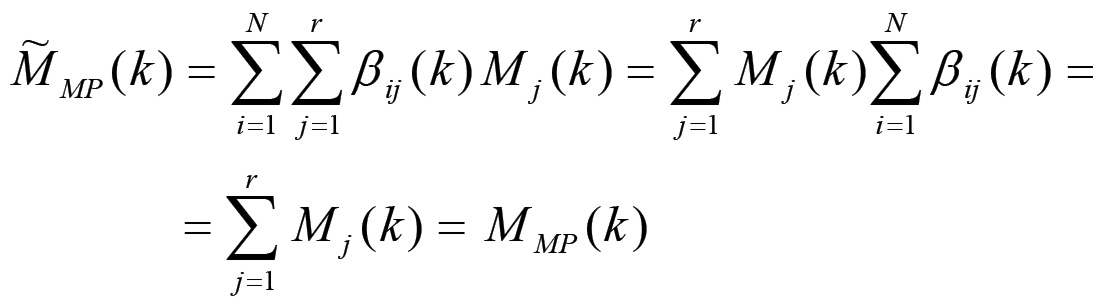
mentre la (1.38) assicura la consistenza del sistema indipendentemente dalla scelta della configurazione attuale. Le rimanenti N - r variabili configurazionali possono a questo punto essere determinate risolvendo il sistema (1.29).
Consideriamo ora un sistema del primo o del secondo tipo in equilibrio al generico ciclo k. La configurazione del sistema al ciclo k + 1 è determinata, come sappiamo, dalle equazioni (1.18). Poiché in questo caso valgono anche le equazioni di equilibrio (1.26), allora è possibile stabilire una relazione diretta tra la configurazione attuale di un generico nodo e la sua configurazione successiva. Infatti, combinando la (1.18) e la (1.26) si ottiene:
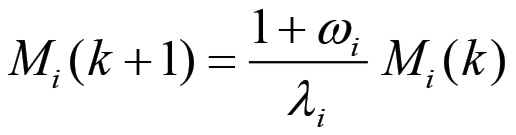 (1.39)
(1.39)
Questa equazione implica che in condizioni di equilibrio ogni variabile configurazionale evolve ad un tasso differente, determinato dal parametro (1+ωi)λi-1, il quale assume in generale valori diversi passando una sfera all'altra. È semplice valutare il significato di questi parametri. Poiché:
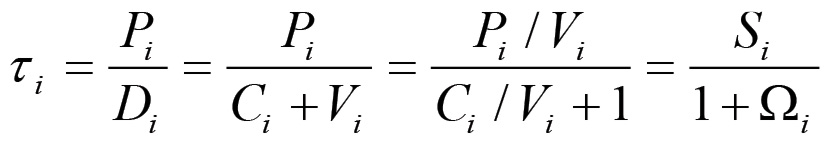
allora si ha che:
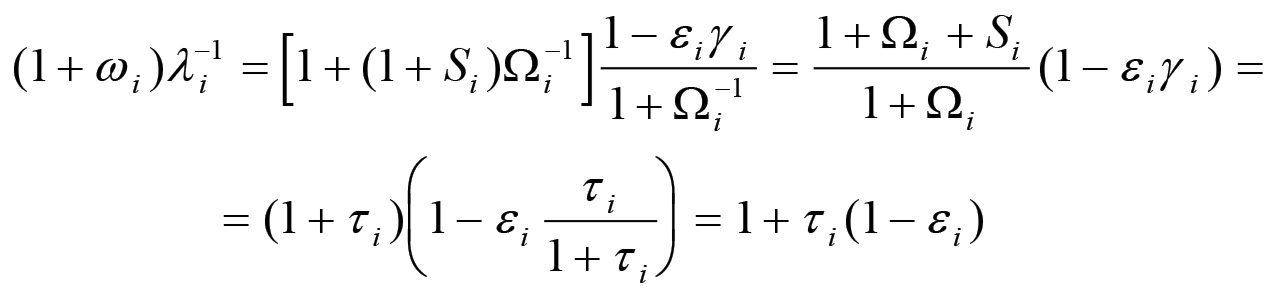
Ne consegue che il tasso di aumento del valore della produzione i-esima è determinato, in condizioni di equilibrio, dalla grandezza τi, dunque dal saggio medio del profitto nel caso di una produzione non soggetta a rendita. Inoltre esso dipende dal grado di trasformazione del plusvalore in capitale addizionale, cioè dalla grandezza 1 - εi che vale 1 nel caso in cui viene accumulato l'intero plusvalore, mentre vale zero quando questo viene utilizzato interamente per il consumo personale dei capitalisti. Definiamo pertanto saggio di accumulazione della sfera i-esima la grandezza:
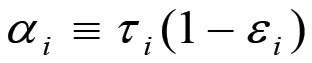 (1.40)
(1.40)
In base a questa definizione la (1.39) può quindi essere riscritta come segue:
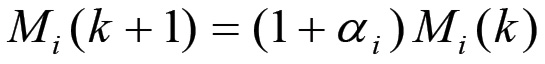 (1.41)
(1.41)
Ci chiediamo ora se la nuova configurazione, ottenuta mediante la (1.41), corrisponde ancora ad una configurazione di equilibrio. Ciò si verifica se essa soddisfa il sistema di equazioni (1.26):
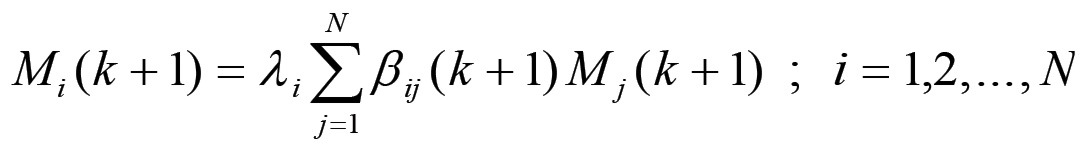
e la matrice β(k+1) soddisfa le equazioni di consistenza ed equilibrio. Sostituendo le (1.41) il sistema assume la forma:
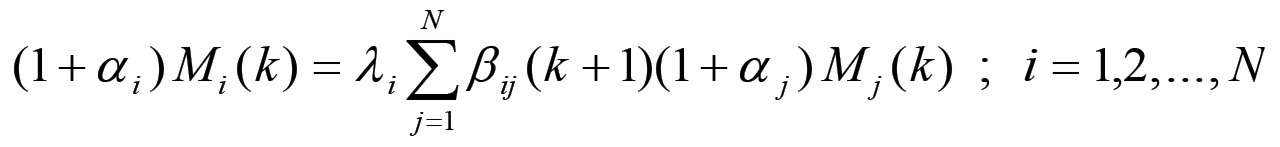
Scrivendo ora queste equazioni come segue:
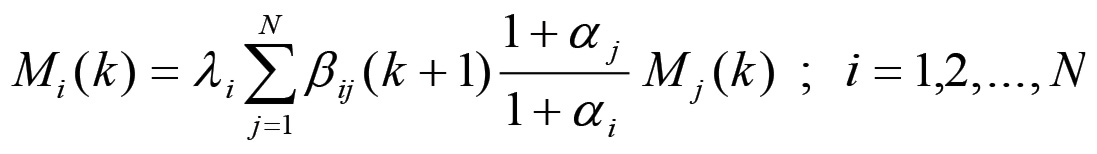
si vede che affinché la nuova N-pla {Mi(k + 1); i = 1,2,...,N} corrisponda ad una configurazione di equilibrio, la matrice β' i cui elementi sono definiti come:
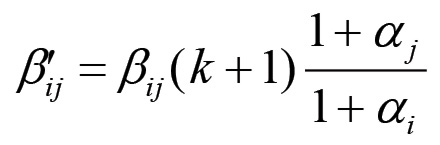
deve soddisfare le equazioni di consistenza ed equilibrio. Ciò avviene chiaramente nel caso in cui αi = α per ogni valore dell'indice i, cioè nel caso in cui il tasso di accumulazione sia uguale per tutte le sfere di produzione. In queste condizioni si ha che la matrice di accoppiamento risulta essere indipendente dal tempo:
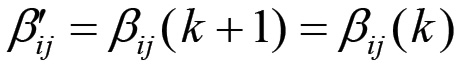
Questa condizione si verifica, in particolare, quando il tasso di accumulazione è nullo in tutti i rami industriali. In quest'ultimo caso diciamo che la riproduzione si svolge su scala semplice. Vogliamo ora dimostrare che affinché il meccanismo di riproduzione si mantenga in uno stato di equilibrio, è non solo sufficiente ma anche necessario che il saggio di accumulazione sia uniforme in tutte le sfere che producono mezzi di produzione. Inoltre, questo saggio deve coincidere con il tasso medio di accumulazione delle sfere associate alla produzione di beni di consumo.
Per dimostrare questo teorema, supponiamo che la matrice β' soddisfi le r condizioni di equilibrio (1.32):

In questo caso si ha che la matrice β(k + 1) soddisfa le equazioni:
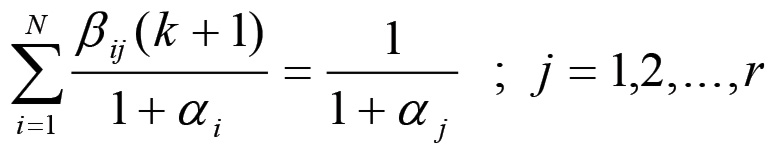
Poiché la matrice β(k + 1) soddisfa anch'essa le condizioni di equilibrio (1.32), ciascuna di queste equazioni mostra che la media ponderata degli N fattori positivi 1/(1 + αi), effettuata utilizzando come pesi gli elementi della j-esima colonna della matrice β(k + 1), coincide con il j-esimo fattore 1/(1 + αj). Poniamo ora per comodità: xi ≡ 1/(1 + αi). Il sistema precedente assume dunque la forma:
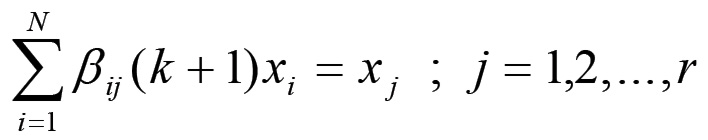 (1.42)
(1.42)Raggruppiamo inoltre tutte le sfere relative alla produzione di beni di consumo in un'unica sfera. Il saggio di accumulazione α di questo nodo è dato da una media ponderata dei saggi individuali delle diverse sfere. Infatti, ponendo:
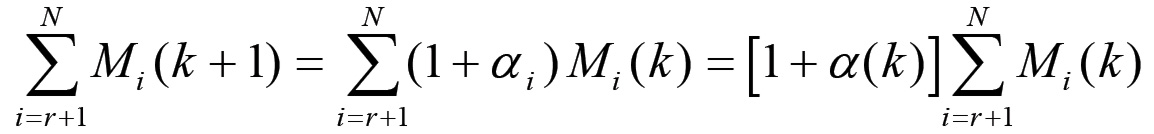
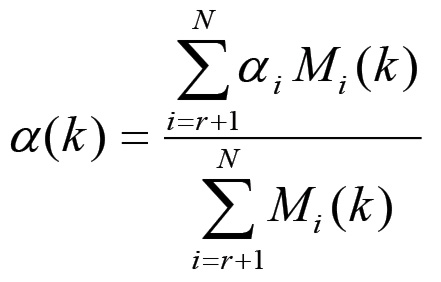 (1.43)
(1.43)si ha:
Si noti che, per definizione, i saggi di accumulazione i sono parametri del problema indipendenti da k, mentre il saggio medio di accumulazione viene a dipenderne, in quanto come si osserva nella formula (1.43) i pesi della media sono in generale funzioni della variabile temporale k.
Poniamo ora:
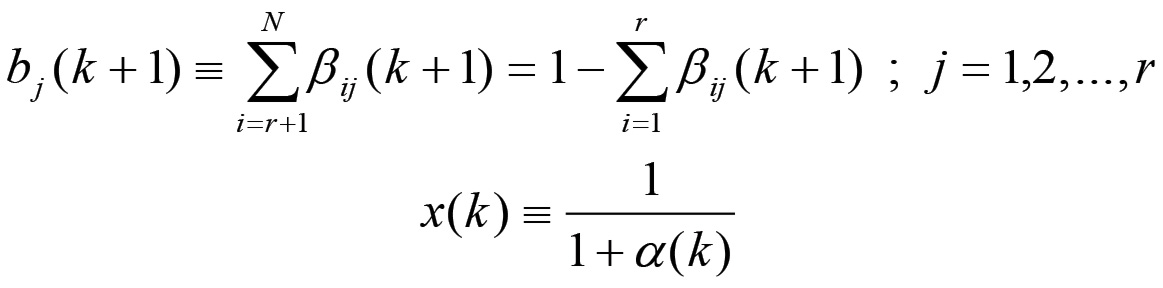
Il parametro bj è la frazione della produzione del nodo j-esimo diretta verso le sfere impegnate nella produzione di beni di consumo. Per quanto riguarda la variabile x, si ha che:
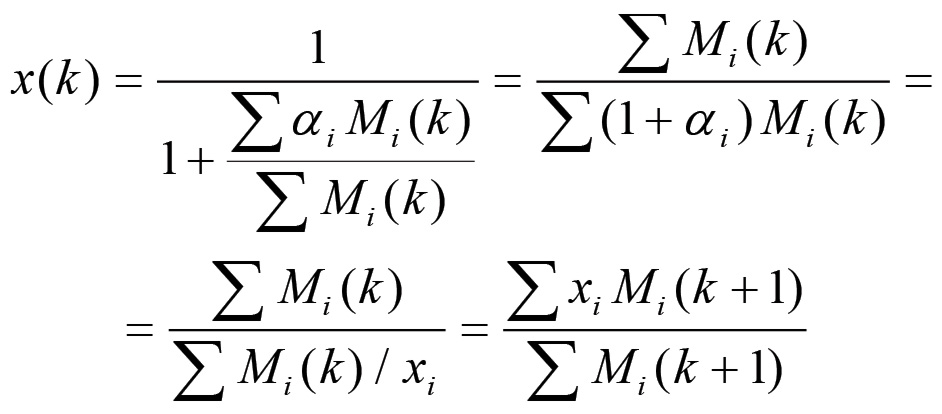
L'ultimo passaggio segue dalla (1.41) e dalla definizione dei parametri xi. Esso mostra che x(k) coincide sia con la media armonica delle xi al ciclo k, sia con la media ponderata degli stessi parametri al ciclo k+1. Poiché la media armonica, a parità di pesi, è sempre minore o uguale alla media ponderata semplice, allora si ha che, per ogni k:
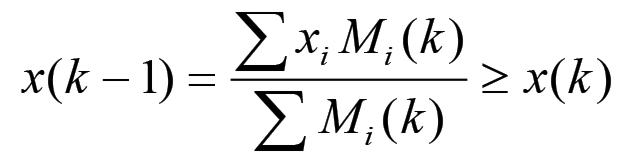
Essendo inoltre per ogni k: Mi(k + 1) ≥ Mi(k), arriviamo alla conclusione che la funzione x = x(k) è decrescente all'aumentare dei pesi. Ciò implica che il tasso medio di accumulazione dei nodi associati alla produzione di beni di consumo deve soddisfare la regola:

per ogni valore del parametro temporale k. Ora, il valore del capitale merce associato ad un nodo è sempre chiaramente maggiore del valore dei mezzi di produzione che questo ramo industriale acquisterà al ciclo successivo da qualsiasi altra sfera di produzione. In particolare, avremo sempre che:

Ciò significa che x(k) deve soddisfare la seguente diseguaglianza per ogni valore dell'indice j:

In altri termini, risulta verificato il seguente set di diseguaglianze:
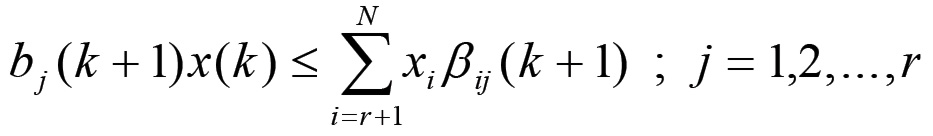
Consideriamo ora il capitale costante complessivamente impiegato nei nodi che producono beni di consumo. Esso, al ciclo k + 1, è dato da:

D'altra parte, si ha anche:
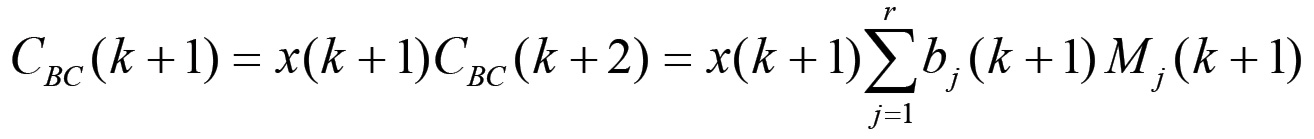
Confrontando queste due espressioni si arriva alla conclusione che deve essere:

Essendo x(k + 1) ≤ x(k) si ottiene infine:
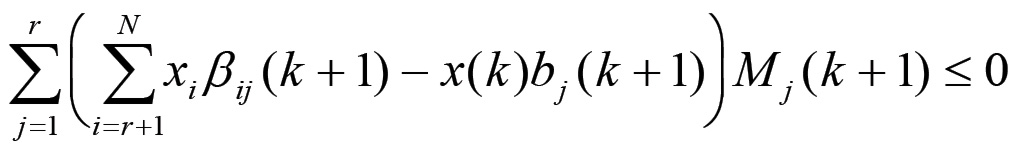
I coefficienti di questa combinazione lineare sono, in base a quanto ricavato precedentemente, tutti positivi o nulli, per cui questa diseguaglianza impone che essi siano tutti effettivamente nulli, ovvero che valga il sistema di equazioni:
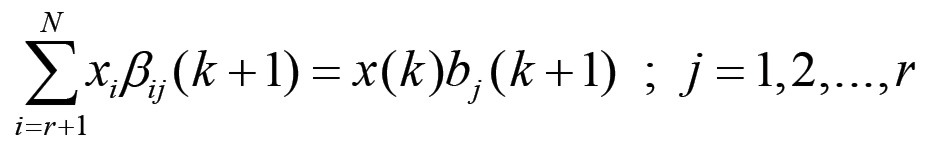
Ciò implica che il sistema (1.42) può essere riscritto nella forma:
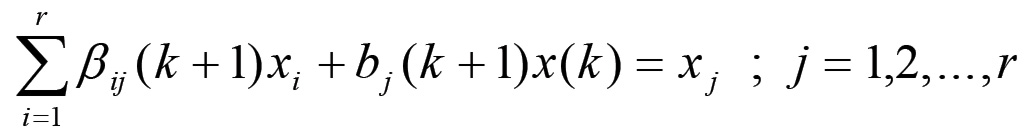
Pertanto xj coincide con la media ponderata di r + 1 elementi, tra i quali compare xj stesso. Siano ora n ed m due indici tali che xn = min{x1, x2, ..., xr } e xm = max{x1, x2, ..., xr }. Se x < xm, allora per j = m si ha che l'equazione:
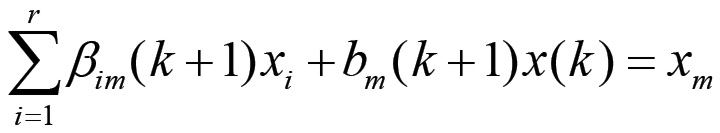
non può mai essere soddisfatta in quanto la media di un insieme di valori non tutti uguali non può coincidere con l'estremo superiore di questo insieme.
Analogamente, se x ≥ xm, allora per j = n non potrà essere soddisfatta la corrispondente equazione, in quanto la media non può coincidere neanche con l'estremo inferiore. Pertanto, se i saggi di accumulazione αi ed α non coincidono per ogni i = 1,2,...,r, il sistema di condizioni (1.42) non potrà essere soddisfatto ed il meccanismo di riproduzione non potrà conservare lo stato di equilibrio. In altri termini, se il saggio di accumulazione non è uniforme ogni configurazione di equilibrio evolverà verso una nuova configurazione per la quale non esiste una matrice di accoppiamento che assicuri l'equilibrio del sistema di riproduzione. Ciò conclude la dimostrazione del teorema.
I risultati ottenuti in questo paragrafo ci consentono in definitiva di stabilire se un meccanismo di riproduzione si trova in uno stato di equilibrio e in quali condizioni esso conserva questo stato. L'evoluzione dei sistemi di riproduzione in condizioni di non equilibrio verrà invece affrontata più avanti nel IV capitolo, in quanto questo tipo di analisi richiede delle considerazioni aggiuntive e lo studio preliminare dei meccanismi della rendita e del credito. In questo contesto sarà in particolare possibile determinare le cause del disequilibrio ed i meccanismi di compensazione che rendono possibile lo svolgimento del processo di accumulazione.
1.4 - Riproduzione semplice
Lo studio del complesso intreccio di collegamenti nel quale si sviluppa il meccanismo della riproduzione materiale può essere notevolmente semplificato se si raggruppano da una parte tutte le sfere che producono mezzi di produzione, dall'altra quelle che producono beni di consumo. In questo caso il sistema assume la forma di un grafo a due nodi, e le due grandi sezioni della riproduzione che si ottengono sono alla base degli schemi di Marx della riproduzione semplice ed allargata. Parliamo in generale di riproduzione semplice quando il saggio di accumulazione è nullo per tutte le sfere di produzione. Osservando la (1.40) si vede che questa situazione si verifica quando εi = 1 per ogni valore dell'indice i, ovvero quando la classe borghese utilizza l'intero plusvalore per il consumo improduttivo. L'acquisto di beni di consumo avviene sia come acquisto diretto da parte dei capitalisti, finalizzato al consumo privato, sia attraverso la spesa dello Stato in armamenti, stipendi, opere pubbliche etc. In quest'ultimo caso la frazione del plusvalore che viene prelevata dallo Stato a vario titolo viene spesa collettivamente dalla classe borghese al fine di garantire il supporto necessario al normale svolgimento del processo di produzione. Osservando la (1.41) si vede immediatamente che in un ciclo di riproduzione semplice la configurazione del sistema resta invariata, per cui il processo di accumulazione risulta momentaneamente sospeso. Lo studio del meccanismo di riproduzione quando la scala della produzione resta invariata costituisce pertanto un punto di partenza per la descrizione di periodi di recessione e ristrutturazione del sistema produttivo.
Consideriamo dunque il sistema a due nodi rappresentato in fig. 1.4. La struttura di questo grafo mostra che il nodo 1 è associato alla produzione di mezzi di produzione (cioè mezzi di lavoro e materie prime), mentre nel nodo 2 sono raggruppate tutte le sfere relative alla produzione dei beni di consumo (mezzi di sussistenza per i lavoratori, beni di lusso etc.).
 Fig. 1.4 - Il sistema a due nodi: 1 = mezzi di produzione; 2 = beni di consumo.
Fig. 1.4 - Il sistema a due nodi: 1 = mezzi di produzione; 2 = beni di consumo.Si tratta evidentemente di un sistema del primo tipo, per cui l'equazione di consistenza in condizioni di equilibrio assume la forma del sistema di equazioni 1.38. Nel nostro caso, essendo r = 1 e β12 = β22 = 0, il sistema si riduce alla singola equazione:
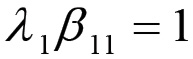 (1.44)
(1.44)la quale, associata all'equazione di equilibrio:
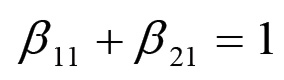 (1.45
(1.45consente di determinare univocamente la matrice di equilibrio in funzione dei parametri del sistema. Per quanto riguarda la matrice , le sue componenti sono date da:
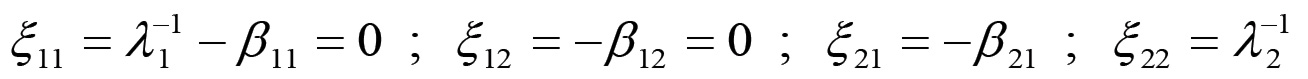
In questo caso il determinante det() è sempre nullo e si ha che la configurazione di equilibrio soddisfa l'equazione:

Ovvero:
 (1.46)
(1.46)Poniamo ad esempio:
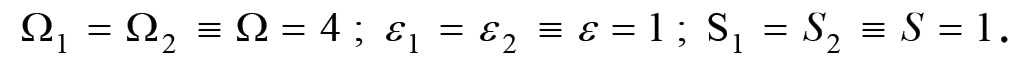
Con questa scelta dei parametri si ha che:
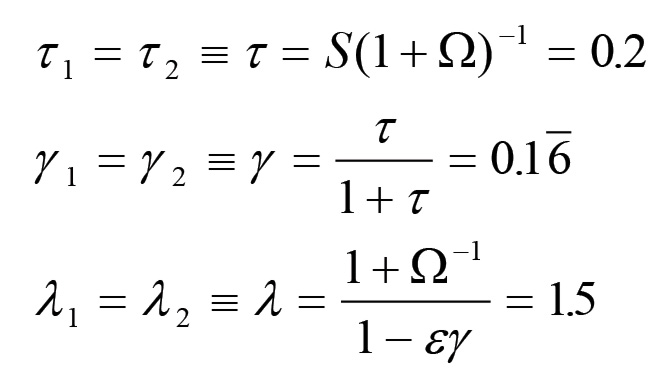
Pertanto le matrici β e ξ assumono i valori:
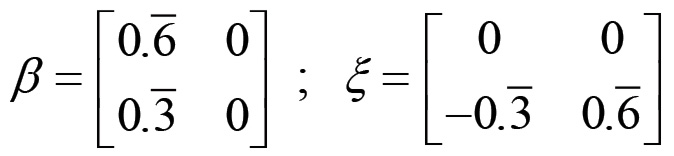
Se ora poniamo M1 = 5000 Mgl (milioni di giornate lavorative), allora per la (1.46) M2 deve essere pari a 2500 Mgl.
La composizione di questi capitali può essere ricavata utilizzando le formule:
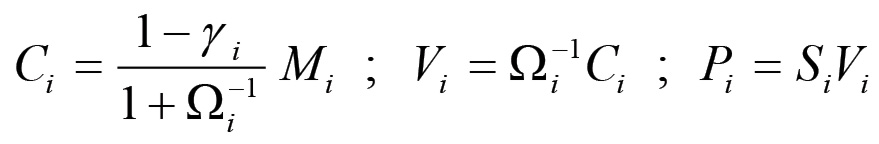
Si ottiene in definitiva il seguente schema di Marx, il quale rappresenta un meccanismo di riproduzione semplice in equilibrio stabile:

Si noti che il nodo 1 produce da solo l'intera massa di mezzi di produzione necessaria. Il capitale costante complessivo utilizzato annualmente dalla società coincide quindi con la produzione della sezione I. Nel caso in esame questa produzione ha un valore costante, per cui un sistema di riproduzione semplice può essere definito come un sistema per il quale il valore del capitale costante complessivo impiegato dalla società è invariante:
 (1.47)
(1.47)Si noti che se C(k+1) è il valore che i mezzi di produzione trasferiscono nel prodotto al ciclo k+ 1, allora questa grandezza coincide con la domanda di mezzi di produzione al termine del ciclo k, per cui la (1.47) esprime semplicemente il fatto che, in un meccanismo di riproduzione semplice, la domanda totale di nuovi mezzi di produzione eguaglia il valore C(k) trasferito dai mezzi di produzione impiegati nel ciclo attuale:
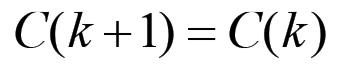 (1.48)
(1.48)La soluzione di questa equazione coincide evidentemente con la (1.47). Supponiamo ora che non si verifichino mutamenti nella struttura del sistema produttivo, dunque che la forza produttiva del lavoro, la composizione organica media del capitale ed il saggio generale del plusvalore restino invariati. In questo caso la (1.47) implica che tutte le altre grandezze e rapporti di valore restano costanti nel tempo. Infatti, detta Ω la composizione organica media del capitale complessivo si ha:
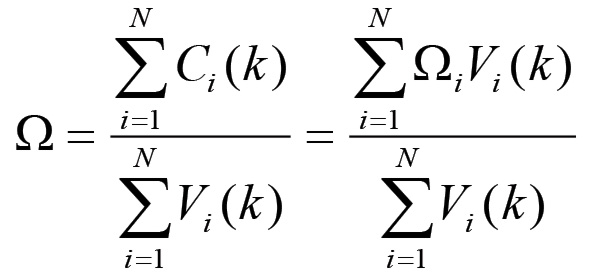 (1.49)
(1.49)Pertanto, se Ω è costante allora:
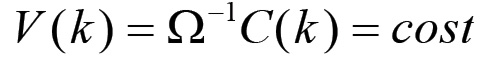 (1.50
(1.50ovvero anche il capitale variabile complessivo rimane costante. Inoltre, detto S il saggio generale del plusvalore, si ha che:
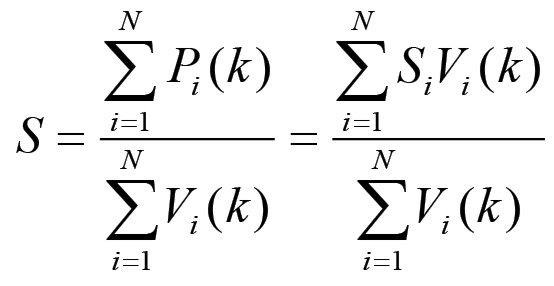 (1.51)
(1.51)per cui se anche S è invariante allora la stessa massa totale del plusvalore resta invariata:
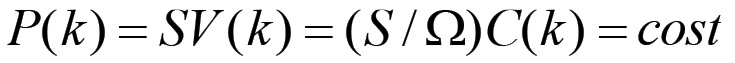 (1.52)
(1.52)L'invarianza di C, V e P comporta infine l'invarianza della produzione totale M:
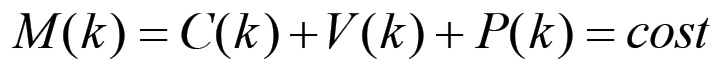 (1.53)
(1.53)Questo stesso risultato può ovviamente essere ricavato in modo indipendente utilizzando le equazioni di evoluzione della configurazione (1.41). Come abbiamo visto nel paragrafo precedente, affinché il sistema di equazioni che esprime la dinamica del meccanismo di riproduzione sia consistente, la domanda complessiva di beni di consumo proveniente dai rami associati alla produzione di mezzi di produzione deve coincidere con la domanda di mezzi di produzione proveniente dalle sfere associate alla produzione di beni di consumo. L'espressione matematica di questa eguaglianza è come sappiamo l'equazione di consistenza (1.35). Nel caso del sistema a due nodi questa equazione può essere messa in una forma che esprime più chiaramente il rapporto esistente tra le due grandi sezioni della riproduzione materiale. Se la riproduzione si svolge su scala semplice, allora la domanda complessiva di beni di consumo proveniente dai lavoratori e dai capitalisti della sezione I è data dal valore prodotto ex novo in questa sezione nel corso del ciclo attuale, dunque da W1(k) = V1(k) + P1(k). Affinché il meccanismo sia consistente, questo valore deve eguagliare il valore del capitale costante che verrà in seguito impiegato nel settore II, dunque C2(k+1). L'equazione di consistenza, nel caso della riproduzione semplice, assume quindi la forma seguente:
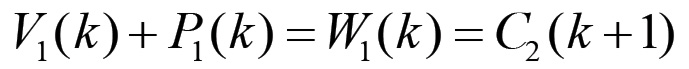 (1.54)
(1.54)D'altra parte, sappiamo che nel contesto della riproduzione semplice tutte le grandezze sono invarianti rispetto a k. In particolare si ha che C2(k+1) = C2(k), cosicché perveniamo al seguente risultato:
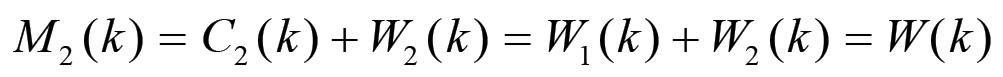 (1.55)
(1.55)L'equazione di consistenza impone dunque che il capitale merce prodotto nella sezione II nel corso di un ciclo di riproduzione semplice eguagli il valore totale prodotto ex-novo in entrambe le sezioni.
Vogliamo ora effettuare una scomposizione del prodotto sociale complessivo in parti proporzionali alle grandezze di valore in cui si suddivide il capitale merce delle due sezioni. A tal fine, è necessario fissare un sistema di riferimento {βi} ed un valore di riferimento u secondo i criteri visti nel paragrafo 1.1. Nel seguito, quando prenderemo in considerazione le rivoluzioni di valore, manterremo fermo il sistema di riferimento ed analizzeremo le variazioni di u corrispondenti all'aumento della forza produttiva del lavoro sociale. La scomposizione del prodotto complessivo in parti proporzionali, cioè in parti i cui valori rappresentano rispettivamente il capitale costante ed il valore prodotto ex-novo, può ora essere effettuata ponendo:
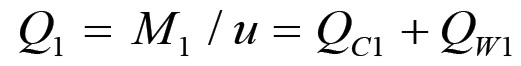 (1.56)
(1.56)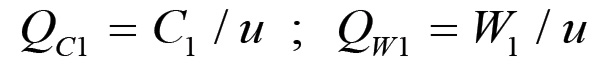 (1.57)
(1.57)con un'analoga definizione per la sezione II. Ora, in virtù dell'equazione (1.54), si ha:
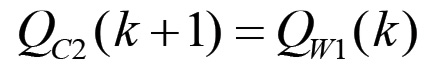 (1.58)
(1.58)in quanto, in assenza di variazioni della forza produttiva del lavoro, deve essere u(k+1) = u(k). Pertanto, arriviamo alla conclusione che la massa della produzione di beni di consumo eguaglierà la parte del prodotto complessivo attuale corrispondente al valore totale prodotto ex-novo. Infatti, dividendo la (1.55) per u si ottiene:
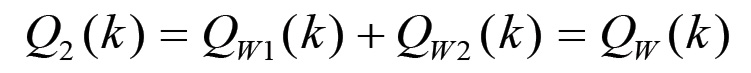 1.59
1.59Vedremo in seguito che la grandezza QW(k) concorre, assieme ad altre variabili, a determinare lo stato del sistema di riproduzione.
1.5 - Riproduzione allargata
Supponiamo ora che il meccanismo di riproduzione rappresentato dal grafo a due nodi di fig. 1.4 sia caratterizzato da valori dei parametri εi minori di uno. In questo caso la configurazione successiva cambierà in accordo alle eq. 1.41 e l'equilibrio potrà essere conservato solo se α1 = α2 , ovvero solo se il saggio di accumulazione è lo stesso per i due nodi del sistema. Si parlerà dunque di riproduzione su scala allargata, per sottolineare il fatto che in questo caso si ha un progressivo allargamento della base produttiva in seguito al processo di accumulazione del capitale. Infatti, mentre nell'ambito della riproduzione semplice tutto il plusvalore prodotto viene destinato al consumo delle classi improduttive, si ha ora che una parte di esso viene trasformata in capitale addizionale, determinando un allargamento della base produttiva della società. In questo caso una parte della produzione QW associata al valore totale prodotto ex novo deve consistere in mezzi di produzione addizionali da impiegare in entrambe le sezioni, per cui deve essere W > M2 e QW > Q2. Se δC(k) = C(k+1) - C(k) è il valore dei mezzi di produzione aggiuntivi, allora l'equazione di consistenza assume la forma:
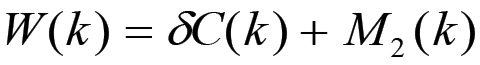 (1.60)
(1.60)Supponiamo ora che la forza produttiva del lavoro sociale rimanga costante nel corso dei vari cicli annuali. Questa assunzione è certamente più vicina alla realtà nel contesto della riproduzione allargata che non in quello della riproduzione semplice, in quanto è principalmente nei periodi di crisi che si verificano cambiamenti significativi della base tecnica del processo lavorativo. In questo caso è possibile in prima approssimazione considerare costante la composizione organica del capitale ed il saggio medio del profitto, per cui i capitali addizionali avranno la stessa composizione del capitale originario:
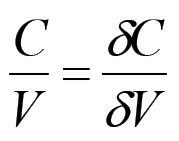 (1.61)
(1.61)Inoltre, se ε è la frazione del plusvalore che la borghesia riserva per proprio il consumo, allora si ha evidentemente:
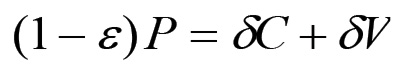 (1.62)
(1.62)Le equazioni (1.61) e (1.62) determinano univocamente le grandezze δC e δV che formano il capitale addizionale che verrà impiegato nel corso dell'anno successivo. Possiamo ora scrivere l'equazione di consistenza (1.60) in forma più esplicita. Nel caso in esame una parte della produzione della sezione I per un valore pari a V1 + δV1 + εP1 si trova sotto forma di mezzi di produzione e deve essere convertita in denaro per consentire l'acquisto di un valore corrispondente in beni di consumo. Questa massa di prodotti può evidentemente essere venduta solo ai capitalisti della sezione II, in quanto la parte restante C1 + δC1 viene venduta e acquistata all'interno della stessa sezione I e completa il fabbisogno di mezzi di produzione dei capitalisti di questa sezione. Per quanto riguarda la sezione II, essa deve convertire in denaro una parte del suo prodotto complessivo, che consiste di beni di consumo, per un valore pari a C2 + δC2, in modo da poter acquistare una massa corrispondente di mezzi di produzione. Questi beni di consumo possono essere venduti solo ai lavoratori impiegati nella sezione I ed ai capitalisti di questa stessa sezione, perché la parte restante V2 + δV2 + εP2 si trova già nella forma di beni di consumo, per cui viene venduta ed acquistata nell'ambito della stessa sezione II ed esaurisce le necessità di consumo dei lavoratori e dei capitalisti di questa sezione. In definitiva, dunque, l'equazione di consistenza prevederà il bilancio nella domanda e nell'offerta di mezzi di produzione e beni di consumo tra le due sezioni.
Questa equazione è l'equazione di Bucharin del meccanismo di riproduzione allargata ed assume pertanto la forma:
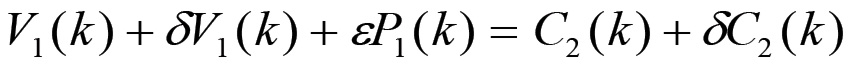 (1.63)
(1.63)Da essa, come ora verifichiamo, può essere ottenuta l'equazione (1.60). Infatti, la (1.63) può essere riscritta come:
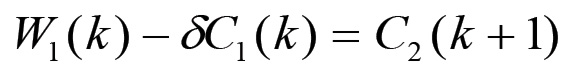 (1.64)
(1.64)Questa equazione corrisponde evidentemente all'analoga equazione di consistenza (1.54) della riproduzione semplice. Ma il secondo membro della (1.64) può ora essere sviluppato come segue:
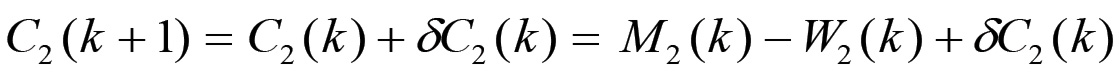
Inserendo questa espressione nella (1.64) si ottiene infine l'equazione di consistenza (1.60). È chiaro dunque che nel caso della riproduzione allargata la sezione I non scambierà con la sezione II una massa di prodotti di valore pari a W1 ma inferiore, in quanto da questa grandezza va detratto il valore δC1 dei mezzi di produzione addizionali che verranno impiegati nella stessa sezione I. Pertanto la (1.58) e la (1.59) non sono valide nel caso di un'estensione della base produttiva. La (1.60) mostra invece che quando la riproduzione si svolge su scala allargata allora QW rappresenta la massa totale di beni di consumo più la massa di mezzi di produzione addizionali destinati all'allargamento della base produttiva. In entrambi i casi, comunque, QW rappresenta la massa di valori d'uso che eccede la riproduzione dei mezzi di produzione attualmente impiegati, ovvero che eccede la riproduzione delle condizioni oggettive della produzione alla scala attuale.
1.6 - Forza produttiva del lavoro
Sia ora n la popolazione operaia impiegata complessivamente in un sistema di riproduzione. Supponiamo inoltre che sia assegnata la durata della giornata lavorativa ed il numero di giornate lavorative che un operaio annualmente impiega, in media, nella produzione. Sia quindi L il numero di giornate di lavoro spese nel corso di un anno da un singolo operaio, cioè il valore da questi prodotto ex-novo nel corso di un ciclo di riproduzione.
È evidente che il valore totale prodotto ex-novo da una popolazione operaia pari ad n sarà:
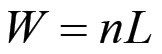 (1.65)
(1.65)Inoltre, in base alla scomposizione del prodotto totale in parti proporzionali si ha che:
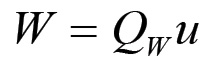 (1.66)
(1.66)Siamo ora in grado di fornire un'espressione quantitativa per la forza produttiva del lavoro sociale. Questa grandezza dovrebbe poter essere determinata indipendentemente dalle categorie e dalle leggi economiche basate sull'applicazione della legge del valore, in quanto si tratta di una variabile determinata dalle modalità tecniche della riproduzione materiale in ogni epoca storica. Da un punto di vista generale, la riproduzione comporta il consumo produttivo di una certa quantità QC di mezzi di produzione e la creazione di una quantità Q di valori d'uso che comprende innanzitutto i mezzi di produzione consumati nell'ambito del processo lavorativo. Con ciò vengono ricreate le condizioni oggettive di partenza per un nuovo ciclo di riproduzione. La restante quantità di valori d'uso prodotta può essere composta esclusivamente da beni di consumo, in particolare quelli destinati alla popolazione lavoratrice, i quali sono gli unici necessari a ricreare le condizioni soggettive di partenza. In questo caso la riproduzione si svolge su scala semplice e la base produttiva resta invariata. Oppure la grandezza Q può contenere una componente addizionale costituita da mezzi di produzione destinati all'allargamento della scala della produzione.
In entrambi i casi il processo di riproduzione comporta la trasformazione di una quantità QC di partenza in una quantità Q > QC data da:
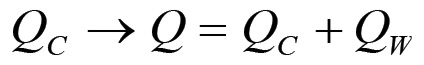 (1.67)
(1.67)È chiaro ora che la forza produttiva del lavoro sarà tanto maggiore quanto maggiore è la differenza tra i valori d'uso prodotti e quelli consumati nella produzione, dunque quanto maggiore risulta essere la grandezza QW = Q - QC. Il secondo fattore che concorre alla formazione di un determinato livello della forza produttiva del lavoro sociale è dato dalla quantità di lavoro umano necessario affinché si verifichi la trasformazione (1.67). Quanto minore è il lavoro erogato nell'ambito del processo di produzione, tanto maggiore sarà la forza produttiva.
Nel caso del modo di produzione capitalistico questo tempo di lavoro viene ad essere rappresentato dal valore prodotto ex novo W, per cui chiamando F la forza produttiva del lavoro sociale avremo che:
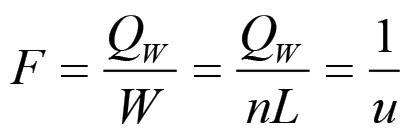 (1.68)
(1.68)Come si vede, la grandezza F viene ad essere inversamente proporzionale al valore di riferimento u, per cui la (1.68) fornisce in effetti un indice della forza produttiva ma non i valori assoluti che via via assume. In ogni caso, la (1.68) stabilisce in modo corretto che ad un aumento generalizzato dei valori individuali delle merci corrisponde una diminuzione della forza produttiva e viceversa.
Consideriamo ora il capitale costante C impiegato annualmente nella riproduzione. Esso, come abbiamo visto, costituisce un invariante della riproduzione semplice. Sia Z il capitale costante che in media viene trasferito nel prodotto finale durante il processo lavorativo da un singolo operaio nell'unità di tempo. Si ha chiaramente che:
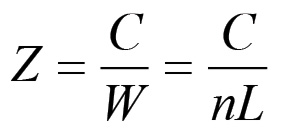 (1.69)
(1.69)La grandezza Z è strettamente collegata alle condizioni tecniche nelle quali avviene la riproduzione. Nel caso della riproduzione semplice il capitale costante C è un invariante, per cui ogni diminuzione del numero di operai in grado di produrre una data massa di valori d'uso QW, dunque ogni aumento della forza produttiva del lavoro associata ad una diminuzione di n, deriva da un aumento di Z, cioè da un aumento del capitale costante su cui opera il singolo operaio, definendo così una sostituzione di lavoro morto a lavoro vivo, di macchine ad uomini. Supponiamo ora che qualsiasi aumento della forza produttiva del lavoro derivi direttamente da un processo di sostituzione di macchine ad uomini, in altri termini che non si verifichino scoperte di nuovi giacimenti ad alta produttività, messa a coltura di nuovi terreni a fertilità superiore a quella dei terreni esistenti, etc. Casi di questo genere comportano evidentemente un aumento di QW, dunque della forza produttiva del lavoro, ma non necessariamente un aumento del capitale costante per operaio. Si tratta d'altra parte di fenomeni sporadici, localizzati nel tempo, la cui influenza consiste semplicemente in deviazioni transitorie e difficilmente quantificabili dalla tendenza generale. Supponiamo dunque che il tasso di aumento della forza produttiva del lavoro sociale sia esattamente uguale al tasso di aumento del capitale costante per operaio. In questo caso è possibile considerare la grandezza Z, che esprime il grado di automazione del processo produttivo, come un indice assoluto del grado di sviluppo delle forze produttive. Se nel corso di un ciclo di riproduzione semplice Z subisce una trasformazione del tipo:
 (1.70)
(1.70)con G > 1, allora anche F dovrà essere soggetto allo stesso tipo di trasformazione:
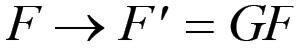 (1.71)
(1.71)Il parametro G definisce pertanto il tasso di sostituzione di macchine ad uomini nell'ambito di una rivoluzione delle modalità tecniche del processo lavorativo.
Essendo C un invariante della riproduzione semplice, la (1.70) implica che la popolazione operaia n deve in questo caso subire una diminuzione data da:
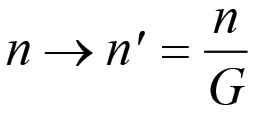 (1.72)
(1.72)Confrontando la (1.71) e la (1.72) con l'espressione (1.68) si vede subito che la grandezza QW, dunque la quantità adimensionale di prodotto corrispondente a W, è un altro invariante della riproduzione semplice. In questo caso l'invarianza va intesa come invarianza rispetto a trasformazioni simultanee di F e Z nell'ambito di una riproduzione su scala costante. È facile vedere che invece, per quanto riguarda la produzione totale, non si ha invarianza rispetto a mutamenti della forza produttiva del lavoro. Infatti, dall'invarianza di C segue che il valore M e la quantità Q della produzione totale si trasformano come:

La proprietà d'invarianza di QW fa si che questa grandezza possa essere convenientemente utilizzata come indice della scala della produzione. Essa infatti rimane costante nell'ambito della riproduzione semplice, anche in presenza di variazioni generalizzate della forza produttiva del lavoro, mentre, come vedremo, varia in proporzione all'allargamento della scala della produzione nel corso dei cicli di riproduzione allargata.
Consideriamo ora una singola unità di prodotto. Vogliamo determinare una scomposizione del suo valore u in aliquote che rappresentano rispettivamente il capitale costante ed il valore ex-novo in essa contenuti.
Poniamo dunque:
 (1.73)
(1.73)L'aliquota del valore unitario u che rappresenta il capitale costante contenuto in un'unità di prodotto è evidentemente data da uc/u; analogamente, la frazione di u che rappresenta il valore ex-novo sarà uw/u. Ora, è chiaro che se Q è la massa totale della produzione, cioè se M = Qu, allora sarà anche: ucQ = C e uwQ = W, per cui si ha:
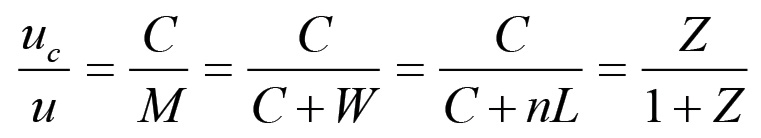 (1.74)
(1.74)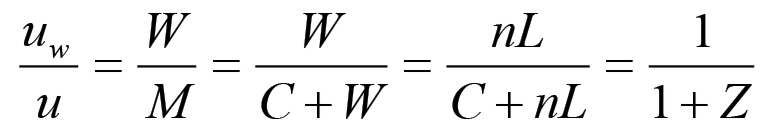 (1.75)
(1.75)Le formule (1.74) e (1.75) determinano uc e uw, in termini percentuali, in funzione della variabile Z e quindi, per il discorso affrontato precedentemente, in funzione della forza produttiva del lavoro; all'aumentare di Z il rapporto uc/u tenderà ad 1, cioè la quota di capitale costante del singolo prodotto tenderà progressivamente al 100% del valore u, mentre uw/u si ridurrà sempre più. Ciò non toglie che, in assoluto, il capitale costante contenuto in un'unità prodotto tenderà a diminuire con l'aumento della forza produttiva del lavoro. Infatti, l'aumento di Z (o, il che è lo stesso, di F) provocherà una progressiva diminuzione nel valore delle materie prime impiegate, come pure un calo nel costo del macchinario. Il seguente esempio mostra come all'aumentare in termini relativi di uc si contrapponga la sua diminuzione in assoluto. Sia dunque C = 2000 gl, QW = 1000 ed L = 100 gl. Se n = 10 allora avremo che:
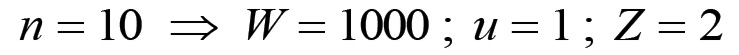
per cui, applicando le formule (1.74) e (1.75) si ha:
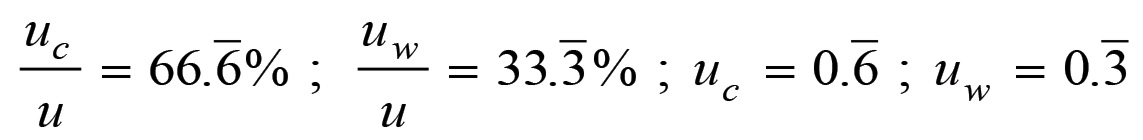
Supponiamo ora che n cali di due unità. Otterremo:
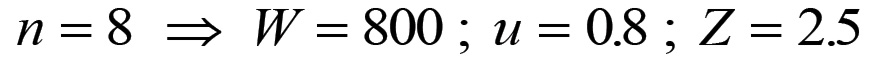
Per cui, procedendo come prima si avrà:
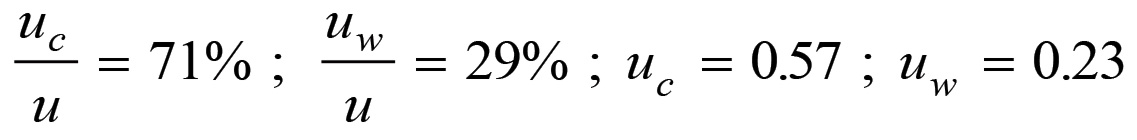
Ciò spiega perché, ad esempio, nel passaggio dai tessuti di cotone a quelli sintetici si osserva contemporaneamente una diminuzione assoluta del capitale costante contenuto in ogni metro di stoffa ed un suo aumento in rapporto al valore unitario del prodotto. In generale, le stesse cause che determinano l'espulsione della forza lavoro dal processo produttivo e la sua sostituzione con macchine automatiche, queste stesse cause generano una diminuzione assoluta nel costo dei mezzi di produzione per unità di prodotto.
1.7 - Capitale variabile e plusvalore
Intendiamo ora occuparci del capitale variabile V anticipato all'inizio di ogni ciclo di riproduzione. In particolare, cercheremo anche in questo caso di collegare le variazioni di questa grandezza alla dinamica delle forze produttive supponendo costante la scala della produzione.
Sia v il valore della forza lavoro; se n è la popolazione operaia complessiva, allora il capitale variabile anticipato è dato da:
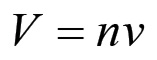 (1.76)
(1.76)Ora, è ben noto che il valore della forza lavoro sta in rapporto inverso, come accade per tutte le merci, con la forza produttiva del lavoro. Poiché quest'ultima è legata in modo biunivoco alla variabile n allora concludiamo che v può essere espressa, in qualche modo, in funzione della popolazione operaia n.
Sia σ la massa di beni di consumo (espressa in uap) corrispondenti al salario; sia cioè:
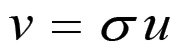 (1.77)
(1.77)Supponiamo inoltre che σ sia costante. Possiamo allora esprimere v in funzione di n ricavando u dalle equazioni (1.65) e (1.66) e sostituendolo nella (1.77):
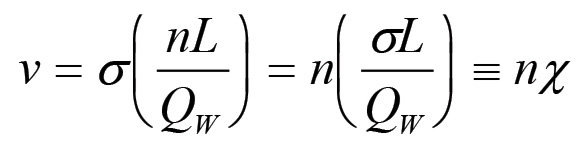 (1.78
(1.78dove abbiamo chiamato χ la costante in parentesi. Questa equazione mostra che il valore della forza lavoro dipende linearmente da n. Ne concludiamo che il capitale variabile V dipenderà dal quadrato di n:
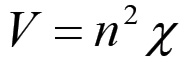 (1.79)
(1.79)Questa espressione non deve stupire: il capitale variabile dipende da n non solo in quanto somma di salari (dunque come prodotto V = nv) ma anche in relazione alla forza produttiva del lavoro, cioè in relazione al fatto che una variazione del numero di operai in grado di produrre la massa di prodotti QW determina una variazione del secondo dei due fattori che formano V, e cioè il valore v della forza lavoro; pertanto V dipenderà doppiamente da n e l'equazione (1.79) ci dice in che modo.
Siamo ora in grado di ricavare un'espressione per la massa di plusvalore prodotta nel corso di un ciclo di riproduzione in relazione a un determinato grado di sviluppo della forza produttiva del lavoro. Poiché P = W - V allora si ha:
 (1.80)
(1.80)Questa formula ha un'importanza fondamentale in quanto mette in luce la contraddizione principale che caratterizza il modo di produzione borghese, e cioè il fatto che la tendenza all'aumento assoluto della forza produttiva del lavoro mediante la sostituzione di macchine ad uomini, mentre da una parte provoca l'aumento del plusvalore estorto al singolo operaio, dunque l'aumento del saggio del plusvalore, dall'altra diminuisce (sulla scala della riproduzione semplice) il secondo dei due fattori che compongono la massa di plusvalore prodotta, cioè il numero di operai. La formula (1.80) mette in evidenza questa contraddizione, poiché in essa il plusvalore è determinato dalla contrapposizione tra due fattori di segno opposto e con dinamiche diverse rispetto alle variazioni di F (o di Z); il primo termine, infatti, diminuisce linearmente all'aumentare di F, mentre il secondo segue un andamento quadratico.
Se consideriamo P come una funzione di F attraverso n, allora la (1.80) ci mostra una parabola (fig. 1.5).
La curva di fig. 1.5 rappresenta tutte le possibili grandezze del plusvalore che la classe borghese può ottenere in un anno, a una data scala della produzione, al variare della popolazione operaia n, dunque in funzione della forza produttiva del lavoro.
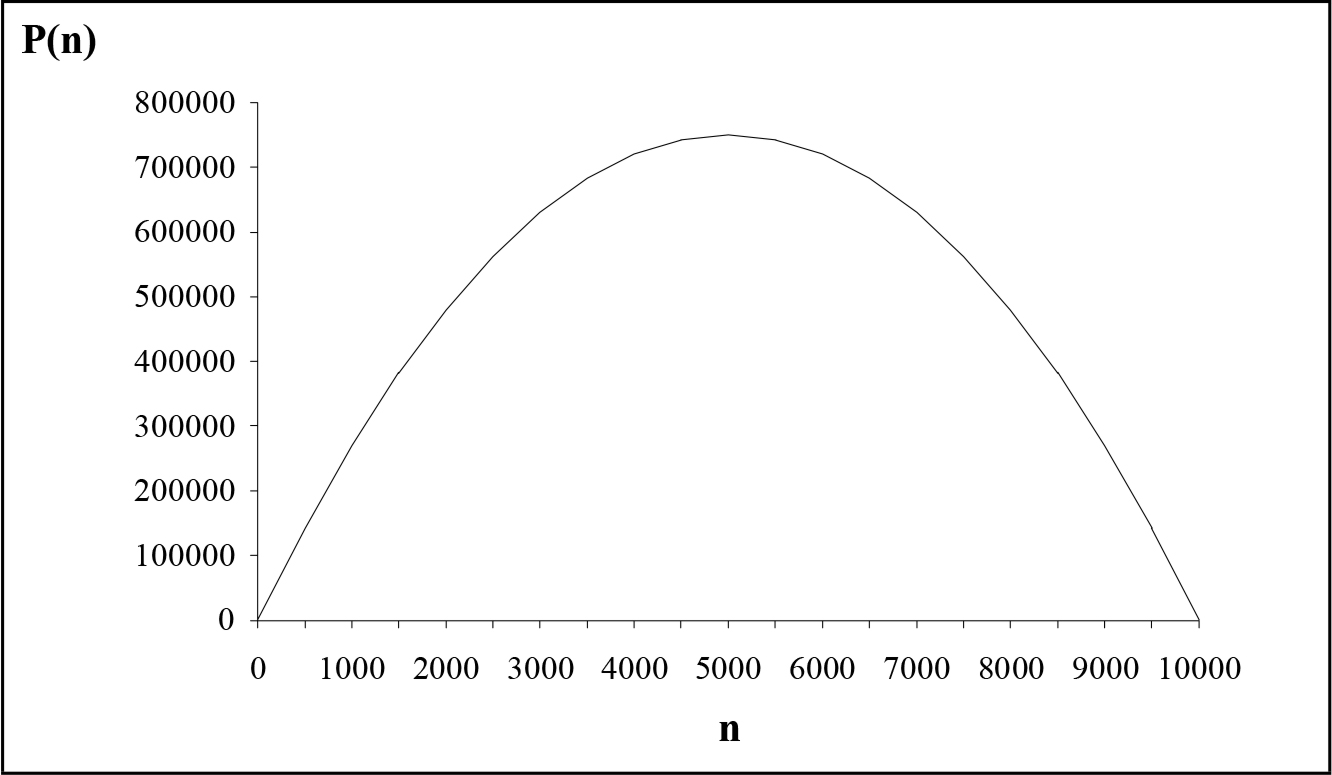 Fig. 1.5 - Parabola del plusvalore nella riproduzione su scala costante
Fig. 1.5 - Parabola del plusvalore nella riproduzione su scala costanteEssa è stata disegnata ponendo L = 300 gl e χ = 0.03. Come si vede, il plusvalore è nullo nel caso (ovvio) di n = 0 e per n = L/χ = 10000. Questo valore di n è significativo; infatti n = L/χ implica che v = nχ = L, e cioè che tutta la giornata lavorativa viene impiegata per la riproduzione della forza lavoro. Si ottiene in questo caso:
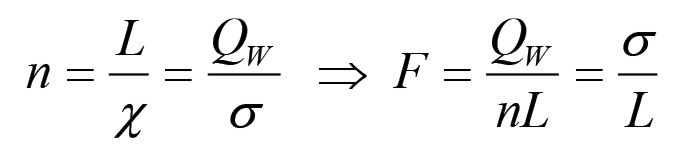 (1.81)
(1.81)Il rapporto σ/L rappresenta dunque il minimo valore che può assumere F; per F = σ/L, infatti, il plusvalore si annulla in quanto la massa QW/n di beni di consumo prodotta per operaio coinciderà con la massa σ di beni di consumo corrispondenti al valore della forza lavoro. In queste condizioni, come pure nel caso puramente teorico F < σ/L, non solo i rapporti di produzione capitalistici sono impossibili, ma diventa pure impossibile qualsiasi forma storica basata sull'esistenza di classi sociali, dunque anche le epoche storiche precedenti alla società borghese e successive alle società primitive. In effetti, per F = σ/L l'intera giornata lavorativa è appena sufficiente alla riproduzione della forza lavoro (ed eventualmente alla riproduzione della famiglia del lavoratore) in quanto le forze produttive non hanno ancora raggiunto il livello minimo necessario per la formazione di pluslavoro, quindi di plusvalore. Una società di questo tipo riuscirebbe a malapena a riprodurre i mezzi di lavoro e le materie prime necessari alla produzione di una massa di beni di consumo che verrebbero interamente consumati dai lavoratori stessi. Inoltre, in queste condizioni non sarebbe nemmeno possibile uscire dal meccanismo della riproduzione semplice, in quanto non verrebbero mai fabbricati mezzi di produzione addizionali. Ne consegue che la stessa popolazione non potrebbe accrescersi.
Lo scenario cambia radicalmente per F > σ/L, cioè per n < L/χ, in quanto diventa possibile, almeno da un punto di vista astratto, la produzione su base capitalistica grazie al fatto che ogni operaio produce ora un plusprodotto dato dalla differenza FL - σ. Inoltre, si osserva un iniziale aumento del pluslavoro complessivo per valori di n progressivamente decrescenti. Ciò avviene per tutti quei valori di F tali che: σ/L < F ≤ 2σ/L, cioè tali che: L/χ < n ≤ L/2χ. Infatti, a partire dal punto n = L/2χ (ovvero per F = 2σ/L) si osserva un'inversione di tendenza, in quanto all'ulteriore diminuzione di n, cioè all'aumento della forza produttiva del lavoro sociale, corrispondono sempre più rapide diminuzioni della massa totale di pluslavoro erogato. Notiamo che per F = 2σ/L si ha che L = 2v, per cui il punto n = L/2χ corrisponde ad una giornata lavorativa ripartita per metà in tempo di lavoro necessario e per l'altra metà in tempo di pluslavoro, quindi, nel caso del modo di produzione borghese, ad un saggio del plusvalore del 100%. Per valori maggiori di F si avranno contemporaneamente masse di pluslavoro complessive più piccole e saggi del pluslavoro in progressivo aumento. Ciò implica che il massimo rendimento del sistema di produzione capitalistico, nel quale come sappiamo la produzione materiale è finalizzata alla produzione di plusvalore, si ha quando il saggio del plusvalore è pari al 100%. È solo in questo caso, infatti, che il plusvalore risulta essere massimo rispetto alla scala della produzione assegnata. Come nel caso di un motore di automobile, nel quale ogni utilizzo al di la della coppia massima determina una diminuzione del rendimento, nel caso della società capitalistica ogni aumento del saggio di sfruttamento del proletariato impiegato nella riproduzione al di la del 100% determinerà inevitabilmente una diminuzione del rendimento associato alla produzione di plusvalore.
Non è ovviamente possibile stabilire il momento esatto della comparsa del modo di produzione capitalistico nell'ambito di questa distribuzione. In altri termini non possiamo determinare in alcun modo quale fosse la ripartizione della giornata lavorativa negli stadi iniziali dell'epoca borghese. Tuttavia, possiamo ritenere che la società antica e quella feudale abbiano portato la forza produttiva del lavoro ad un grado di sviluppo non molto superiore al livello minimo, per cui il vero e proprio balzo in avanti si è avuto solo in tempi relativamente recenti.
Naturalmente, quella che stiamo qui considerando è la scala della riproduzione semplice; l'accumulazione capitalistica trasforma infatti l'eventuale diminuzione del plusvalore in una diminuzione relativa, in quanto l'estensione della scala della produzione che si ha nel meccanismo di riproduzione allargata compensa la diminuzione del plusvalore relativo alla scala della produzione rappresentata da χ. Si tratta, d'altra parte, di vedere fino a che punto è possibile tale meccanismo di compensazione, cosa che sarà oggetto d'indagine nel prossimo capitolo. Si noti, infine, che la grandezza χ, essendo inversamente proporzionale a QW, è un invariante della riproduzione semplice che assume valori tanto minori quanto più è estesa la scala della produzione, per cui può essere utilizzata come un indice indiretto della scala della produzione. Nel seguito, in effetti, troveremo conveniente esprimere le equazioni del processo di accumulazione in termini di χ piuttosto che in funzione dell'indice diretto QW.
1.8 - Il meccanismo della crisi
I concetti introdotti nei paragrafi precedenti possono essere utilizzati per costruire un modello descrittivo del meccanismo generale delle crisi periodiche, anche se per il momento dovranno essere tralasciate le cause che determinano il loro insorgere ad un certo stadio del processo di accumulazione. In effetti, il nostro scopo è innanzitutto quello di inquadrare le crisi ed i successivi periodi di espansione in un modello matematico che tenga conto dello sviluppo storico del modo di produzione capitalistico. Pertanto, ci accontenteremo per ora di considerare solamente i tratti essenziali che caratterizzano i periodi di recessione.
Sono fondamentalmente cinque i fenomeni, la cui concomitanza definisce inequivocabilmente una fase di recessione:
1) Un'interruzione brusca del processo di accumulazione, in altri termini un'interruzione improvvisa di una sequenza di cicli di riproduzione su scala allargata;
2) Un inasprimento della concorrenza, che impone il rinnovamento su larga scala del capitale fisso esistente. Questo rinnovamento non avviene mediante la sostituzione dei vecchi mezzi di lavoro nella loro forma originaria ma bensì mediante l'introduzione di macchine perfezionate. La forma naturale assunta dal capitale fisso nel corso dei periodi di espansione, il fatto che questa forma deve avere una determinata durata media, costituiscono un ostacolo all'introduzione generalizzata di mezzi di lavoro perfezionati. È pertanto nei periodi di crisi, quando la concorrenza si trasforma in vera e propria guerra commerciale, che si assiste al rinnovamento dell'attrezzatura esistente nella maggior parte delle sfere produttive;
3) Una diminuzione generalizzata della popolazione operaia impiegata nel processo di produzione ed un conseguente allargamento dell'esercito industriale di riserva;
4) Una sovrapproduzione più o meno marcata di beni di consumo, che si contrappone alla sovrapproduzione generalizzata del periodo immediatamente precedente alla crisi;
5) Una diminuzione generalizzata nel valore dei prodotti delle diverse sfere di produzione.
Tutti questi fenomeni possono essere inquadrati in un modello di riproduzione semplice che tenga conto di un aumento generale della forza produttiva del lavoro per mezzo della sostituzione di macchine ad uomini. Sia ad esempio L = 300 gl e C = 15000 Mgl (dove 1 Mgl = 1 milione di giornate lavorative). Sia inoltre QW = 75 Muap (cioè 75 milioni di unità adimensionali di prodotto) e σ = 1.5 uap. Infine, supponiamo che al generico ciclo k la popolazione operaia n sia di 25 milioni di unità. Con questi parametri la scala χ della produzione sarà data da: χ = σL/QW = 6∙10-6. Avremo inoltre che:

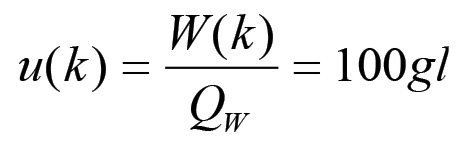
È facile ricavare, a partire da questi valori, i parametri di equilibrio della riproduzione semplice. Infatti, devono valere le seguenti equazioni:
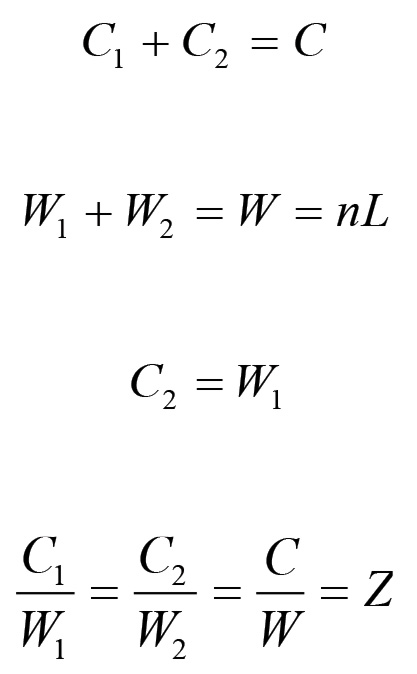
Si noti che la terza equazione di questo sistema è l'equazione di consistenza (1.54) della riproduzione semplice. Risolvendo rispetto al capitale costante ed al valore prodotto ex novo delle due sezioni si ottengono così le seguenti soluzioni:
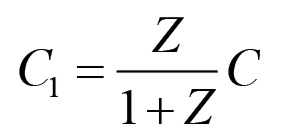 (1.82)
(1.82)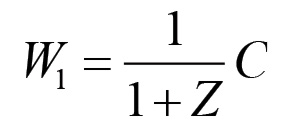 (1.83)
(1.83)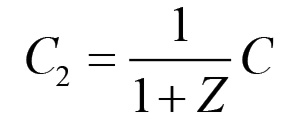 (1.84)
(1.84) (1.85)
(1.85)Pertanto, lo schema assume la forma:

dove tutte le unità si intendono espresse in Mgl. Questo schema esprime una situazione di equilibrio per la quale il valore 15000M1 + 7500M2 = = 22500M posto nella produzione viene completamente realizzato nella circolazione.
Inoltre, una frazione della produzione complessiva pari a W, cioè al valore totale prodotto ex novo, viene completamente assorbita dai rami industriali associati alla produzione di beni di consumo. In questo senso è possibile affermare che nell'ambito della riproduzione semplice i beni di consumo risultano essere sovrapprodotti rispetto alle esigenze del processo di accumulazione.
Vogliamo ora considerare il modo in cui potrebbe effettuarsi il passaggio ad un contesto di riproduzione allargata, dunque ad una nuova fase di espansione. Questa transizione non può chiaramente avvenire in condizioni di equilibrio, in quanto è necessaria una profonda modificazione dei rapporti di valore tra le due sezioni del meccanismo affinché lo schema della riproduzione semplice di Marx si trasformi in uno schema di riproduzione allargata. Di fatto, occorre che una parte del valore prodotto ex-novo nella sezione I consista di mezzi di produzione addizionali. In una prima fase possiamo supporre che la sezione I acquisti e venda al suo interno un maggior numero di macchinari, senza tuttavia impiegare ancora una parte del plusvalore, ma semplicemente utilizzando il risparmio in salari che si determina in seguito ad un aumento della forza produttiva del lavoro.
Supponiamo dunque che si verifichi un incremento degli investimenti nei settori legati alla produzione di macchine perfezionate. Questo è chiaramente legato alla domanda accresciuta di nuovi mezzi di lavoro che si verifica quando la concorrenza costringe i singoli capitalisti a rinnovare le proprie attrezzature. Le cosiddette «ristrutturazioni», che coinvolgono la maggior parte delle aziende nei periodi di crisi, comportano appunto il licenziamento di una parte degli operai e l'acquisto di nuovi macchinari più sofisticati. In questo caso, per tornare allo schema precedente, accade che nell'ambito della sezione I viene acquistata e venduta una massa di mezzi di produzione superiore ai 10000 C1 necessari alla ricostituzione del capitale costante originario di questa sezione. Supponiamo dunque che all'interno della sezione I venga scambiato un valore pari a 10500 Mgl. In questo caso il capitale costante impiegato nella sezione I nel corso dell'anno successivo sarà pari a C1(k+1) = 10500 Mgl, mentre C2(k+1) sarà dato da: C2(k +1) = C - C1(k+1) = 4500 Mgl. Infatti, a conclusione degli scambi intervenuti all'interno della sezione I saranno ancora disponibili mezzi di produzione per un valore pari a 15000 M1 - 10500C1( k+1) = 4500 Mgl. Questo è dunque il valore dei mezzi di produzione che possono essere destinati alla sezione II, per cui i capitalisti di questa sezione potranno vendere agli operai ed ai capitalisti della sezione I beni di consumo per un valore non superiore a 4500 Mgl. Essendo C una costante si ha:
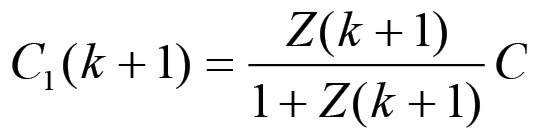
per cui possiamo immediatamente ricavare il valore che assumeranno il capitale costante per operaio Z(k+1), la popolazione operaia n(k+1) ed il valore prodotto ex novo W(k+1) nel corso dell'anno successivo:

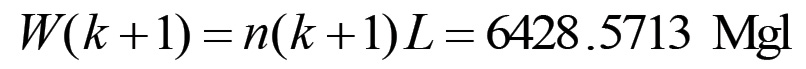
Inoltre, essendo QW e χ degli invarianti, avremo che:
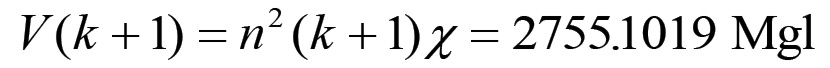
Pertanto, detta Ω = C/V la composizione organica del capitale, il nuovo ciclo di riproduzione partirà con una composizione Ω(k+1) data da:
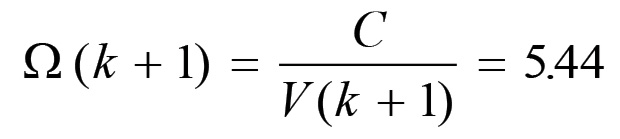
mentre in precedenza avevamo Ω(k) = 4. Con questo valore della composizione organica, la domanda di beni di consumo corrispondenti al salario e provenienti dai lavoratori della sezione II sarà data da:
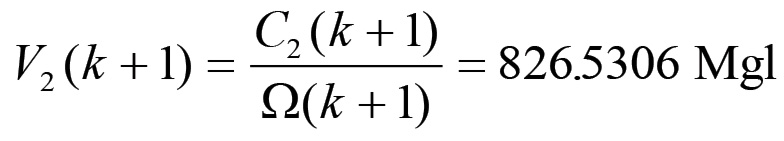
Al termine dell'anno corrente una parte dei capitalisti della sezione II avrà venduto una massa di beni di consumo pari a C2(k+1) + V2(k+1) = 4500 + 826.5306 = 5326.5306 Mgl. Destinatari di questi prodotti sono, in base a quanto detto precedentemente, i capitalisti della sezione I e gli operai di entrambe le sezioni. Notiamo che se ci fosse stato equilibrio tra le due sezioni, il prodotto venduto a queste classi sarebbe stato pari a: C2 + V2 = 6250 Mgl. È facile calcolare il profitto contenuto in questo prodotto. In base ai parametri dello schema si ha infatti che il plusvalore, quando viene realizzato, è una frazione del capitale merce pari a P1/M1 = P2/M2 = P/M = 0.1667, ovvero costituisce il 16.6667% del prodotto. Pertanto, sarebbe stato realizzato un plusvalore pari a 6250 ∙ 0.1667 = 1041.6667 Mgl. Questo valore poteva poi essere utilizzato per acquistare beni di lusso dalla stessa sezione II e ciò avrebbe consentito ai produttori di queste merci di realizzare un plusvalore pari a: 1041.6667 ∙ 0.1667 = 173.6111 Mgl. A sua volta, questo plusvalore sarebbe stato speso consentendo la realizzazione di altre 173.6111 ∙ 0.1667 = 28.94 Mgl, e così via. La serie che si ottiene (1041.6 + + 173.61 + 28.94 + ...) converge evidentemente al plusvalore previsto di 1250 Mgl. Nel caso in esame, invece, la sezione II riesce a vendere inizialmente un prodotto pari a sole 5326.5306 Mgl, per cui è facile controllare che il profitto realizzato sarà di 1065.3061 Mgl. Pertanto, il valore posto nella produzione della sezione II, pari a 7500 M2, ed il valore effettivamente realizzabile nell'ambito della circolazione (5326.5306 + 1065.3061 = 6391.8367 Mgl) non coincideranno e si avrà una sovrapproduzione di beni di consumo pari a 7500 - 6391.8367 = 1108.1633 Mgl.
Esiste qui un'apparente contraddizione tra la grandezza del plusvalore realizzato (1065.3061 Mgl) e l'entità della sovrapproduzione nel settore dei beni di consumo. Infatti, se la sezione II avesse venduto interamente il suo prodotto (pari a 7500 Mgl), avrebbe nello stesso tempo realizzato un profitto pari a 1250 Mgl e ricostituito il capitale anticipato (6250 Mgl). È chiaro dunque che con una vendita effettiva pari a 6391.8367 Mgl, essa riuscirebbe ancora a ricostituire le 6250 Mgl anticipate ma realizzerebbe un profitto pari a sole 6391.8367 - 6250 = 141.8367 Mgl. Come è possibile, invece, che il plusvalore guadagnato dai capitalisti della sezione II sia solo di poco inferiore a 1250 Mgl, e precisamente pari a 1065.3061 Mgl? Per rispondere a questa domanda è necessario approfondire la meccanica degli interscambi che intervengono al termine del k-esimo ciclo.
Suddividiamo logicamente la sezione II in tre sottosezioni, IIA, IIB e IIC, assegnando a ciascuna di esse una certa quota della produzione complessiva della sezione II. Più precisamente, supponiamo che la produzione di queste tre sottosezioni corrisponda rispettivamente al capitale costante, al capitale variabile ed alla massa di plusvalore in cui si scompone il capitale merce della sezione II. In condizioni di equilibrio, detto D = C + V il capitale anticipato, avremmo che la produzione complessiva della sezione II sarebbe ripartita come segue:
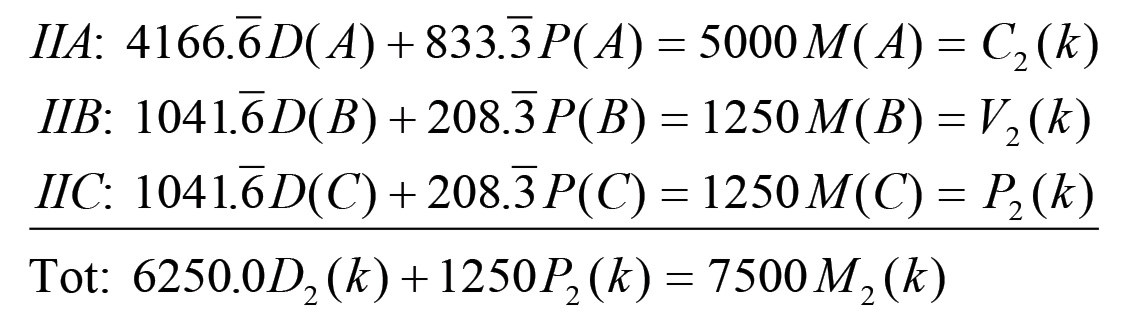
Supponiamo ora che la sottosezione IIA corrisponda al sottoinsieme logico della sezione II che fornisce beni di consumo agli operai ed ai capitalisti della sezione I. Analogamente, supponiamo che le sottosezioni IIB e IIC forniscano rispettivamente mezzi di sussistenza agli operai della sezione II e beni di lusso ai capitalisti della stessa sezione. Nelle condizioni di disequilibrio causate dall'aumento della domanda di mezzi di produzione da parte dei capitalisti della sezione I e dal processo di ristrutturazione, la sottosezione IIA riesce a vendere beni di consumo per un valore complessivo pari a sole 4500 Mgl. D'altra parte, mentre procede alla vendita dei suoi prodotti, essa simultaneamente effettua un anticipo di capitale ed un acquisto di beni di lusso nelle proporzioni determinate dal contenuto in capitale anticipato e plusvalore della merce venduta. Inoltre, l'acquisto di mezzi di produzione e forza lavoro avverrà nelle nuove condizioni tecniche determinate dal rivoluzionamento dei mezzi di lavoro. Ora, ogni capitale merce prodotto nel corso del ciclo di riproduzione attuale ha un contenuto in capitale anticipato pari all'83.3333%, mentre il plusvalore corrisponde al 16.6667% del valore totale. Pertanto, simultaneamente alla vendita del suo prodotto, la sottosezione IIA acquisterà mezzi di produzione e forza lavoro per un valore pari a 0.8333 ∙ 4500 = 3750 Mgl, beni di lusso per un valore pari a 0.1667 ∙ 4500 = 750 Mgl. Al termine degli scambi essa avrà comunque un prodotto invenduto pari a 500 Mgl, dunque perdite per 500 Mgl. Passiamo ora alla sottosezione IIB. Come abbiamo visto, la domanda di beni di consumo proveniente dagli operai della sezione II è 826.5306 Mgl.
Pertanto questo sarà il valore corrispondente al prodotto vendibile della sottosezione IIB. Procedendo come prima si giungerà dunque alla conclusione che questa sottosezione effettuerà un anticipo di capitale pari a 0.8333 ∙ 826.5306 = 688.7755 Mgl per l'acquisto di mezzi di produzione e forza lavoro, ed acquisterà beni di lusso corrispondenti ad un valore pari a 0.1667 ∙ 826.5306 = 137.7551 Mgl. Al termine degli scambi anche questa sottosezione registrerà perdite, in questo caso pari a 1250 - 826.5306 = 423.4694 Mgl. Veniamo infine alla sottosezione IIC. Finora ha venduto ai capitalisti delle altre due sottosezioni beni di lusso per 750 + 137.7551 = 887.7551 Mgl. Con il denaro ricevuto potrà acquistare inizialmente mezzi di produzione e forza lavoro per 0.8333 ∙ 887.7551 = 739.7959 Mgl, nonché beni di lusso (nell'ambito della stessa sottosezione IIC) per un valore pari a 0.1667 ∙ 887.7551 = 147.9592 Mgl. Quest'ultimo valore costituisce una vendita ulteriore, per cui si ha un nuovo anticipo di capitale pari a 0.8333 ∙ 147.9592 = 123.2993 Mgl, ed un nuovo acquisto di beni di lusso per 0.1667 ∙ 147.9592 = 24.6599 Mgl. Reiterando il procedimento si perviene alla fine ad una vendita complessiva pari a 1065.3061 Mgl e quindi ad una perdita pari a 1250 - 1065.3061 = 184.6939 Mgl.
La ripartizione delle perdite fra le tre sottosezioni del settore II può essere determinata analiticamente come segue. Indicando con le perdite subite, si ha che, nel caso delle sottosezioni A e B:
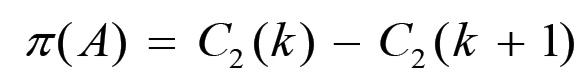 (1.86)
(1.86)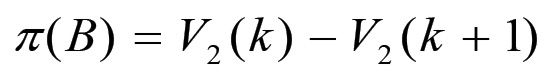 (1.87)
(1.87)Per quanto riguarda la sottosezione C, si ha una perdita iniziale pari a:
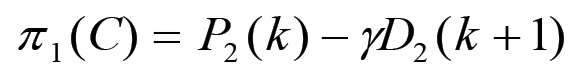 (1.88
(1.88dove γ ≡ P/M nel nostro esempio vale 0.1667. D'altra parte, ogni successiva iterazione del procedimento illustrato in precedenza riduce l'ammontare di questa perdita. Infatti, alla prima iterazione si ha:
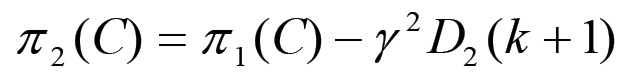
L'ammontare della perdita alla m-esima iterazione è quindi data da:
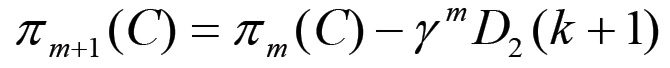 (1.89)
(1.89)La soluzione di questa equazione ricorsiva è immediata. Si ha:
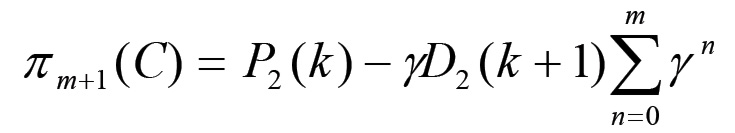 (1.90)
(1.90)La perdita effettiva della sottosezione C può ora essere ottenuta effettuando il passaggio al limite per m→∞. Si ottiene:
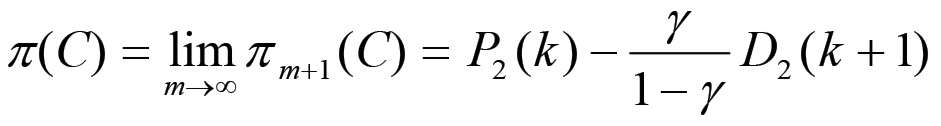 (1.91)
(1.91)Infine, la perdita totale della sezione II sarà data dalla somma delle perdite parziali relative alle tre sottosezioni A, B e C. Utilizzando le eq. (1.86), (1.87) e (1.91) si ottiene dunque:
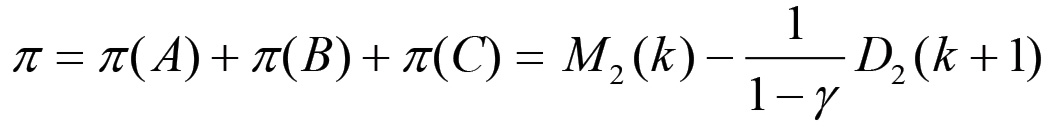 (1.92)
(1.92)Nel caso dell'esempio trattato precedentemente si ha quindi che la perdita complessiva π è pari a 1108.1633 Mgl. Questo risultato conferma il dato già ottenuto in precedenza. Osserviamo ora due cose. Innanzitutto, del capitale merce invenduto solo una frazione pari a 0.8333 ∙ 1108.1633 = 923.4694 Mgl è stata effettivamente pagata dai capitalisti della sezione II sotto forma di capitale anticipato all'inizio del k-esimo ciclo. Pertanto, pur verificandosi una perdita in valore pari a 1108.1633 Mgl, la perdita reale di questi capitalisti è inferiore ed è data dalla quantità di denaro anticipato corrispondente a 923.4694 Mgl. Sottraendo questo valore al profitto realizzato (1065.3061 Mgl) si ottiene un valore pari a 141.8367 Mgl, che è proprio la grandezza ricavata inizialmente sottraendo al capitale merce realizzato (6391.8367 Mgl) il valore del capitale anticipato all'inizio del ciclo (6250 Mgl). Questa considerazione risolve l'apparente contraddizione a cui avevamo accennato. La seconda osservazione riguarda il proletariato ed in particolare i salari. Abbiamo visto che la popolazione operaia, all'inizio del nuovo ciclo cala dai 25 milioni iniziali a 21,428,571 unità, il che provoca un ingrossamento dell'esercito industriale di riserva.
Poiché i capitalisti di entrambe le sezioni all'inizio del nuovo ciclo anticipano in salari un valore pari a V(k+1) = 2755.1019 Mgl, il salario medio per operaio sarà dato da:
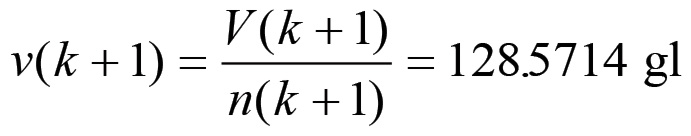
D'altra parte, questi operai sono costretti ad acquistare i propri mezzi di sussistenza al vecchio valore u(k), in quanto le merci prodotte con le nuove tecniche entreranno in circolazione soltanto al termine dell'anno successivo. Gli stessi capitalisti, in effetti, acquistano mezzi di produzione perfezionati al valore u(k) = 100 gl per unità adimensionale di prodotto. Per quanto riguarda gli operai, il salario di 128.5714 gl sarà dunque sufficiente per l'acquisto di una massa di prodotti pari a:
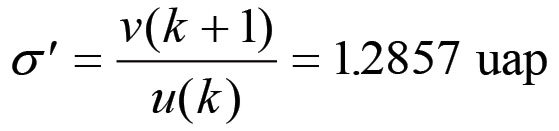
mentre in precedenza il salario reale corrispondeva ad una massa di prodotti pari a σ = 1.5 uap. Pertanto, accanto ai licenziamenti in massa i proletari subiranno una riduzione consistente del salario reale, almeno fino a quando non saranno entrate in circolazione le merci prodotte per mezzo delle nuove tecniche. Inoltre, questa conclusione non viene intaccata dal fatto che nella realtà avvengono più rotazioni in un anno di riproduzione: in ogni caso la diminuzione dei salari precede la diminuzione di valore delle altre merci. Si dispiega qui, nell'ambito delle crisi, una delle contraddizioni più importanti del modo di produzione borghese. Da un lato, infatti, si osserva un restringimento della base del consumo causata dalla compressione dei salari e dal licenziamento di decine di migliaia di lavoratori, dall'altra una massa rilevante di prodotti resta invenduta e giace, priva di valore, nei magazzini. Su questo aspetto della crisi torneremo comunque più avanti.
Torniamo ora alla circolazione delle merci relativa all'esempio trattato precedentemente. La tabella 1.3 riassume i dati ottenuti finora. Le prime tre colonne riportano rispettivamente il valore dei mezzi di produzione acquistati, il capitale variabile anticipato ed il capitale complessivo anticipato all'inizio del ciclo k+1. La quarta colonna riporta invece il profitto realizzato in ciascuna sezione o sottosezione. La quinta colonna si riferisce al valore del capitale merce venduto e, infine, la sesta colonna riporta le perdite subite.
| Sez | C(k+1) | V(k+1) | D(k+1) | P | M | π |
|---|---|---|---|---|---|---|
| I | 10500.0 | 1930.1 | 12430.1 | 2500.0 | 15000.0 | 0 |
| IIA | 3168.1 | 581.9 | 3750.0 | 750.0 | 4500.0 | 500.0 |
| IIB | 581.9 | 106.9 | 688.8 | 137.8 | 826.5 | 423.5 |
| IIC | 750 | 137.8 | 887.8 | 177.6 | 1065.3 | 184.7 |
| II | 4500 | 826.5 | 5326.5 | 1065.3 | 6391.8 | 1108.2 |
Tab. 1.3
Si noti che, tranne che nel caso della sezione I (prima riga della tabella), la somma dei valori riportati nella terza e nella quarta colonna forniscono il valore del capitale merce realizzato, il quale compare in colonna 5. Questa regola non è valida nel caso della sezione I in quanto questi capitalisti hanno un risparmio nell'acquisto di forza lavoro che supera il maggior esborso in mezzi di produzione. Infatti, quest'ultimo è pari a 500 Mgl, mentre il capitale variabile diminuisce dagli originari 2500 Mgl a 1930.1471 Mgl, con un risparmio pari a 569.8529 Mgl. La differenza tra questo risparmio e l'aumento di investimenti determina quindi uno scarto positivo pari a 69.8529 Mgl. Questa somma può dunque essere utilizzata per l'acquisto di beni di lusso aggiuntivi dalla sezione II. In questo modo i capitalisti della sezione I riescono ad acquistare una massa di beni di lusso superiore a quella che sarebbe loro consentito in base al plusvalore disponibile.
Ci resta ora da affrontare l'analisi relativa alla circolazione del denaro. In particolare, ci proponiamo di determinare la quantità massima di circolante necessaria a mediare gli interscambi discussi precedentemente. È chiaro che, nel contesto della circolazione del denaro, tutti i flussi devono configurarsi come movimenti circolari da una sorgente alla sorgente stessa attraverso il mercato. La tabella 1.4 mostra questi flussi riportando, ai diversi stadi del processo di circolazione delle merci, la quantità di denaro (espressa in Mgl) posseduta da parte delle diverse figure economiche che compaiono sul mercato, vale a dire i capitalisti della sezione I, quelli delle tre sottosezioni della sezione II e gli operai.
Inizialmente si suppone che il denaro sia concentrato nelle mani dei capitalisti della sezione I e della sottosezione IIC. Il movimento inizia dai primi con l'acquisto di mezzi di produzione per un valore pari a 10500 Mgl e con l'acquisto di forza lavoro (1930.1471 Mgl, in base ai dati riportati nella tabella 1.4). Poiché i 10500 Mgl vengono spesi nell'ambito della stessa sezione I, il denaro corrispondente a questo valore ritorna nelle mani di questi stessi capitalisti, per cui al passo 1 la somma di denaro da loro posseduta si è ridotta del solo ammontare relativo al capitale variabile anticipato, dunque a 13069.8529 Mgl. Al passo 2 gli operai della sezione I acquistano col denaro ricevuto mezzi di sussistenza dalla sottosezione IIA, la quale si ritrova quindi una somma di denaro corrispondente a 1930.1471 Mgl. Al passo 3 i capitalisti della sezione I acquistano dalla sottosezione IIA beni di lusso per 2569.8529 Mgl, dati dalla somma del plusvalore contenuto nelle loro merci (2500 Mgl) e del risparmio determinato dal processo di ristrutturazione (69.8529 Mgl). A questo punto la massa di denaro in loro possesso è calata ad un livello pari a 10500 Mgl, mentre quella dei capitalisti della sottosezione IIA è aumentata a 4500 Mgl.
Ai passi 4, 5 e 6 questi ultimi utilizzano questo denaro per acquistare in successione mezzi di produzione dalla sezione I (3168.1035 Mgl), forza lavoro (581.8965 Mgl) e beni di lusso dalla sottosezione IIC (750 Mgl). Al successivo passo 7 gli operai della sottosezione IIA acquistano beni di consumo dalla sottosezione IIB, la quale al passo 8 utilizza questo denaro per acquistare mezzi di produzione dalla sezione I. Infine, al passo 9 sono i capitalisti della sottosezione IIC ad acquistare mezzi di produzione per 750 Mgl, per cui la sezione I completa la vendita dei suoi prodotti e ritorna in possesso dell'intera somma messa in circolazione (15000 Mgl).
| Passo | I | IIA | IIB | IIC | Operai |
|---|---|---|---|---|---|
| 0 | 15000.0 | 0 | 0 | 315.3 | 0 |
| 1 | 13069.9 | 0 | 0 | 315.3 | 1930.1 |
| 2 | 13069.9 | 1930.1 | 0 | 315.3 | 0 |
| 3 | 10500.0 | 4500.0 | 0 | 315.3 | 0 |
| 4 | 13668.1 | 1331.9 | 0 | 315.3 | 0 |
| 5 | 13668.1 | 750.0 | 0 | 315.3 | 581.9 |
| 6 | 13668.1 | 0 | 0 | 1065.3 | 581.9 |
| 7 | 13668.1 | 0 | 581.9 | 1065.3 | 0 |
| 8 | 14250.0 | 0 | 0 | 1065.3 | 0 |
| 9 | 15000.0 | 0 | 0 | 315.3 | 0 |
| 10 | 15000.0 | 0 | 0 | 177.6 | 137.8 |
| 11 | 15000.0 | 0 | 137.8 | 177.6 | 0 |
| 12 | 15000.0 | 0 | 30.9 | 177.6 | 106.9 |
| 13 | 15000.0 | 0 | 137.8 | 177.6 | 0 |
| 14 | 15000.0 | 0 | 0 | 315.3 | 0 |
Tab. 1.4
A questo punto il processo riparte dalla sottosezione IIC, la quale ha già acquistato i mezzi di produzione disponibili sul mercato ed ora procede all'acquisto di forza lavoro anticipando un capitale variabile pari a 137.7551 Mgl. Pertanto, al passo 10 essa ha ancora a disposizione una somma di denaro pari a 177.5510 Mgl. Per quanto riguarda gli operai di questa sottosezione, essi possono ora acquistare (passo 11) beni di consumo dalla sottosezione IIB, la quale utilizza a sua volta parte di questo denaro (106.8790 Mgl al passo 12) per anticipare i salari dei suoi lavoratori. Successivamente questi ultimi, al passo 13, acquistano dalla stessa sottosezione IIB i propri mezzi di sussistenza, per cui i capitalisti di questa sottosezione ritornano in possesso della somma iniziale. Questa somma potrà poi essere impiegata per l'acquisto di beni di lusso dalla sottosezione IIC al passo 14.
A questo punto i cicli di compere e vendite della sezione I e delle sottosezioni IIA e IIB sono conclusi, mentre la sottosezione IIC ha venduto finora merci per soli 887.7551 Mgl. La sequenza procede pertanto come descritto in precedenza, attraverso una successione di compere e vendite nell'ambito della stessa sottosezione IIC, fino ad arrivare ad una situazione per la quale il valore realizzato risulta pari a 1065.3061 Mgl.
In definitiva, il modello illustrato precedentemente prevede l'impiego di una massa di circolante pari a 15315.3061 Mgl per la realizzazione di un valore complessivo in merci pari a 15000 + 6391.8367 = 21391.8367 Mgl. Inoltre, questa risulta essere la massima quantità di denaro circolante compatibile con gli interscambi previsti. Essendo la velocità di circolazione definita come il rapporto tra la somma dei prezzi e la massa di circolante, si ottiene una velocità minima pari a:

Questa velocità risulta essere inferiore a quella che avremmo avuto in condizioni di equilibrio. Infatti, in assenza di perturbazioni dovute allo squilibrio tra le due sezioni il capitale merce realizzato sarebbe stato pari a 22500 Mgl mentre, come è facile controllare, la massa di circolante richiesta sarebbe stata di 15416.6667 Mgl. Pertanto, la velocità di circolazione sarebbe stata pari a 22500/15416.6667 = 1.4595.
Il meccanismo della crisi descritto nelle pagine precedenti, pur fornendo una rappresentazione approssimata della realtà, ci consente di comprendere alcuni dei fenomeni più evidenti dei periodi di recessione. Nell'esempio illustrato precedentemente il capitale costante per operaio Z, dunque la forza produttiva del lavoro sociale, aumenta del 16.67%, causando una sovrapproduzione di beni di consumo che si traduce a sua volta in una serie di perdite, ripartite in modo diseguale tra le sottosezioni A, B e C della sezione II. In questo caso la produzione complessiva della società nel corso del ciclo successivo subisce simultaneamente un aumento in quantità ed una diminuzione in valore. Infatti, il capitale merce complessivo che verrà prodotto nel ciclo k+1 sarà dato da:
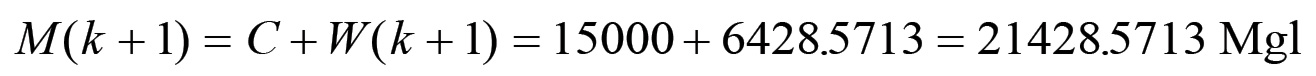
mentre nel corso del ciclo k si aveva: M(k) = 22500 Mgl. Pertanto, la produzione in valore diminuirà del 4.76%. Analogamente, si osserverà una diminuzione generalizzata dei prezzi, corrispondente alla diminuzione dell'indice dei valori dal livello u(k) = 100 gl al livello:
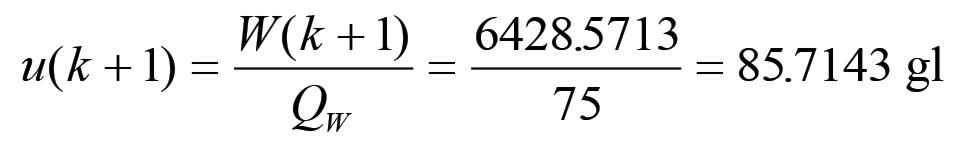
Infine, la produzione complessiva, in quantità, aumenterà dall'indice Q(k) = M(k)/u(k) = 225 Muap all'indice Q(k+1) dato da:
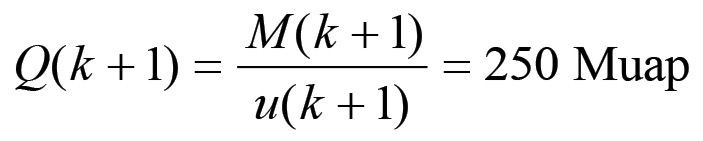
Naturalmente, non tutte le aziende produttive hanno a questo punto introdotto macchine perfezionate. Quelle che l'hanno già fatto riescono per prime ad aumentare la produzione ed il loro mercato diminuendo i prezzi delle merci al di sotto dei prezzi correnti di mercato. Le altre, viceversa, possono solo subire i colpi della concorrenza e, se non chiudono del tutto, sono costrette ad un sottoutilizzo degli impianti esistenti. Complessivamente, però, la grandezza QW che esprime la scala della produzione resta invariata, anche se la sua composizione si modificherà a favore dei mezzi di produzione. Ciò costituisce una premessa fondamentale per l'innesco di una nuova fase di espansione.
Torniamo ora alla questione delle perdite accumulate nell'ambito della sezione II. Esse sono dovute ad un capitale merce invenduto il cui valore virtuale è pari a 1108.1633 Mgl, ma il cui valore di mercato è pari a zero. Fin qui si ha semplicemente una divergenza tra il valore posto nella produzione ed il valore realizzato nella circolazione, dunque uno squilibrio di mercato che determina la chiusura di una parte delle aziende o comunque il rallentamento del loro ritmo di produzione. Questo meccanismo costituisce l'aspetto centrale della crisi, la quale si sviluppa però in una serie di fenomeni collaterali quali la crisi monetaria, il blocco del meccanismo del credito, la crisi della borsa, etc. Un clima di instabilità ed incertezza permea così l'intera società borghese nel corso di questi periodi di recessione. Ma l'aspetto più preoccupante per la borghesia è in ogni caso costituito dal fatto che i massicci licenziamenti e la riduzione dei salari determinano una situazione di povertà o semi-povertà per gran parte della popolazione e una conseguente instabilità del sistema di rapporti di produzione che potrebbe avere conseguenze imprevedibili. È questo il motivo che ha indotto la borghesia a sviluppare una serie di tecniche per controllare il meccanismo della crisi. Il mezzo attraverso il quale viene operato questo controllo è lo Stato. Nel capitolo IV vedremo come il credito, soprattutto quello statale, modifica gli sviluppi della crisi capitalistica.
1.9 - L'accumulazione del capitale
Vogliamo ora studiare l'effetto sulla variabile P di una variazione della scala della produzione. Definiamo un cambiamento della scala della produzione come una trasformazione simultanea delle grandezze n e χ che lasci invariato il prodotto v = nχ, dunque ogni trasformazione del tipo:
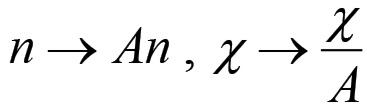 (1.93)
(1.93)dove A è un arbitrario fattore di scala. In particolare, se A > 1 diremo che la trasformazione (1.93) rappresenta un'estensione della scala della produzione e che A è il suo fattore di espansione. La trasformazione (1.93) determina evidentemente una variazione simultanea del numero di operai e della produzione di beni di consumo, tale che il prodotto nχ, il quale rappresenta il valore della forza lavoro, non viene ad essere intaccato. Si noti che nella definizione di χ il termine QW compare al denominatore, per cui dividere χ per A è equivalente a moltiplicare QW per la stessa grandezza A. Ora, moltiplicando simultaneamente n e QW per il fattore A la forza produttiva del lavoro F = QW/nL non cambia, per cui anche v rimane costante e la trasformazione determina semplicemente un ingrandimento oppure un restringimento del sistema di produzione, senza che vengano intaccati i rapporti di valore.
Dimostriamo ora il seguente teorema, di importanza fondamentale per gli sviluppi ulteriori della teoria: detta P(n,χ) la massa di plusvalore che si otterrebbe alla scala della produzione definita da χ con una popolazione operaia n, per ogni trasformazione del tipo (1.93), cioè per ogni cambiamento della scala della produzione con fattore di scala A, il plusvalore P(An,χ/A) relativo alla nuova scala è legato a P(n,χ) dalla relazione:
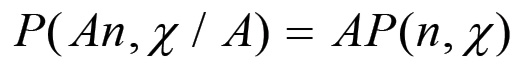 (1.94)
(1.94)Inoltre, la trasformazione non cambia la posizione relativa del punto rappresentativo P (determinata dal grado di sviluppo delle forze produttive) sulla nuova parabola definita dalla (1.94). Il primo punto si dimostra facilmente. Infatti:
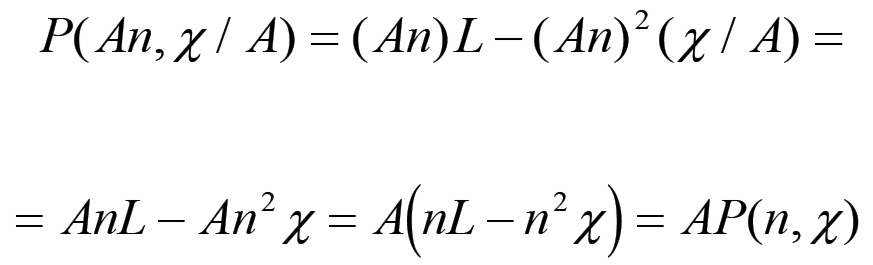
Pertanto il plusvalore viene ad essere moltiplicato per il fattore di scala A. Ora, la posizione relativa del punto rappresentativo sulla parabola può essere definita mediante il rapporto tra la sua ordinata e la sua ascissa, dunque attraverso il rapporto P/n = L - nχ questa grandezza è proprio il plusvalore estorto al singolo operaio e dipende dal prodotto nχ, cioè dal valore della forza lavoro. Ma v è un'invariante sotto trasformazioni del tipo (1.93), per cui il rapporto P/n rimane costante e la posizione relativa del punto invariata. Ciò conclude la dimostrazione del teorema.
Questo teorema è importante in quanto porta alla seguente conclusione: il processo di accumulazione capitalistica, pur determinando una progressiva estensione della scala della produzione, la quale compensa la diminuzione della massa di plusvalore che si verifica a partire dal punto critico F = 2σ/L, non modifica la posizione relativa del punto rappresentativo sulle successive parabole. Pertanto, indipendentemente dal processo di accumulazione, la storia del modo di produzione borghese può essere raffigurata come un progressivo scorrimento verso sinistra del punto rappresentativo lungo la parabola del plusvalore; ogni aumento della forza produttiva del lavoro genera un movimento irreversibile verso sinistra sul diagramma di P, ed ogni estensione della scala della produzione non può modificare le posizioni relative via via raggiunte dal punto rappresentativo. Inoltre, possiamo notare che, quanto più a sinistra è posizionato il punto P, tanto più repentina sarà la diminuzione del plusvalore che seguirà ad un aumento di F, tanto maggiore dovrà essere dunque il fattore di espansione A necessario per compensare tale diminuzione. I grafici rappresentati in fig. 1.6 mostrano l'effetto combinato di un aumento di F e di un'estensione della scala della produzione.
Consideriamo ora il capitale costante per operaio Z = C/nL; abbiamo visto che questa grandezza costituisce un indicatore del grado di sviluppo delle forze produttive, per cui ci aspettiamo che sia invariante sotto trasformazioni del tipo (1.93). Affinché ciò avvenga è necessario che il capitale costante C si trasformi come n: C→AC. L'invarianza di Z e v sotto trasformazioni di scala conduce alla seguente proposizione: ogni funzione delle sole variabili Z e v è invariante rispetto a cambiamenti della scala della produzione.
Comprenderemo tra breve l'importanza di questa conclusione. Siamo ora in grado di determinare i rapporti fondamentali di valore definiti dal saggio del plusvalore, dal saggio del profitto e dalla composizione organica del capitale in funzione della forza produttiva del lavoro.
 Fig. 1.6 - Effetto combinato di un aumento della forza produttiva del lavoro e di un'estensione della scala della produzione.
Fig. 1.6 - Effetto combinato di un aumento della forza produttiva del lavoro e di un'estensione della scala della produzione.Indicando come sempre con S, τ e Ω queste tre grandezze si ha:
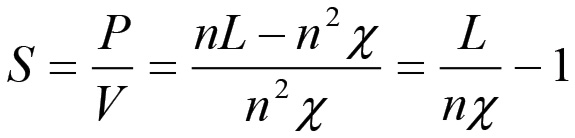 (1.95)
(1.95)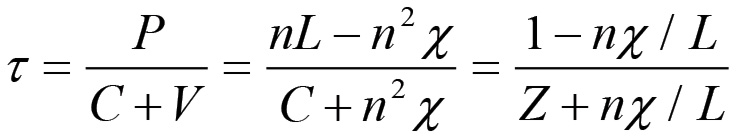 (1.96)
(1.96)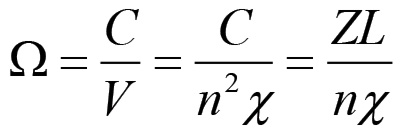 (1.97)
(1.97)Osserviamo ora queste tre formule; possiamo notare che in esse le variabili n e χ compaiono sempre accoppiate tramite il prodotto nχ, per cui le funzioni S, τ e Ω vengono a dipendere dalle sole variabili Z e v. Ne concludiamo che i tre rapporti fondamentali di valore non dipendono dalla scala della produzione e possono essere pertanto studiati anche nell'ambito della riproduzione semplice. Vale dunque la seguente proposizione: ogni conclusione riguardante il saggio del plusvalore, il saggio del profitto o la composizione organica del capitale, tratta facendo riferimento allo schema di riproduzione semplice, risulta valida anche in uno schema di riproduzione allargata.
Ora, da un primo e superficiale studio della formula (1.96) risulta chiaramente che il saggio del profitto τ segue un andamento simile (ma non uguale) a quello che caratterizza la curva P = P(n) del plusvalore, poiché anche in questo caso si ha un massimo della curva τ = τ(n) in corrispondenza ad un certo valore della forza produttiva F. Pertanto, a parte una fase iniziale caratterizzata dall'aumento di τ, la storia del modo di produzione borghese presenta, da un certo punto in poi, una diminuzione progressiva del saggio del profitto. Ciò costituisce evidentemente una dimostrazione della legge sulla caduta tendenziale del saggio del profitto senza l'ipotesi semplificativa di un saggio costante del plusvalore. Questa legge resta dunque valida malgrado il progressivo aumento del saggio del plusvalore S. D'altra parte, osservando le formule (1.95) e (1.97), si vede subito che Ω aumenta più rapidamente di S.
Poiché il saggio del profitto può essere espresso in termini di S e Ω come:
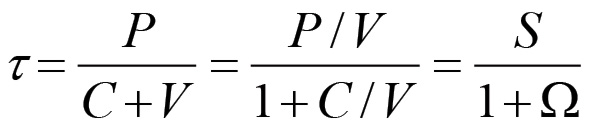 (1.98)
(1.98)allora è evidente che, da un certo punto in poi, questa grandezza deve iniziare a calare. La (1.96) consente pertanto di stabilire esattamente il punto a partire dal quale inizia la caduta tendenziale del saggio medio del profitto.
Nel prossimo capitolo prenderemo in considerazione lo sviluppo storico del processo di accumulazione, in modo da comprendere come e perché la caduta tendenziale del saggio del profitto determina, a partire da un certo grado di sviluppo delle forze produttive, lo stravolgimento di quella stessa dinamica di cui costituisce il prodotto.

Dinamica dei processi storici Volume I
Teoria dell'accumulazione
Quaderni di n+1.
Una formalizzazione spinta del sistema di riferimento marxista. In questo volume gli schemi di Marx vengono affiancati da una ulteriore dimostrazione poggiante su potenti strumenti matematici che confermano il carattere transitorio del capitalismo.

 n+1
n+1